Electron shell
The atomic shell or electron shell consists of the electrons bound by an atomic nucleus and usually surrounding it to a distance of the order of 10-10 m (atomic radius). The nucleus and the atomic shell together form the atom, with the nucleus having a diameter 20,000 to 150,000 times smaller than the shell, depending on the chemical element, but containing 99.95% to 99.98% of the total atomic mass. The properties of the atom that are accessible from the outside are therefore, apart from the mass, almost exclusively determined by the shell. These include, in addition to the size of the atom, its various possible types of chemical bonding, the possibilities of forming a molecule or a crystalline solid, the emission and absorption of electromagnetic radiation of certain wavelengths in the infrared, visible light, ultraviolet and X-ray ranges. Atomic physics, which is largely concerned with these phenomena, is therefore largely a physics of the atomic shell.
The number 


Various atomic models have been developed for the structure of the electron shell. The first model, which was very successful in parts, was the Bohr atomic model (after Niels Bohr) in 1913, which is still the basis of many popular representations today. From 1925 onwards, it was replaced by the much more comprehensive and precise quantum mechanical atomic models, which still form the theoretical basis of atomic physics today.
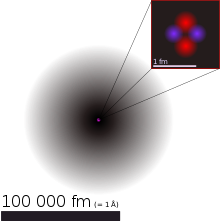
The electron-shell (grey) of the helium-atom (enlarged about 400 million times) with atomic nucleus (red dot, again enlarged 100 times). The nucleus schematically is shown upside right, once more enlarged by 40-fold. In reality it is sphere-shaped.
Properties of the entire hull
Binding energy
The atomic shell consists of electrons that are bound to the positive atomic nucleus due to their negative electric charge. The total binding energy of the 

![{\displaystyle 13{,}6\;Z^{7/3}\left[1+{\tfrac {1}{2}}(1-Z^{-1/3})^{2}\right]\,\mathrm {eV} }](https://www.alegsaonline.com/image/4aa95d452cc6ff44ea3d8db647e04073b6864131.svg)







In the simplest model of the atomic shell, a somewhat stronger increase of the binding energy per electron like 








Shape and size
The atomic shell does not have a sharply defined surface, but shows an approximately exponential decrease in electron density in the outer region. The size and shape of the atom are usually defined by a surface area that is as small as possible and contains a large part (e.g. 90 %) of the total electron density. This surface area is approximately spherical in most cases, except for atoms chemically bound in a molecule or some crystal lattices, or after special preparation in the form of a Rydberg atom. The whole shell can oscillate against the nucleus, the frequency being around 1017Hz (or excitation energy around 100 eV) for the xenon atom with 54 electrons, for example.
Due to the fuzzy edge of the atomic shell, the size of the atoms is not unambiguously fixed (see atomic radius). The tabulated values are obtained from the bond length, which is the most energetically favorable distance between the atomic nuclei in a chemical bond. Overall, increasing atomic number shows a roughly periodic variation in atomic size, which agrees well with the periodic variation in chemical behavior. In the periodic table of the elements, it is generally true that within a period, i.e. a line of the system, a certain shell is filled up. From left to right the size of the atoms decreases, because the nuclear charge increases and therefore all shells are more strongly attracted. When a certain shell is filled with the strongly bound electrons, the atom belongs to the noble gases. With the next electron the occupation of the shell with next bigger energy begins, which is connected with a bigger radius. Within a group, i.e. a column of the periodic table, the size therefore increases from top to bottom. Accordingly, the smallest atom is the helium atom at the end of the first period with a radius of 32 pm, while one of the largest atoms is the cesium atom, the first atom of the 5th period. It has a radius of 225 pm.
Density
Contrary to many popular representations, the atomic shell is by no means an essentially empty space. Rather, the average electron density of the shell varies between 0.01 and 0.1 kg/m3 depending on the element. For comparison, air has this density at a pressure between 10 and 100 mbar. The idea of the envelope as an (almost) empty space would result if at any given time the electrons were at specific locations in space as nearly perfect mass points. However, the idea of such localized electrons within the atom is inadmissible according to quantum mechanics.
Angular momentum
The atomic shell of a free atom has a certain angular momentum in each energy level. It is usually 









Experimental methods for the study of the atomic shell
The size of the atomic shell is determined primarily within the framework of kinetic gas theory and crystal structure analysis (see atomic radius). Methods for the elucidation of the structure of the atomic shell are summarized under the term methods of atomic physics. They are presented in detail in their own articles. Typical examples are (although the list is by no means exhaustive):
- X-ray photoelectron spectroscopy (XPS): The absorption of a quantum of high-energy X-rays in the photoelectric effect produces a free electron with a kinetic energy that is the difference between the energy of the absorbed quantum and the binding energy that the electron previously had in the shell. Electrons with the lowest kinetic energy had the highest binding energy
and come from the K shell. After that, at a binding energy of about
come the three closely spaced binding energies of the L shell, and so on. The energetic shell structure of the shell, starting from about
including the splitting according to the structure after jj-coupling, is clearly shown.
- Atomic emission spectrometry and atomic absorption spectrometry: The spectral investigation of the electromagnetic radiation emitted or absorbed by atomic shells with respect to their wavelength, especially in the visible light, ultraviolet, infrared ranges, provides information about the energy distances of the different energy levels of the atom. In many cases these energies can be interpreted by the change of only one electron from one orbital to another (luminous electron). This has contributed significantly to the study of the atomic shell and thus to the discovery of quantum mechanics. Emission and absorption spectra are characteristic of the element in question and are used for chemical analysis. Therefore, optical spectroscopy is the oldest of the methods mentioned here. Other important results of the measurements are the intensity (especially in the ratio of different spectral lines) and polarization of the radiation.
- X-ray spectroscopy: Like optical spectroscopy above, but in the energy range of X-rays and therefore differently built spectrometers. The strength of the absorption increases abruptly with increasing energy of the X-ray quanta each time the binding energy of an orbital is exceeded (absorption edge). This was the first experimental evidence of the magnitude and quantization of the binding energies of the internal electrons in the atom. The emission of X-rays triggered by absorption shows a simple line spectrum characteristic of each element (characteristic X-ray, X-ray fluorescence analysis). The fact that it only arises when an inner electron has previously been knocked out was the first indication that a weaker bound electron can only jump to a lower level if there is a vacancy there ("hole state").
- Auger electron spectroscopy (AES): An excited atom can emit an electron instead of a photon (Auger effect) if the excitation energy makes this possible. In that case, the Auger effect is generally even the more common one. In detail it is based on the fact that in a level with high binding energy one electron is missing (hole state) and that two weaker bound electrons of the shell make a collision by means of their electrostatic repulsion, so that one of them fills the hole state and the gained energy is sufficient for the other to leave the atom. The energy and intensity of the emitted electrons is measured. These are also element-specific and are used for chemical analysis of the thinnest layers.
- Electron scattering: Investigation of the electrons emitted from atomic shells after the impact of a high-energy electron with respect to their energy and intensity.
Questions and Answers
Q: What is an electron shell?
A: An electron shell, or main energy level, is the part of an atom where electrons are found orbiting the atom's nucleus.
Q: How many electrons can be in a certain shell?
A: The number of electrons that can be in a certain shell is equal to 2n2.
Q: What does the Bohr model state about electrons?
A: The Bohr model states that electrons orbit the nucleus at certain distances so that their orbits form "shells".
Q: Who presented this term?
A: This term was presented by Niels Henrik David Bohr.
Q: What makes up the electron configuration of an atom?
A: Electron shells make up the electron configuration of an atom.
Q: Are all atoms made up of one or more electron shells?
A: Yes, all atoms have one or more electron shells.
Q: Do all electron shells have varying numbers of electrons?
A: Yes, all electron shells have varying numbers of electrons.
Search within the encyclopedia