Dot product

This article deals with the multiplication of two vectors whose result is a scalar. For the multiplication of vectors with scalars whose result is a vector, see scalar multiplication.

The scalar product (also inner product or dot product) is a mathematical connection that assigns a number (scalar) to two vectors. It is the subject of analytical geometry and linear algebra. Historically, it was first introduced in Euclidean space. Geometrically, one calculates the scalar product of two vectors ${\vec {a}}$ and ${\vec {b}}$ according to the formula

${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\,\cos \sphericalangle ({\vec {a}},{\vec {b}}).$

Here $|{\vec {a}}|$ and $|\vec b|$ denote the lengths (amounts) of the vectors respectively. $\cos \sphericalangle(\vec a, \vec b) = \cos \varphi$ $\varphi$ denotes the cosine of the angle φ \varphi enclosed by the two vectors. The scalar product of two vectors of given length is thus zero if they are perpendicular to each other and maximum if they have the same direction.

In a Cartesian coordinate system, the scalar product of two vectors ${\vec {a}}=(a_{1},a_{2},a_{3})$ and is calculated ${\vec {b}}=(b_{1},b_{2},b_{3})$ as

${\vec {a}}\cdot {\vec {b}}=a_{1}\,b_{1}+a_{2}\,b_{2}+a_{3}\,b_{3}.$

Knowing the Cartesian coordinates of the vectors, one can use this formula to calculate the scalar product and then the formula from the previous paragraph to calculate the angle φ $\varphi =\sphericalangle ({\vec {a}},{\vec {b}})$ between the two vectors by $\varphi$ solving for φ

$\varphi =\arccos {\frac {{\vec {a}}\cdot {\vec {b}}}{|{\vec {a}}||{\vec {b}}|}}$

In linear algebra, this concept is generalised. There, a scalar product is a function that assigns a scalar to two elements of a real or complex vector space, more precisely a (positive definite) Hermitian sesquilinear form, or more specifically, in the case of real vector spaces, a (positive definite) symmetric bilinear form. In general, a scalar product is not defined a priori in a vector space. A space together with a scalar product is called an inner product space or prehilver space. These vector spaces generalise Euclidean space and thus enable the application of geometric methods to abstract structures.

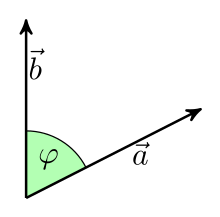
The scalar product of two vectors in Euclidean visual space depends on the length of the vectors and the included angle.

In Euclidean space

Geometric definition and notation

Vectors in three-dimensional Euclidean space or in the two-dimensional Euclidean plane can be represented as arrows. Arrows that are parallel, of the same length and oriented in the same way represent the same vector. The scalar product $\vec a \cdot \vec b$ two vectors ${\vec {a}}$ and ${\vec {b}}$ is a scalar, i.e. a real number. Geometrically it can be defined as follows:

Let $a = |\vec a|$ and $b = |\vec b|$ the lengths of the vectors ${\vec {a}}$ and ${\vec {b}}$ and let φ $\varphi = \sphericalangle(\vec a, \vec b)$ the ${\vec {b}}$ angle enclosed by ${\vec {a}}$ and then

$\vec a \cdot \vec b = |\vec a| \, |\vec b| \, \cos \sphericalangle (\vec a, \vec b) = a\, b \, \cos \varphi.$

As with normal multiplication (but less often than there), if it is clear what is meant, the multiplication sign is sometimes omitted:

${\vec {a}}\cdot {\vec {b}}={\vec {a}}\,{\vec {b}}$

Instead of one occasionally writes ${\vec {a}}\cdot {\vec {a}}$ this case $\vec a\,^2.$

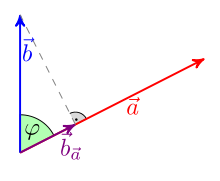
Other common notations are $\vec a \circ \vec b,\ \vec a \bullet \vec b$ and ⟨ $\langle \vec a, \vec b \rangle.$

Illustration

To visualise the definition, consider the orthogonal projection $\vec b_{\vec a}$ the vector ${\vec {b}}$ onto the ${\vec {a}}$ direction determined by and set

$b_{a}={\begin{cases}|{\vec {b}}_{\vec {a}}|&{\text{falls }}{\vec {a}},{\vec {b}}_{\vec {a}}{\text{ gleichorientiert}}\\-|{\vec {b}}_{\vec {a}}|&{\text{falls }}{\vec {a}},{\vec {b}}_{\vec {a}}{\text{ entgegengesetzt orientiert}}\end{cases}}$

Then $b_{a}=b\cos \varphi$ and for the scalar product of ${\vec {a}}$ and ${\vec {b}}$ holds:

$\vec a \cdot \vec b = a b_a$

This relationship is sometimes also used to define the scalar product.

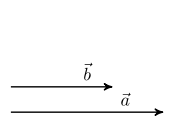
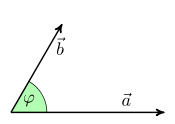
Examples

In all three examples $| \vec a | = 5$ and $| \vec b | = 3$ . The scalar products are obtained using the special cosines $\cos 0^\circ = 1$ $\cos 60^\circ = \tfrac{1}{2}$ and $\cos 90^\circ = 0$ :

${\vec {a}}$ and ${\vec {b}}$ equidirectional
${\vec {a}}\cdot {\vec {b}}=5\cdot 3\cdot \cos 0^{\circ }=15$

${\vec {a}}$ and ${\vec {b}}$ at an angle of 60°.
${\vec {a}}\cdot {\vec {b}}=5\cdot 3\cdot \cos 60^{\circ }=7{,}5$

${\vec {a}}$ and ${\vec {b}}$ orthogonal
${\vec {a}}\cdot {\vec {b}}=5\cdot 3\cdot \cos 90^{\circ }=0$

In Cartesian coordinates

If one introduces Cartesian coordinates in the Euclidean plane or in Euclidean space, each vector has a coordinate representation as a 2- or 3-tuple, which is usually written as a column.

In the Euclidean plane one then obtains for the scalar product of the vectors

and $\vec a = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ $\vec b = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$

the representation

$\vec a \cdot \vec b = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \cdot \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} = a_1 b_1 + a_2 b_2.$

For the canonical unit vectors $\vec e_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$ and $\vec e_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$ namely:

${\vec {e}}_{1}\cdot {\vec {e}}_{1}=1,\ {\vec {e}}_{1}\cdot {\vec {e}}_{2}={\vec {e}}_{2}\cdot {\vec {e}}_{1}=0$ and ${\vec {e}}_{2}\cdot {\vec {e}}_{2}=1$

From this follows (anticipating the properties of the scalar product explained below):

${\begin{aligned}{\vec {a}}\cdot {\vec {b}}&=(a_{1}\,{\vec {e}}_{1}+a_{2}\,{\vec {e}}_{2})\cdot (b_{1}\,{\vec {e}}_{1}+b_{2}\,{\vec {e}}_{2})\\&=a_{1}b_{1}\,{\vec {e}}_{1}\cdot {\vec {e}}_{1}+a_{1}b_{2}\,{\vec {e}}_{1}\cdot {\vec {e}}_{2}+a_{2}b_{1}\,{\vec {e}}_{2}\cdot {\vec {e}}_{1}+a_{2}b_{2}\,{\vec {e}}_{2}\cdot {\vec {e}}_{2}\\&=a_{1}b_{1}+a_{2}b_{2}\end{aligned}}$

In three-dimensional Euclidean space, one obtains accordingly for the vectors

and $\vec a = \begin{pmatrix} a_1 \\ a_2 \\a_3 \end{pmatrix}$ $\vec b = \begin{pmatrix} b_1 \\ b_2 \\b_3 \end{pmatrix}$

the representation

$\vec a \cdot \vec b = \begin{pmatrix} a_1 \\ a_2\\ a_3 \end{pmatrix} \cdot \begin{pmatrix} b_1 \\ b_2 \\b_3 \end{pmatrix} = a_1 b_1 + a_2 b_2 + a_3 b_3.$

For example, the scalar product of the two vectors is calculated as follows

and $\vec a = \begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}$ $\vec b = \begin{pmatrix}-7 \\ 8 \\ 9 \end{pmatrix}$

as follows:

$\vec a \cdot \vec b = 1 \cdot (-7) + 2 \cdot 8 + 3 \cdot 9 = 36$

Properties

From the geometric definition it follows directly:

If ${\vec {a}}$ and are ${\vec {b}}$ parallel and equally oriented ( $\varphi = 0^\circ$ ), the following holds

$\vec a \cdot \vec b = a b.$

In particular, the scalar product of a vector with itself gives the square of its length:

$\vec a \cdot \vec a = a^2$

If ${\vec {a}}$ and are ${\vec {b}}$ parallel and oppositely oriented ( $\varphi = 180^\circ$ ), the following applies

${\vec {a}}\cdot {\vec {b}}=-ab.$

If ${\vec {a}}$ and ${\vec {b}}$ are orthogonal ( $\varphi = 90^\circ$ ), then

$\vec a \cdot \vec b = 0.$

If $\sphericalangle(\vec a, \vec b)$ an acute angle, then $\vec a \cdot \vec b > 0.$
If $\sphericalangle(\vec a, \vec b)$ an obtuse angle, then $\vec a \cdot \vec b < 0.$

As a function that assigns to $\vec a \cdot \vec b$ each ordered pair $(\vec a, \vec b)$ of vectors the real number , the scalar product has the following properties expected of multiplication:

It is symmetrical (commutative law):

$\vec a \cdot \vec b = \vec b \cdot \vec a$ for all vectors ${\vec {a}}$ and ${\vec {b}}$

It is homogeneous in each argument (mixed associative law):

$(r \vec a) \cdot \vec b = r\, (\vec a \cdot \vec b) = \vec a \cdot (r \vec b)$ for all vectors ${\vec {a}}$ and ${\vec {b}}$ and all scalars $r\in \mathbb {R}$

It is additive in each argument (distributive law):

$\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec b + \vec a \cdot \vec c$ and

$(\vec a + \vec b) \cdot \vec c = \vec a \cdot \vec c + \vec b \cdot \vec c$ for all vectors $\vec a,$ ${\vec {b}}$ and $\vec c.$

Properties 2 and 3 can also be combined: The scalar product is bilinear.

The designation "mixed associative law" for the 2nd property clarifies that here a scalar and two vectors are linked in such a way that the brackets can be interchanged as in the associative law. Since the scalar product is not an inner linkage, a scalar product of three vectors is not defined, so the question of true associativity does not arise. In the expression $({\vec {a}}\cdot {\vec {b}})\,{\vec {c}}$ only the first multiplication is a scalar product of two vectors, the second is the product of a scalar with a vector (S-multiplication). The expression represents a vector, a multiple of the vector $\vec c.$ On the other hand, the expression $\vec a \, (\vec b \cdot \vec c)$ represents a multiple of ${\vec {a}}$ In general, therefore

$({\vec {a}}\cdot {\vec {b}})\,{\vec {c}}\neq {\vec {a}}\,({\vec {b}}\cdot {\vec {c}}).$

Neither the geometric definition nor the definition in Cartesian coordinates is arbitrary. Both follow from the geometrically motivated requirement that the scalar product of a vector with itself is the square of its length, and the algebraically motivated requirement that the scalar product satisfies properties 1-3 above.

Amount of vectors and included angle

With the help of the scalar product it is possible to calculate the length (the amount) of a vector from the coordinate representation:

For a vector $\vec a = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ of the two-dimensional space, the following applies

$|{\vec {a}}|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}}}.$

The Pythagorean theorem can be recognised here. In three-dimensional space the following applies accordingly

$|{\vec {a}}|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}}}.$

By combining the geometric definition with the coordinate representation, one can calculate the angle enclosed by two vectors from their coordinates. From

$\vec a \cdot \vec b = |\vec a| \, |\vec b| \, \cos \sphericalangle (\vec a, \vec b)$

follows

$\cos \sphericalangle ({\vec {a}},{\vec {b}})={\frac {{\vec {a}}\cdot {\vec {b}}}{|{\vec {a}}|\,|{\vec {b}}|}}.$

The lengths of the two vectors

and $\vec a = \begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}$ $\vec b = \begin{pmatrix}-7 \\ 8 \\ 9 \end{pmatrix}$

therefore amount to

$|{\vec a}|={\sqrt {1^{2}+2^{2}+3^{2}}}={\sqrt {14}}\approx 3{,}74$ and $|\vec b| = \sqrt{(-7)^2+8^2+9^2} = \sqrt{194} \approx 13{,}93.$

The cosine of the angle enclosed by the two vectors is calculated to be

$\cos \sphericalangle ({\vec {a}},{\vec {b}})={\frac {36}{{\sqrt {14}}\cdot {\sqrt {194}}}}\approx 0{,}691.$

Thus $\sphericalangle ({\vec {a}},{\vec {b}})\approx 46{,}3^{\circ }.$

Orthogonality and orthogonal projection

→ Main article: Orthogonality and orthogonal projection

Two vectors ${\vec {a}}$ and ${\vec {b}}$ are orthogonal if and only if their scalar product is zero, i.e.

$\vec a \perp \vec b \iff \vec a \cdot \vec b = 0.$

The orthogonal projection of ${\vec {b}}$ onto the direction given ${\vec {a}}$ vector is the vector $\vec b_{\vec a} = k \vec a$ with

$k = \frac{\vec b \cdot \vec a}{\vec a \cdot \vec a}= \frac{\vec b \cdot \vec a}{|\vec a|^2},$

${\vec {b}}_{\vec {a}}={\frac {{\vec {b}}\cdot {\vec {a}}}{|{\vec {a}}|^{2}}}\,{\vec {a}}=\left({\vec {b}}\cdot {\frac {\vec {a}}{|{\vec {a}}|}}\right)\,{\frac {\vec {a}}{|{\vec {a}}|}}.$

The projection is the vector whose endpoint is the plumb line from the endpoint of ${\vec {b}}$ to the straight line through the origin determined by ${\vec {a}}$ The vector $\vec b - \vec b_{\vec a}$ is perpendicular to $\vec a.$

If ${\vec {a}}$ a unit vector (i.e. if $|\vec a| = 1$ ), the formula simplifies to

${\vec {b}}_{\vec {a}}=({\vec {b}}\cdot {\vec {a}})\,{\vec {a}}.$

Reference to the cross product

Another way to multiplicatively link two vectors ${\vec {a}}$ and ${\vec {b}}$ in three-dimensional space is the outer product or cross product $\vec a \times \vec b.$ Unlike the scalar product, the result of the cross product is not a scalar, but again a vector. This vector is perpendicular to the plane ${\vec {b}}$ spanned by the two vectors ${\vec {a}}$ and and its length corresponds to the area of the parallelogram spanned by them.

The following calculation rules apply to the connection of the cross product and the scalar product:

$({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}={\vec {a}}\cdot ({\vec {b}}\times {\vec {c}})$
$({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}=-({\vec {b}}\times {\vec {a}})\cdot {\vec {c}}$
$({\vec {a}}\times {\vec {b}})\cdot {\vec {a}}=({\vec {a}}\times {\vec {b}})\cdot {\vec {b}}=0$
$( \vec a \times \vec b ) \cdot ( \vec a \times \vec b ) = ( \vec a \cdot \vec a ) ( \vec b \cdot \vec b ) - ( \vec a \cdot \vec b )^2$

The combination of cross product and scalar product of the first two rules is also called spar product; it gives the oriented volume of the parallelepiped $\vec a, \vec b, \vec c$ spanned by the three vectors .

Applications

In geometry

The scalar product makes it possible to prove complicated theorems involving angles in a simple way.

Assertion: (cosine theorem)

$c^2=a^2+b^2-2\,a\,b\,\cos\gamma.$

Proof: Using the vectors drawn in, it follows ${\vec {c}}=-{\vec {b}}+{\vec {a}}.$ (The direction of $\vec c$ is irrelevant.) Squaring the magnitude yields

$|{\vec {c}}|^{2}={\vec {c}}\cdot {\vec {c}}=({\vec {a}}-{\vec {b}})\cdot ({\vec {a}}-{\vec {b}})={\vec {a}}\cdot {\vec {a}}-2\,{\vec {a}}\cdot {\vec {b}}+{\vec {b}}\cdot {\vec {b}}=|{\vec {a}}|^{2}+|{\vec {b}}|^{2}-2\,{\vec {a}}\cdot {\vec {b}}$

and thus

$c^{2}=a^{2}+b^{2}-2\,a\,b\,\cos \gamma .$

In physics

In physics, many quantities, such as the work are defined by scalar products:

$W=\vec F \cdot \vec s = |\vec F| |\vec s| \cos \varphi = F_s \cdot s = F \cdot h$

with the vectorial quantities force ${\vec {F}}$ and displacement ${\vec {s}}$ . Here φ {\displaystyle $\varphi$ denotes the angle between the direction of the force and the direction of the path. F_s denotes the component of the force in the direction of the path, the component of the path in the direction of the force.

Example: A wagon of weight is transported over an inclined plane from to The work of lifting calculated as

$\begin{align} W &= \vec F \cdot \vec s = F \cdot h = F \cdot s \cdot \cos \varphi \\ &= 5\,\mathrm N \cdot 3\,\mathrm m \cdot \cos 63^\circ = 6{,}81 \,\mathrm J. \end{align}$

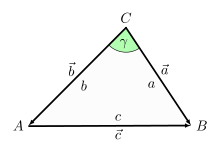
Cosine theorem with vectors

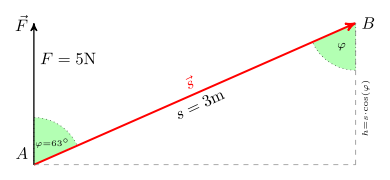
Example inclined plane

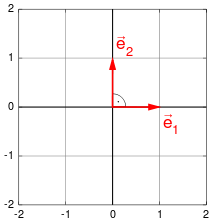
Canonical unit vectors in the Euclidean plane

Orthogonal projection $\vec b_{\vec a}$ the vector ${\vec {b}}$ onto the ${\vec {a}}$ direction determined by

Questions and Answers

Q: What is the dot product in mathematics?

A: The dot product is an operation that takes two vectors as input and returns a scalar number as output.

Q: What does the dot product depend on?

A: The dot product depends on the length of both vectors and on the angle between them.

Q: Why is the name of the dot product derived from the centered dot "·"?

A: The name is derived from the centered dot "·" that is often used to designate this operation.

Q: What is the alternative name for the dot product?

A: The alternative name is scalar product, which emphasizes the scalar (rather than vector) nature of the result.

Q: What is the contrast between the dot product and the cross product in three-dimensional space?

A: The dot product produces a scalar number as result, while the cross product produces a vector as result.

Q: What is the dot product used for in mathematics?

A: The dot product can be used to determine if two vectors are perpendicular (have an angle of 90 degrees), and to project one vector onto another.

Q: Can the dot product be used in higher-dimensional spaces?

A: Yes, the dot product can be extended to higher-dimensional spaces by generalizing the definition.