Doppler effect

This article is about the Doppler effect. For the influence of kinetic energy in nuclear reactions, see Doppler broadening; for the music project of the same name, see Doppler effect (band).

The Doppler effect (rarely Doppler-Fizeau effect) is the temporal compression or stretching of a signal with changes in the distance between transmitter and receiver during the duration of the signal. The cause is the change in propagation time. This purely kinematic effect occurs with all signals that propagate at a certain speed, usually the speed of light or sound. If the signal propagates in a medium, its state of motion must be taken into account.

With periodic signals, the observed frequency increases or decreases. This applies to pitches as well as modulation frequencies, e.g. the change of tones of a Martin horn ("tatü...taataa"). For low velocities relative to the propagation velocity, this ratio also gives the relative frequency change Δ . ${\frac {\Delta f}{f}}$ For reflected signals, as in radar Doppler and ultrasound Doppler, the Doppler shift Δ \Delta f}{f}} also doubles with the propagation time $\Delta f$ .

Change of the wavelength with movement of the sound source

Change of wavelength due to Doppler effect

Details of the acoustic Doppler effect

When explaining the acoustic Doppler effect, it is necessary to distinguish whether the sound source, the observer, or both are moving relative to the medium (the stationary air).

Observer at rest, signal source moving

As an example, assume that the ambulance's siren emits sound waves with a frequency of 1000 Hz. This means that exactly 1/1000 seconds after the first wave crest a second wave crest follows. The waves propagate with the speed of sound $c\approx 340\,{\mathrm {m/s}}$ at 20 °C.

As long as the ambulance is stationary, the wavelength λ $\lambda _{{\mathrm {S}}}$ of the sound, that is, the distance between the crests of the waves:

$\lambda _{\mathrm {S} }=340\,\mathrm {\frac {m}{s}} \cdot {\frac {1}{1000}}\,\mathrm {s} =0{,}34\,\mathrm {m} \,.$

For an observer on the road, these crests do arrive somewhat delayed depending on the distance. However, the time between two crests does not change. The fundamental frequency $f_{\mathrm {S} }$ of the perceived sound is the same for any distance between the observer and the ambulance.

The situation changes when the ambulance moves towards the observer with speed . As the car continues to move in the time between the two crests, the distance between them shortens slightly. It shortens by the distance the cart travels in the time of 1/1000 of a second:

$\lambda _{\mathrm {B} }=\lambda _{\mathrm {S} }-{\frac {v_{\mathrm {S} }}{f_{\mathrm {S} }}}\,.$

The indices ${\mathrm {S}}$ and $\mathrm {B}$ refer to the sender and observer of the wave, respectively. Since both wave crests travel at the same speed of sound to the observer, the shortened distance between them is preserved, and the second wave crest arrives not 1/1000 second after the first, but a little earlier. Referring to the above example, the wavelength shortens at a speed of $36\,{\mathrm {{\frac {km}{h}}}}=10\,{\mathrm {{\frac {m}{s}}}}$ :

} $\lambda _{\mathrm {B} }=0{,}34\,\mathrm {m} -{\frac {10\mathrm {\frac {m}{s}} }{1000\mathrm {\frac {1}{s}} }}=0{,}33\,\mathrm {m} \,.$

As a result, the frequency (i.e. the pitch) of the siren appears higher to the observer ( $f_{{\mathrm {B}}}>f_{{\mathrm {S}}}$ ):

} $f_{\mathrm {B} }={\frac {c}{\lambda _{\mathrm {B} }}}={\frac {340\,\mathrm {\frac {m}{s}} }{0{,}33\,\mathrm {m} }}\approx 1030{,}3\,\mathrm {Hz} \,.$

Quantitatively, the frequency change is obtained simply by substituting the relation λ $\lambda \cdot f=c$ into the above formula for λ $\lambda _{{\mathrm {B}}}$ . For the frequency perceived by the observer $f_{{\mathrm {B}}}$ thus results:

} $f_{\mathrm {B} }={\frac {f_{\mathrm {S} }}{1-{\frac {v}{c}}}}\,.$		(1)

Where $f_{\mathrm {S} }$ the frequency of the sound source, is the propagation velocity of the sound, and is the velocity of the sound source (i.e., the ambulance).

When the ambulance has passed the observer, the reverse is true: the distance between the crests (wavelength) increases and the observer hears a lower tone. Mathematically, the above formula applies in the same way, you just have to insert a negative velocity for . Related to the example:

} $\lambda _{\mathrm {B} }=0{,}34\,\mathrm {m} -{\frac {-10\,\mathrm {\frac {m}{s}} }{1000\mathrm {\frac {1}{s}} }}=0{,}35\,\mathrm {m} \qquad {\text{und somit}}\qquad f_{\mathrm {B} }={\frac {c}{\lambda _{\mathrm {B} }}}={\frac {340\,\mathrm {\frac {m}{s}} }{0{,}35\,\mathrm {m} }}\approx 971{,}4\,\mathrm {Hz} \,.$

The described movements of the signal source directly towards or directly away from the observer are special cases. If the signal source moves arbitrarily in space with velocity ${\vec {v}}$ then the Doppler shift for a receiver at rest can be given by

$f_{\mathrm {B} }={\frac {f_{S}}{1-{\frac {{\vec {v}}\cdot {\vec {e}}_{\mathrm {SB} }}{c}}}}$

${\vec {e}}_{{\mathrm {SB}}}$ here is the time-dependent unit vector representing the direction from the signal source ${\mathrm {S}}$ to the observer $\mathrm {B}$ .

Observer moving, signal source at rest

Even with the sound source ${\mathrm {S}}$ and moving observer $\mathrm {B}$ a Doppler effect occurs, but here the cause is different: When the car is at rest, the distance between the wave crests does not change either, so the wavelength remains the same. However, the wave crests seem to arrive at the observer faster one after the other, when the observer moves towards the ambulance:

${\begin{aligned}\lambda _{\mathrm {B} }&=\lambda _{\mathrm {S} }\,,\\(c+v)\,T_{\mathrm {B} }&=c\,T_{\mathrm {S} }\end{aligned}}$

respectively

} $f_{\mathrm {B} }=f_{\mathrm {S} }\left(1+{\frac {v}{c}}\right)\,.$		(2)

Again, the case of a receding observer results from inserting a negative velocity.

For an arbitrary motion of the observer $\mathrm {B}$ with velocity vector ${\vec {v}}$ when the transmitter rest, the Doppler effect ${\mathrm {S}}$ the Doppler effect becomes

$f_{\mathrm {B} }=f_{\mathrm {S} }\left(1-{\frac {{\vec {v}}\cdot {\vec {e}}_{\mathrm {SB} }}{c}}\right)$

Where ${\vec {e}}_{{\mathrm {SB}}}$ again the unit vector describing the direction from the signal source ${\mathrm {S}}$ to the observer $\mathrm {B}$ , which in the general case, just like the velocity vector ${\vec {v}}$ , can be time dependent.

As can be seen, equations (1) and (2) are not identical (only in the limiting case $v\ll c$ they approach each other). This becomes obvious in the extreme case: if the observer moves towards the signal source at the speed of sound, the wave crests reach him twice as fast, and he hears a sound of twice the frequency. If, on the other hand, the signal source is moving at the speed of sound, the distance between the wave crests is practically zero, they overlap and there is extreme compression of the air (see sound barrier breakthrough). Since all wave crests arrive at the observer at the same time, this would theoretically be an infinite frequency according to the formula above - in practice, one does not hear a sound of a specific frequency, but the sonic boom.

Observer and signal source moved

By combining equations (1) and (2), one can derive an equation describing the frequency $f_{{\mathrm {B}}}$ when the transmitter and receiver are in motion.

Transmitter and receiver move towards each other:

$f_{\mathrm {B} }=f_{\mathrm {S} }\cdot {\frac {1+{\frac {v_{\mathrm {B} }}{c}}}{1-{\frac {v_{\mathrm {S} }}{c}}}}=f_{\mathrm {S} }\cdot {\frac {c+v_{\mathrm {B} }}{c-v_{\mathrm {S} }}}\,.$

Transmitter and receiver move away from each other:

$f_{\mathrm {B} }=f_{\mathrm {S} }\cdot {\frac {1-{\frac {v_{\mathrm {B} }}{c}}}{1+{\frac {v_{\mathrm {S} }}{c}}}}=f_{\mathrm {S} }\cdot {\frac {c-v_{\mathrm {B} }}{c+v_{\mathrm {S} }}}\,.$

Where $v_{\mathrm {B} }$ the velocity of the observer and $v_{\mathrm {S} }$ is the velocity of the sender of the sound waves relative to the medium.

Frequency shift in case of scattering by a moving object

Also from the above equations, the perceived frequency can be derived when the wave from a stationary transmitter is scattered by an ${\mathrm {S}}$ object ${\vec {v}}$ moving with velocity is $\mathrm{O}$ scattered and perceived by an observer also at rest:. $\mathrm {B}$ perceived:

$f_{\mathrm {B} }=f_{\mathrm {S} }{\frac {1-{\frac {{\vec {v}}\cdot {{\vec {e}}_{\mathrm {SO} }}}{c}}}{1-{\frac {{\vec {v}}\cdot {\vec {e}}_{\mathrm {OB} }}{c}}}}\,.$

${\vec {e}}_{\mathrm {SO} }$ and ${\vec {e}}_{\mathrm {OB} }$ are respectively the unit vectors from the stationary transmitter to the moving object and from the moving object to the stationary observer.

This equation is often used in acoustic or optical metrology to measure motion, e.g. laser Doppler anemometry. Especially in optics, for $\left|{\vec {v}}\right|\ll c$ the angular dependence of the scattered frequency can be given by

$f_{\mathrm {B} }\approx f_{\mathrm {S} }\left(1+{\frac {\vec {v}}{c}}\cdot ({\vec {e}}_{\mathrm {OB} }-{\vec {e}}_{\mathrm {SO} })\right)$

from illumination direction ${\vec {e}}_{\mathrm {SO} }$ and observation direction ${\vec {e}}_{\mathrm {OB} }$ can be determined to a very good approximation.

General Doppler law for sound sources

In general, the frequency difference can be written as:

$f_{\mathrm {B} }=f_{\mathrm {S} }\left({\frac {c\pm v_{\mathrm {B} }}{c\mp v_{\mathrm {S} }}}\right)\,.$

Where $v_{\mathrm {B} }$ the velocity of the observer and $v_{\mathrm {S} }$ that of the sound source, each relative to the medium (e.g., air). The upper operation sign applies in each case to approach (movement in the direction of the transmitter or receiver). I.e. both velocities are measured positively in the direction of the observer or transmitter. With $v_{\mathrm {B} }=0$ or , $v_{\mathrm {S} }=0$ the above special cases arise. For $v_{\mathrm {S} }=-v_{\mathrm {B} }$ the effect disappears (so there is no pitch change). This occurs when the transmitter and receiver are moving in the same direction at the same speed relative to the medium; usually in such cases the medium itself is moving while the transmitter and receiver are at rest (wind). This is why there is no Doppler effect regardless of the strength of the wind.

The formulas were derived under the assumption that the source and observer are moving directly towards each other. In real cases, for example, the ambulance passes the observer at a certain minimum distance. Therefore, the distance between the source and the observer does not change uniformly, and that is why - especially immediately before and after passing - a continuous transition of the pitch from higher to lower can be heard.

Wave fronts of a point source moving relative to the medium demonstrate the dependence of the wavelength on the propagation direction

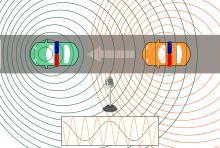
Doppler effect using the example of two moving police cars and a stationary microphone

Doppler effect without medium

Electromagnetic waves also propagate in a vacuum, i.e. without a medium. If the sender of the waves moves relative to the receiver, a shift in frequency also occurs in this case. This relativistic Doppler effect is due to the fact that the waves propagate with finite speed, namely the speed of light. It can be understood as a geometric effect of space-time.

Longitudinal Doppler effect

In a vacuum (optical Doppler effect), the observed frequency change depends only on the relative velocity of the source and observer; whether the source, the observer, or both are moving has no effect on the magnitude of the frequency change.

Due to the principle of relativity, every observer may consider himself to be at rest. However, when calculating the Doppler effect, in addition to the above considerations, he must then also take into account the time dilation of the source moving relative to the observer. Thus one obtains for the relativistic Doppler effect:

$f_{\mathrm {B} }={\frac {f_{\mathrm {S} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}{1-{\frac {v}{c}}}}=f_{\mathrm {S} }{\sqrt {\frac {c+v}{c-v}}}$

v > 0 when the distance between the source and the observer is reduced.

Transverse Doppler effect

If an object is moving transversely (which means "across", see the next two sections) to the observer at a certain point in time, the change in distance at this point in time can be neglected; accordingly, one would not expect a Doppler effect here. However, relativity theory states that every object is subject to time dilation due to its motion, due to which the frequency is also reduced. This effect is called the transverse Doppler effect. The formula for this is

$f_{\mathrm {B} }={\frac {f_{\mathrm {S} }}{\gamma }}=f_{\mathrm {S} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\approx f_{\mathrm {S} }\left(1-{\frac {v^{2}}{2c^{2}}}\right)\,,$

where denotes here the vacuum light velocity and the velocity of the signal source.

However, the transverse Doppler effect can be neglected at non-relativistic velocities (i.e. velocities far below the speed of light).

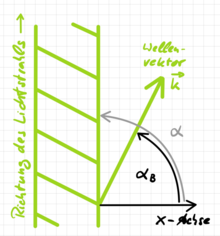
Doppler effect at any angle

The Doppler effect can be specified quite generally as a function of the angle of observation. The frequency change for any observation angle α is given $\alpha _{\mathrm {B} }$ by

$f_{\mathrm {B} }=f_{\mathrm {S} }{\frac {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}{1-{\frac {v}{c}}\cos {\alpha _{\mathrm {B} }}}}\,.$

If for the angle α $\alpha _{\mathrm {B} }$ is set to 0° (source moving directly towards receiver), 90° (source moving sideways) or 180° (source moving directly away from receiver), then the above equations for longitudinal and transverse Doppler effect are obtained. It can also be seen that the angle at which the Doppler effect disappears depends on the relative velocity, unlike the Doppler effect for sound, where it is always 90°.

The angle of observation α $\alpha _{\mathrm {B} }$

Due to the finite transit time between the source and receiver, the angle of observation α $\alpha _{\mathrm {B} }$ from the actual angle α $\alpha$ between the direction of motion of the source and the source-receiver axis. The angle of observation α $\alpha _{\mathrm {B} }$ is the angle between the direction of motion of the source and the "local" wave vector at the observer's location at a given time. The local wavefront is perpendicular to this wave vector. The local wave vector, or the local wave front, are the optically relevant quantities, e.g. in the astronomical observation of a passing star.

Particularly illustrative is the difference between the angle of observation α $\alpha _{\mathrm {B} }$ and the actual angle α $\alpha$ , considering a laser pointer moving with velocity along the axis and emitting light at an angle α $\alpha$ with respect to the direction of motion, i.e., the axis. To do this, we compare the and components of the speed of light in the observer's rest frame with the $c_{x}'$ and $c_{y}'$ components of the speed of light relative to the moving laser. The component of the speed of light relative to the laser pointer does not change, i.e., $c_{y}'=c_{y}$ . For the component, on the other hand, we need to subtract $c_{x}'=c_{x}-v$ . Thus, we obtain the following relation between the angle α $\alpha$ , which the laser beam includes with the axis and the angle α $\alpha _{\mathrm {B} }$ formed by the wave vector with the axis:

$\tan \alpha ={\frac {\sin \alpha _{\mathrm {B} }}{\cos \alpha _{\mathrm {B} }-{\frac {v}{c}}}}$ .

Where we still used the following relations: $\sin \alpha _{\mathrm {B} }=c_{y}/c$ and $\cos \alpha _{\mathrm {B} }=c_{x}/c$ . In particular, we obtain a light beam radiating perpendicular to the direction of motion, i.e., α $\alpha =90^{\circ }$ , if $\cos \alpha _{\mathrm {B} }=v/c$ . Now the special thing is: This perpendicular light beam has an additional lateral drift motion of velocity . Its wave fronts are still aligned perpendicular to the wave vector, but the wave vector no longer points perpendicularly upwards, i.e. in the direction of the light beam, but encloses $\arcsin(v/c)$ the angle with the axis.

By the way: The transverse Doppler effect and especially this laterally drifting light beam is the key to a vivid and self-consistent description of special relativity. According to the above formula, for the case $\cos \alpha _{\mathrm {B} }=v/c$ , the frequency of this light beam is $f_{B}=\gamma f_{S}$ . Thus, if one sets a laser pointer in motion, then the electromagnetic field in the laser resonator must be given an amount of energy proportional to

$(\gamma -1)f_{S}\approx {\frac {1}{2}}{\frac {v^{2}}{c^{2}}}f_{S}$

are supplied to the laser. Knowing now that is $f_{S}$ proportional to the rest energy $E_{0}$ of the electromagnetic field of the laser resonator, the formula E follows $1/2mv^{2}$ directly when comparing with the kinetic energy $E_{0}=mc^{2}$ , where can be taken as the mass of energy stored in the resonator.

Doppler effect and astronomical redshift

Even though the observed effects of the Doppler effect and astronomical redshift are identical (reduction of the observed frequency of the electromagnetic radiation of a star or galaxy), the two should not be confused, since they have entirely different causes.

The relativistic Doppler effect is the main cause of the frequency change only if the transmitter and receiver move through space-time as described above and their distance is so small that the expansion of the space between them is relatively small. From a certain distance on, the part caused by the expansion of space-time itself predominates by far, so that the part of the Doppler effect discussed here can be completely neglected.

Play media file Lateral drifting light beam: The light beam here is not generated by a moving laser pointer that shines vertically upwards, but by a moving 45° mirror.

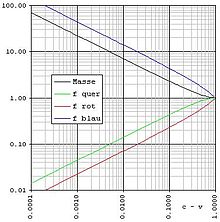
Relativistic Doppler effect and velocity

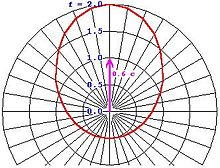
Relativistic Doppler effect and direction

Comparison between the angles α $\alpha _{\mathrm {B} }$ and α $\alpha$ in the case of a laterally drifting light beam, or in the case of the transverse Doppler effect. $\alpha _{\mathrm {B} }$ is the angle at which a passing object is observed. $\alpha$ is the angle with respect to the line connecting the source and the observer.

Questions and Answers

Q: What is the Doppler effect?

A: The Doppler effect is a change in frequency and wavelength of a wave caused by the change in distance between the thing creating the wave and whatever is measuring, seeing or hearing the wave.

Q: What causes the Doppler effect?

A: The change in distance between the thing creating the wave and whatever is measuring, seeing or hearing the wave causes the Doppler effect.

Q: What is another word for "causer" in the Doppler effect?

A: Another word for "causer" in the Doppler effect is "sender" or "source".

Q: What is another word for "change in distance" in the Doppler effect?

A: Another word for "change in distance" in the Doppler effect is "speed" or "relative velocity".

Q: Can all types of waves be affected by the Doppler effect?

A: Yes, all the waves that can be sent out or reflected by an object can be affected by the Doppler effect.

Q: What is reflection in the context of the Doppler effect?

A: In the context of the Doppler effect, reflection refers to the change in direction of a wave.

Q: Can the sender of a wave experience the Doppler effect?

A: No, the sender of a wave does not experience the Doppler effect.