Diffie–Hellman key exchange

This is the sighted version that was marked on 11 January 2021. There is 1 pending change that needs to be sighted.

The Diffie-Hellman key exchange or Diffie-Hellman-Merkle key exchange or key agreement (also abbreviated to DHM key exchange or DHM protocol) is a protocol for key agreement. It enables two communication partners to agree on a common secret key in the form of a number via a public, interceptable line, which only they know and which a potential eavesdropper cannot calculate. The agreed key can then be used for a symmetric cryptosystem (for example, Data Encryption Standard or Advanced Encryption Standard). Different variants of the Diffie-Hellman-Merkle method are used today for key distribution in the communication and security protocols of the Internet, for example in the areas of electronic commerce. This principle thus has important practical significance.

The method was developed by Whitfield Diffie and Martin Hellman and published in 1976 under the name ax1x2. It is the first of the so-called asymmetric crypto methods (also public key crypto methods) to be published. Important preliminary work was done by Ralph Merkle with the Merkle puzzle named after him. As only became known in 1997, employees of the British Government Communications Headquarters (GCHQ) were the first to develop asymmetric cryptosystems in the early 1970s. However, GCHQ never applied for a patent because of secrecy and because of the questionable usefulness for the British from the perspective of the early 1970s.

The DHM key exchange is one of the crypto systems based on the discrete logarithm (DL methods for short). These are based on the fact that the discrete exponential function is a one-way function in certain cyclic groups. Thus, in the prime residue class group, the discrete exponential function $b^{x}\ {\bmod {\ }}p$ , prime, can be calculated efficiently even for large exponents, but its inverse, the discrete logarithm, cannot. To date, no "fast" algorithm exists for calculating the exponent , given base module and the desired result.

With this method, the researchers also coined a new concept of security in cryptography, which is based on the fact that no efficient algorithm exists for cryptanalysis: A communication protocol is secure if its cryptanalysis means so much time and work that it cannot be carried out in practice. The problem of calculating the secret key from the two messages of the communication partners is called the Diffie-Hellman problem.

However, the DHM key exchange is no longer secure if an attacker interposes himself between the two communication partners and can modify messages. Protocols such as the Station-to-Station protocol (STS) close this gap by additionally using digital signatures and message authentication codes.

The implementation using elliptic curves is known as Elliptic Curve Diffie-Hellman (ECDH). Here, the operations used in the original method (multiplication and exponentiation) on the finite body are replaced by point addition and scalar multiplication on elliptic curves. The -fold addition of a point to itself (i.e. multiplication by the scalar ) is denoted by and corresponds to an exponentiation $b^{n}$ in the original method. The principle was proposed independently by Victor S. Miller and Neal Koblitz in the mid-1980s.

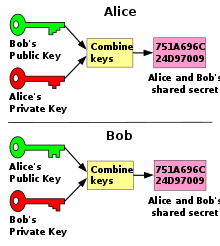
Agreement of a shared secret key over an interceptable line with the Diffie-Hellman-Merkle key exchange

History and significance

Public cryptology

The Diffie-Hellman-Merkle key exchange is the first of the so-called asymmetric crypto methods (also public key crypto methods) to be published. It solves the key exchange problem by making it possible to agree on secret keys via non-secret, i.e. public, channels.

The first step towards the development of asymmetric procedures was taken by Ralph Merkle in 1974 with Merkle's puzzle, which was named after him, but was not published until 1978. Under the influence of this work, Whitfield Diffie and Martin Hellman developed the Diffie-Hellman key exchange in 1976. They published the research paper under the title "New Directions in Cryptography". The procedure provided a huge push in cryptography, a science that had not been practised publicly for very long at that time. Originally, the researchers called the procedure ax1x2. In 2002, Martin Hellman suggested calling the procedure Diffie-Hellman-Merkle key exchange, "if names are already associated with it", in recognition of Ralph Merkle's part in the development of asymmetric procedures.

The significance of this development is also compared with the Copernican turn: "The development of asymmetric encryption has a comparable significance for cryptography as the Copernican turn had for astronomy and, along with the digitisation of information and the internet as a communication platform, represents a foundation of the third millennium".

Whitfield Diffie and Martin Hellman also coined a new concept of security in cryptography with the method, which is based on the fact that no efficient algorithm exists for cryptanalysis: A communication protocol is secure if its cryptanalysis means so much time and work that it cannot be carried out in practice. The security of the Diffie-Hellman-Merkle key exchange is decisively based on the fact that the discrete exponential function is a one-way function in certain cyclic groups, especially in the prime residue class group. This means that in this group, exponentiation can be calculated efficiently, but for its inverse, the discrete logarithm, no efficient algorithm is known to date.

The Diffie-Hellman-Merkle method is now only one of many methods that use the discrete exponential function (with discrete logarithm as the inverse) as a one-way function. In this context, one also speaks of crypto systems based on the discrete logarithm or simply DL methods. For example, it is closely related to the Elgamal encryption method, which was developed by the cryptologist Taher Elgamal in 1985. In principle, this is nothing more than a DHM key exchange followed by the sending of a message encrypted with the agreed key.

In the fundamental "New Directions" work, the researchers also introduced the concept of a digital signature: a sender calculates a value called a digital signature for a digital message (i.e. any data) using a secret signature key (the private key). This value enables anyone to check the non-repudiable authorship and integrity of the message with the help of the public verification key. Thus, as a further development of the DHM key exchange, a diverse family of digital signatures based on the discrete logarithm emerged. Among the best known are the Elgamal signature method and the Digital Signature Algorithm.

In addition to the one-way function, Whitfield Diffie and Martin Hellman also developed the concept of the trapdoor. This is a "hidden shortcut" using additional information to make the otherwise difficult reversal simple. On the basis of trapdoor functions, asymmetric procedures can be developed in which the transmission of a secret key is no longer necessary. In this way, they also did important preliminary work for the development of the RSA cryptosystem. Ronald L. Rivest, Adi Shamir and Leonard Adleman actually tried to prove that such trapdoor functions cannot exist. However, during the proof tests, they actually came across such a one-way function with a trapdoor. In 1977, this led to the development of the most famous public key algorithm, the RSA cryptosystem, named after the initials of its inventors.

Different variants of the DHM procedure are used today for key distribution in the communication and security protocols of the Internet, such as IPsec (Internet Protocol Security), IPv6 (Internet Protocol Version 6) and TLS (Transport Layer Security). These are used to secure the transmission of data packets of the IP protocol layer or data of the application layer, for example in the areas of electronic commerce. This principle of key distribution thus has an important practical significance. The key automatically calculated here is then used as the key for a fast symmetrical procedure such as Data EncryptionStandard (DES) or Advanced Encryption Standard (AES).

The concept of public-key cryptography and some specific methods were protected until 1997 by U.S. Patents 4,200,770 (Hellman, Diffie, Merkle, 1980) and 4,218,582 (Hellman, Merkle, 1980), owned by Stanford University. For the development of public-key cryptography and digital signatures, Whitfield Diffie and Martin Hellman were awarded the Turing Award in 2015, which is considered the highest award in computer science, comparable to the Nobel Prize or the Fields Medal.

Secret cryptology

As only became known in 1997, the British Government Communications Headquarters (GCHQ) had already given the order in the 1960s to find another way to avoid the high costs of the then usual key distribution. James H. Ellis formulated the concept of "non-secret encryption". From this, Clifford Cocks developed a procedure which he described in an internal document as early as 1973 and which is very similar to the RSA procedure. Thus, from today's perspective, it must be stated that Clifford Cocks was actually the first to develop an asymmetric crypto method. This achievement is not generally acknowledged to him, as his work was by definition classified and therefore not published at the time. It was not until 1997 that the internal document was published on the Communications Electronics Security Group website.

In this context, it also became known that Malcolm Williamson, another GCHQ employee, discovered the Diffie-Hellman key exchange method as early as 1975. What is interesting here is that the discovery of the two procedures - RSA and DHM - in public and secret cryptology took place in reverse order.

Clifford Cocks

Ralph Merkle

Whitfield Diffie

Martin Hellman

Key exchange problem

Encryption methods in which two participants use the same secret key are called symmetric methods. Let Alice and Bob be the sender and receiver of messages over an eavesdropping channel, and let Eve be an eavesdropper who tries to read messages. With a good encryption method, it is impossible for Eve to decrypt a message without knowing the key, even if she knows the encryption method. Thus Kerckhoffs' principle states that the security of a procedure must be based solely on the secrecy of a key (and not on the secrecy of the encryption algorithm). A message that is encrypted is called plaintext, the encrypted text ciphertext.

An important prerequisite for secure symmetric communication is therefore that the key has already been exchanged between Alice and Bob via a secure channel, for example by a trusted courier or during a direct meeting. The following problem now arises in the key exchange problem: Alice wants to communicate with Bob, who is overseas, for example, using a symmetric encryption method. The two are connected via an unsecure line and have not exchanged a key. How do Alice and Bob agree on a common secret key over an insecure channel?

A manual key exchange has the disadvantage that it becomes quite confusing when a larger group of users wants to communicate among themselves in encrypted form. With communication partners, $n\cdot (n-1)/2$ keys are required if everyone wants to communicate with everyone else. With 50 communication partners, a total of 1,225 keys would therefore be required.

The Diffie-Hellman method provides an elegant solution to these problems: it allows Alice and Bob to agree on a secret key over the public, unsecured line without Eve finding out the key.

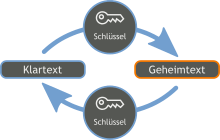
Encryption and decryption with the same key (symmetrical procedure)

Functionality

Illustration of the basic idea using mixed colours

First of all, the basic idea of the Diffie-Hellman-Merkle key exchange is to be illustrated by means of "colour mixing" as shown in the illustration on the left. In reality, the colours would be numbers and the mixing of colours would correspond to the discrete exponential function.

The mixing of colours is understood here as a one-way function: It is "easy" to mix two or more different colours. However, the reversal, the breaking down of a colour mixture into its original colour components, is very time-consuming, i.e. not efficiently feasible.

Alice and Bob first publicly agree on a common colour (yellow in the example). In addition, each of the two communication partners chooses a secret colour for themselves (Alice orange and Bob turquoise). Bob and Alice now each mix the common colour with their secret colour. In the example, this results in beige for Alice and grey-blue for Bob. Alice and Bob now exchange these colour mixtures over the wire. A potential eavesdropper Eve cannot efficiently deduce the secret colours of Alice and Bob from the public information (yellow, beige, grey-blue).

In a final step, Alice and Bob mix the colour mixture of their counterpart with their own secret colour. This in turn creates a new colour (ochre brown in the example) that is the same for both communication partners (yellow + orange + turquoise = yellow + turquoise + orange = ochre brown). Thus Alice and Bob have a common secret colour. It is impossible for Eve to find this out because she does not know Alice's and Bob's secret colour ingredients.

Mathematical functioning

The two communication partners Alice and Bob want to communicate in encrypted form via an insecure medium, such as a cable or radio connection. For this purpose, a symmetrical cryptosystem is to be used, for which, however, both first need a common secret key. The DHM communication protocol ensures that they can calculate a secret key without third parties (Eve) being able to learn it. They can then use the key calculated in this way in the future to communicate in encrypted form with a symmetric cryptosystem.

Alice and Bob first publicly agree on a large prime number and a natural number which is smaller than Agreeing publicly means that everyone is allowed to know these two numbers (so also potential eavesdroppers like Eve). Ideally, a producer of the cyclic group $\mathbb {Z} _{p}$ but the procedure also works if takes another value smaller than In practice, it is usually the case that and predefined and used by many users.
Alice and Bob each generate a random number to be kept secret (private key) and from the set $\{1,\ldots ,p-1\}$ . and are not transmitted, thus remain unknown to potential eavesdroppers, but also to the respective communication partner. Only Alice knows the number and only Bob knows the number .
Alice calculates the public key with her secret number $A=g^{a}\ {\bmod {\ }}p$ and sends to Bob. Bob uses his secret number to calculate the public key $B=g^{b}\ {\bmod {\ }}p$ and sends to Alice.
Alice receives from Bob and calculates with her private key the number $K_{1}=B^{a}\ {\bmod {\ }}p$ . Bob also calculates the number K with the obtained A and his private key $K_{2}=A^{b}\ {\bmod {\ }}p$ . The two have calculated the same number $K_{1}=K_{2}$ This is therefore the common key looking for.

Only Alice and Bob know . Eve cannot calculate from the intercepted communication. To do so, she would have to solve the discrete logarithm, which, according to current knowledge, cannot be done efficiently if the numbers are large enough. Alice and Bob can therefore safely use for symmetric encryption.

That both communication partners calculate the same value for is shown by the following two residual class equations:

$K_{1}=B^{a}\ {\bmod {\ }}p=(g^{b}\ {\bmod {\ }}p)^{a}\ {\bmod {\ }}p=(g^{b})^{a}\ {\bmod {\ }}p=g^{ba}\ {\bmod {\ }}p$ .

$K_{2}=A^{b}\ {\bmod {\ }}p=(g^{a}\ {\bmod {\ }}p)^{b}\ {\bmod {\ }}p=(g^{a})^{b}\ {\bmod {\ }}p=g^{ab}\ {\bmod {\ }}p$ .

Since multiplication is commutative, the following also applies

$g^{ba}\ {\bmod {\ }}p=g^{ab}\ {\bmod {\ }}p$

and thus

$K_{1}=K_{2}$ .

So Alice and Bob get exactly the same number after their respective calculations, namely the secret key $K=K_{1}=K_{2}$ .

Example:

The following example is for illustrative purposes and therefore uses very small numbers. In the actual application, however, numbers with at least several hundred digits are used.

Alice and Bob agree on the two public keys and ( is a generator of the group $\mathbb {Z} _{13}^{*}$ , see section "Group Theory").
Alice chooses the random number as the secret key and Bob .
Now Alice calculates $A=g^{a}\ {\bmod {\ }}p=2^{5}\ {\bmod {\ }}13=6$ and sends to Bob. Bob calculates $B=g^{b}\ {\bmod {\ }}p=2^{8}\ {\bmod {\ }}13=9$ and sends to Alice.
Alice calculates $K_{1}=B^{a}\ {\bmod {\ }}p=9^{5}\ {\bmod {\ }}13=3$ . Bob calculates $K_{2}=A^{b}\ {\bmod {\ }}p=6^{8}\ {\bmod {\ }}13=3$ .
Both get the same result $K=K_{1}=K_{2}=3$ .

Eve, the eavesdropper, can listen in on the numbers 13, 2, 6 and 9, but the actual shared secret of Alice and Bob K=3 remains hidden from her. K=3 can be used as a key for the following communication.

With the help of the intercepted messages, Eve can at least come up with the following equations:

$6=2^{a}\ {\bmod {\ }}13$

$9=2^{b}\ {\bmod {\ }}13$

From this, for example, she can $b=8$ determine the two secret numbers a=5 and by trial and error. The agreed key of Alice and Bob can now be determined with

$K=g^{ab}\ {\bmod {\ }}p$

calculate.

However, if the prime chosen large enough and a generator of the group $\mathbb {Z} _{p}^{*}$ , it is too much work for Eve to p-1 try all numbers between and which are possible results of the modular power } $g^{a}\ {\bmod {\ }}p$ .

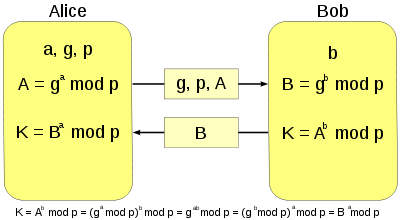
Principle of Diffie-Hellman-Merkle key exchangea : private key of Aliceb: private key of Bobp: publicly known prime numberg : publicly known natural number smaller than pA : public key of AliceB: public key of BobK: secret session key for Alice and Bob

Security

Diffie-Hellman problem

Computational Diffie Hellman Problem (CDH)

Suppose that the eavesdropper Eve learns on the unsecure line the numbers , , and but not the discrete logarithms of and of to the base . Knowing and it would be an easy task for them to determine the key $K=g^{ab}\ {\bmod {\ }}p$ However, finding the numbers and is very difficult when the numbers and are very large, for example numbers with several hundred digits in the decimal system. This problem results in the computational Diffie-Hellman problem:

Given an element of a group and the values $A=g^{a}$ and $B=g^{b}$ what is the value of $K=g^{{ab}}$ with unknown ?

Since this problem can only be solved in certain groups with enormous computational effort, an attacker cannot calculate the generated key from the two messages transmitted during the Diffie-Hellman-Merkle key exchange.

The Diffie-Hellman problem is closely related to the discrete logarithm problem. Calculating discrete logarithms is the only known method to break the DHM procedure. Unless this can be solved in a reasonable amount of time, it is impossible for an attacker to determine the secret key. However, it has not been proven that this is indeed the only method, i.e. whether someone who could solve the Diffie-Hellman problem could also compute discrete logarithms efficiently. Ueli Maurer has shown that both problems are equivalent, at least under certain conditions.

Decisional Diffie Hellman Problem (DDH)

If it is to be impossible for an attacker to obtain any information about the transported key from the publicly available information, the Decisional-Diffie-Hellman problem (DDH) must be unassailable. This problem can be described as follows:

An attacker receives three numbers: $A=g^{a}\ {\bmod {\ }}p$ , $B=g^{b}\ {\bmod {\ }}p$ and $C=g^{c}\ {\bmod {\ }}p$ . Here, either , and randomly and equally distributed in $\{0,...,p-2\}$ or $c=ab\ {\bmod {\ }}p$ set In the second case, is called (A,B,C) Diffie-Hellman triple. The attacker must decide whether such a triple exists or not. If he cannot, it is impossible for him to draw conclusions from g^a and g^b $g^{ab}$

So the problem is, given $g^{a}\ {\bmod {\ }}p$ , $g^{b}\ {\bmod {\ }}p$ and $g^{c}\ {\bmod {\ }}p$ decide whether $g^c = g^{ab}$ .

Anyone who can solve the computational Diffie-Hellman problem is obviously also capable of solving the decisional Diffie-Hellman problem. This is not clear for the reverse case.

Given a choice of as a primitive root, the Decisional-Diffie-Hellman problem can be attacked. This is due to the following theorem:

Let be a prime number, let be a primitive root modulo and let $a,b\in \{0,...,p-2\}$ . Then $g^{ab}$ is a quadratic residue modulo if g^a or g^b is a quadratic residue modulo .

The theorem follows that a power of is a quadratic residue modulo exactly when the exponent is even.

An attacker can therefore check whether the criterion from this theorem is fulfilled. Although he cannot always decide whether a Diffie-Hellman triple is present, he answers 75% correctly. His advantage over pure guessing is therefore 50 %.

Choice of public numbers

DHM prime number p

The safety of the method is based not least on the length of the chosen numbers. The prime number must be chosen so that discrete logarithms modulo calculated (efficiently enough) with currently known methods. The larger the prime number used, the more secure the method, but also the more complex. The Federal Office for Information Security recommends a key length of at least 3000 bits for (as of 2017).

The DHM prime must also be chosen so that algorithms for calculating the discrete logarithm do not have an easy time. For example, it must be avoided that has p-1 only small prime factors. Otherwise, namely, the Pohlig-Hellman algorithm can be applied, which does not depend on the group order, but on the largest factor of the group order. Furthermore, should be as unsuitable as possible for the number sieve. This is the case if there is an irreducible polynomial of degree 5 that has very small coefficients and a zero ${\bmod {\ }}p$

"Generator" g

The number should be chosen in such a way that all numbers between and p-1 can be considered as the result of the modular power $g^{a}\ {\bmod {\ }}p$ Only then is it too costly to try all numbers (if, in addition, the prime number been chosen large enough). This property is fulfilled by the number if it is a primitive root of the modulus , i.e. a producer of the group $\mathbb {Z} _{p}^{*}$ . For example, if Alice and Bob g=1 choose the procedure still works, but the key is in any case because is exactly the generator of the subgroup of $\mathbb {Z} _{p}^{*}$ with one element. The procedure is similarly uncertain if Alice and Bob choose a generator of a different small subgroup for The procedure is safer with a generator of a large subgroup, but it is best to choose a generator of the whole group right away. Since half of all numbers smaller than are such generators, there is enough choice.

As shown in the section "Prime residue class group and primitive root", it is relatively easy to find a primitive root by choosing the DHM prime as $p=2\times q+1$ with a prime However, as shown in the previous section, the Decisional-Diffie-Hellman problem can be attacked by choosing as a primitive root.

"If instead one chooses such that the residue class of modulo has prime order with a sufficiently large prime then DDH is considered difficult by today's standards."

- Johannes Buchmann, 2016

Use of fixed groups and prime numbers

Since generating safe primes is computationally expensive, many implementations use a fixed prime . Some network protocols, such as Internet Key Exchange, provide a list of possible groups and their prime number.

The use of fixed groups and primes can be exploited by an attacker to perform much of the computation to break the discrete logarithm in advance and to attack multiple targets simultaneously. The number sieve algorithm consists of four steps, the first three of which require only the prime If is known, an attacker can thus precompute the bulk and reuse the results for each key exchange based on This allows, for example, the Logjam attack in TLS, after a week of precomputation, to break a 512-bit DHM key exchange in about 70 seconds.

A team of researchers estimates that with pre-computation of the 10 most common 1024-bit primes, an attacker can decrypt network traffic from 66% of VPNs, 26% of SSH servers, 16% of SMTP servers and 24% of HTTPS websites on the internet. The researchers estimate that the computational effort to break 1024-bit Diffie-Hellman can be done by a state attacker such as the National Security Agency.

Man-in-the-middle attack

→ Main article: Man-in-the-middle attack

The Diffie-Hellman-Merkle key exchange is no longer secure if the attacker can modify data packets in a man-in-the-middle attack. In the Alice and Bob model, such an attacker who can actively intervene is called Mallory (from malicious). In a man-in-the-middle attack, Mallory intercepts the messages sent by Alice and Bob and sends his own message instead.

$Z=g^{z}\mod p$

which he calculates from an arbitrary number and the publicly known numbers and

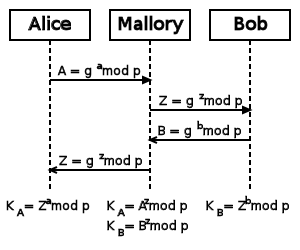
Man-in-the-Middle-Angriff

After the key exchange, the two communication partners Alice and Bob have different keys $K_{A}$ and $K_{B}$ . In principle, a DHM key exchange was carried out twice: once between Alice and attacker Mallory and once between Mallory and Bob. Here Mallory gains knowledge of the two keys $K_{A}$ and $K_{B}$ .

$K_{A}=Z^{a}{\bmod {p}}=(g^{z})^{a}{\bmod {p}}=(g^{a})^{z}{\bmod {p}}=A^{z}{\bmod {p}}$

$K_{B}=Z^{b}{\bmod {p}}=(g^{z})^{b}{\bmod {p}}=(g^{b})^{z}{\bmod {p}}=B^{z}{\bmod {p}}$

Since Alice and Bob assume that they are communicating with each other, Mallory can listen to the following symmetrically encrypted communication. He continues to redirect this communication via himself. Mallory decrypts data from Alice with $K_{A}$ and encrypts it again with $K_{B}$ before sending it on to Bob. In the process, Mallory can both read and change the message content without being noticed. He uses the same procedure for the opposite direction.

To exclude such a man-in-the-middle attack, the exchanged messages must be authenticated. This requires an information advantage, which is achieved via an authenticated channel.

Side channel attacks

A side-channel attack refers to a cryptanalytic method that exploits the physical implementation of a cryptosystem in a device (e.g. a smart card, a security token or a hardware security module) or in software. In this case, it is not the cryptographic procedure itself that is attacked, but only a specific implementation. The principle is based on observing a cryptographic device during the execution of cryptological algorithms and finding correlations between the observed data and the key used.

Time attack

In 1995, Paul Kocher published a novel method with which he succeeded in breaking implementations of Diffie-Hellman, RSA and DSA: the timing attack.

The target of the time attack is the discrete exponential function. When a crypto implementation computes $g^{a}\ {\bmod {\ }}p$ for any larger numbers and , then this is almost always done with the square-and-multiply algorithm. In this, an action is set for each bit of If the currently processed bit has the value , then this action is a multiplication, otherwise a squaring. Since the computing times for the multiplications take longer than for the squares, Eve can draw conclusions about the number of ones in from time measurements. If he varies the number at some point the information is sufficient to calculate With just a few thousand time measurements, corresponding implementations can be broken with 1024-bit keys.

In order to prevent such time attacks, however, only delays must be built into the encryption or decryption process during implementation. With the procedure known as blinding, for example, a random number is included at one point in the procedure, which is then subtracted again at another point. Another possibility is to design the process in such a way that it always takes the same amount of time, regardless of the input value.

Power attack

In 1998, Paul Kocher, Joshua Jaffe and Benjamin Jun first introduced the concept of current attack. In power attacks, not only the processing time is measured, but also the power consumption with an oscilloscope. Smartcards are particularly vulnerable to power attacks because they rely on an external power supply. An attacker measures the encryption and decryption processes and tries to assign certain points of the power consumption curve to individual components of the process. Here, too, the square-and-multiply algorithm is a suitable target, as multiplications and squaring can often be easily distinguished by the power consumption. Current attacks are somewhat more complex to carry out than time attacks, but are considered more effective.

As a countermeasure against power attacks, the manufacturer of crypto modules can disguise the power consumption by incorporating dummy operations into an encryption or decryption process. Another possibility is to create an artificial power noise that overlays the actual power consumption.

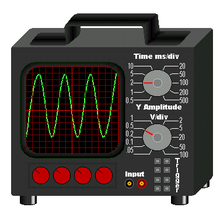
In a current attack, an oscilloscope measures the current consumption of a process.

Elliptic Curve Diffie-Hellman (ECDH)

Cryptosystems based on elliptic curves (ECC procedures for short, from Elliptic Curve Cryptography) are not cryptographic procedures in their own right, but known DL procedures that are implemented in a special way. Every procedure based on the discrete logarithm in finite bodies can be transferred in a simple way to elliptic curves and thus transformed into an elliptic curve cryptosystem. Here, the operations used in the original method (multiplication and exponentiation) on the finite body are replaced by point addition and scalar multiplication on elliptic curves. The -fold addition of a point to itself (i.e. multiplication by the scalar ) is denoted by and corresponds to an exponentiation $x^{n}$ in the original method. The principle was proposed independently by Victor S. Miller and Neal Koblitz in the mid-1980s.

Body

A body is a set provided with two inner two-digit links " " and " $\cdot$ , usually called "addition" and "multiplication". A body is an abelian group with respect to addition and multiplication without zero and the distributive laws apply. The best-known body is the set of real numbers $\mathbb {R}$ on which addition and multiplication are defined in the usual way.

For a prime number the set of numbers between $0$ and p-1 forms a group with both modulo addition and modulo multiplication without zero. The residue classes of integers modulo , written $\mathbb {F} _{p}$ or $\operatorname {GF} (p)$ thus form a finite body (also Galois field). Furthermore, for every prime number and every natural number (except for isomorphism) there is exactly one body with $p^{n}$ elements, which can be compared with $\mathbb {F} _{p^{n}}$ or $\operatorname {GF} (p^{n})$ . In Elliptic Curve Cryptography, the two special cases n=1 and p=2 of particular importance, i.e. $\operatorname {GF} (p)$ and $\operatorname {GF} (2^{n})$ . These are the best for implementing ECC procedures.

Elliptic curves

An elliptic curve (EC) is a set of points (x,y) with values from a body that satisfy a cubic equation of the following form:

$y^{2}=x^{3}+ax+b$ . (Short Weierstrass equation)

The (real) coefficients and must $4a^{3}+27b^{2}\neq 0$ satisfy the condition to exclude singularities.

An elliptic curve is a smooth algebraic curve of order 3 in the projective plane. Elliptic curves are usually represented as curves in the affine plane, but they also have an additional point at infinity, which is referred to here as ${\mathcal O}$ (pronounced "O"), but is not to be confused with the zero point of the coordinate system. Above the body $K = \R$ of the real numbers, the points form a curve in the real plane.

An important property of elliptical curves is the following: If a straight line intersects such a curve, then there are exactly three intersection points. The following cases occur:

For a straight line parallel to the axis, one of the three intersections is ${\mathcal O}$ .
For a straight line that touches the curve, the point of contact is counted as a double intersection.
For all other straight lines the intersections are obvious.

By this property, elliptic curves can be used to define a group $\operatorname {E} (K)$ defined:

Let be the set of points of an elliptic curve, unified with the point ${\mathcal O}$ at infinity. One defines the group operation, usually called point addition, as follows:

To calculate the sum of two points and , draw a straight line through and (if draw the tangent to EC through )
Find the third intersection point this line with the curve EC. (If the line is parallel to the axis, this intersection is ${\mathcal O}$ .)
sum is the point of EC formed by mirroring on the axis. The reflection of ${\mathcal O}$ is again ${\mathcal O}$ .

The neutral element of the group is ${\mathcal O}$ . It is valid $P+{\mathcal {O}}={\mathcal {O}}+P=P$ for all points of the elliptic curve. The inverse of a point is obtained by applying to it a straight line parallel to the axis. If this straight line is a tangent, then the point itself is its inverse element.

The point P+P is denoted by , accordingly one defines $kP=P+\ldots +P$ as -fold addition of the point . If is not the ${\mathcal O}$ point, then any point on the curve E can be reached in this way (i.e., for every point on the curve there exists a natural number with $Q=kP$ ) if one knows the correct generators of the group. (See also section Group Operation in the article "Elliptic Curve").

The task of finding P,Q this value from given points called the elliptic curve discrete logarithm problem (ECDLP for short). It is assumed that the ECDLP (with a suitable choice of curves) is difficult, i.e. cannot be solved efficiently. Thus, elliptic curves lend themselves to realising asymmetric cryptosystems on them.

Very illustrative is the construction for $K = \R$ since the points can be expressed in the real plane. However, this construction can be transferred to any body. In cryptography, elliptic curves of the form $\operatorname {E} (\operatorname {GF} (p))$ and $\operatorname {E} (\operatorname {GF} (2^{n}))$ significant.

Example:

Let the elliptic curve be

$E:y^{2}=x^{3}+x+1$

over the body $K=\operatorname {GF} (5)$ given.

So it is a=1 and b=1 and it is $4a^{3}+27b^{2}=31\ {\bmod {\ }}5=1\neq 0$ . The set of all (x,y) with $x,y\in \operatorname {GF} (5)$ and $y^{2}=x^{3}+x+1$ is thus together with ${\mathcal O}$ an elliptic curve over $\operatorname {GF} (5)$ .

This results in the following points:

	$x^{3}+x+1\ {\bmod {\ }}5$		Points
$0$		and $4(=-1\ {\bmod {\ }}5)$	,
		- –	- –
		and	,
		and	, $(3,4)$
		and	$(4,2)$ ,
${\mathcal O}$	- –	${\mathcal O}$	${\mathcal O}$

Diffie-Hellman based on elliptic curves

In cryptosystems based on elliptic curves, instead of arithmetic operations in $\operatorname {GF} (p)$ operations in $\operatorname {E} (\operatorname {GF} (p))$ or $\operatorname {E} (\operatorname {GF} (2^{n}))$ used. Again, efficient algorithms exist in these bodies for calculating the power function, but not for calculating the logarithm.

Instead of a modulus, Alice and Bob now have to agree on a particular elliptic curve, i.e. a body $\operatorname {GF} (p)$ (or $\operatorname {GF} (2^{n})$ ) and a group $\operatorname {E} (\operatorname {GF} (p))$ (or $\operatorname {E} (\operatorname {GF} (2^{n}))$ ). All parameters that are in the exponent are (as before) natural numbers, while the base of a power is an element of $\operatorname {E} (\operatorname {GF} (p))$ is.

An exponentiation over $\operatorname {E} (\operatorname {GF} (p))$ is more complex than an exponentiation over $\operatorname {GF} (p)$ since it is composed of several arithmetic operations in $\operatorname {GF} (p)$ . For this, the calculation of the logarithm in $\operatorname {E} (\operatorname {GF} (p))$ considerably "more difficult". The central advantage of using $\operatorname {E} (\operatorname {GF} (p))$ is therefore that Alice and Bob can use a smaller power group with the same security. This results in shorter key lengths, shorter signatures and shorter computation times.

The complexity of the logarithm increases linearly in increases linearly $\operatorname {E} (\operatorname {GF} (p))$ with , but in $\operatorname {GF} (p)$ on the other hand "only" logarithmically. A key length of 1,024 bits based on the discrete logarithm can, for example, be shortened to 200 bits by using elliptic curves without any loss of security. The saving in computing time is usually stated to be a factor of 10.

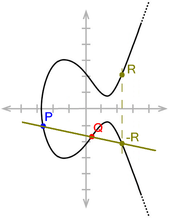
Addition of points P and Q on an elliptic curve

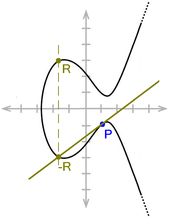
Doubling of a point P on an elliptic curve

Ephemeral Diffie-Hellman

In the context of the encryption protocol Transport Layer Security (TLS), Ephemeral Diffie-Hellman refers to the use of Diffie-Hellman with new parameters for each new TLS session. With static Diffie-Hellman, the same parameters derived from a public-key certificate are reused for each TLS session. In both cases, the same algorithm is used and only the parameters differ.

Using Ephemeral Diffie-Hellman to negotiate a symmetric session key provides forward secrecy, as opposed to encrypted transmission of a session key using a public key encryption scheme, for example RSA.