Differential of a function
In calculus, a differential refers to the linear part of the increase of a variable or a function and describes an infinitely small section on the axis of a coordinate system. Historically, the term was at the core of the development of infinitesimal calculus in the 17th and 18th centuries. From the 19th century onwards, analysis was mathematically correctly rebuilt by Augustin Louis Cauchy and Karl Weierstrass on the basis of the limit value concept, and the concept of the differential lost its significance for elementary differential and integral calculus.
If there is a functional dependence 




where 




Differentials are used today in different applications with different meanings and also with different mathematical rigour. The differentials appearing in standard notations such as 

A rigorous definition is provided by the theory of differential forms used in differential geometry, where differentials are interpreted as exact 1-forms. A different kind of approach is provided by non-standard analysis, which takes up the historical concept of the infinitesimal number again and specifies it in the sense of modern mathematics.
Classification
In his "Lectures on Differential and Integral Calculus", first published in 1924, Richard Courant writes that the idea of the differential as an infinitely small quantity has no meaning and that it is therefore useless to define the derivative as the quotient of two such quantities, but that one could nevertheless try to define the expression 








In more modern terminology, the differential in can be thought of 







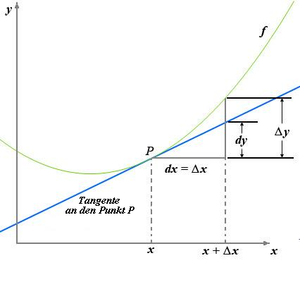
The differential as linearised increment
If 






For example, if 





For functions whose slope is not constant, the situation is more complicated. If 



If one now considers for Δ 

then the following follows for the increase of the function value

In this representation, Δ 






Definition
Let 




the differential of 





For a fixed 



For example, for the identical function 




Higher order differentials
If 



the 










The meaning of this definition is explained by Courant as follows. If thought to be fixed,













For a fixed 




Calculation rules
Regardless of the definition used, the following calculation rules apply to differentials. In the following, denotes 





and the derivation rules. The following calculation rules for differentials of functions 





Constant and constant factor
and
Addition and subtraction
; and
Multiplication
also called product rule:
Division
Chain rule
- If
depends on
and depends on
, so
and
, then holds

Examples
- For
and
or
. It follows

- For
and
and
, thus

Extension and variants
Instead of 
- By ∂
(introduced by Condorcet, Legendre and then Jacobi one sees it in old French cursive, or as a variant of the cursive Cyrillic d) is meant a partial differential.
- With δ
(the Greek small delta) denotes a virtual displacement, the variation of a location vector. It is therefore related to the partial differential according to the individual spatial dimensions of the location vector.
- δ
denotes an inexact differential.
Total differential
→ Main article: Total differential
The total differential or complete differential of a differentiable function 


This is again interpretable as the linear part of the increment. A change of the argument by Δ 


where the first summand is the scalar product of the two 



Virtual shift
→ Main article: Virtual work
A virtual displacement δ 



The 



The holonomic constraints are thus explicitly eliminated by selecting and correspondingly reducing the generalised coordinates.
Stochastic Analysis
In stochastic analysis, the differential notation is often used, for example, to notate stochastic differential equations; it is then always to be understood as a shorthand notation for a corresponding equation of Itō-integrals. For example, if 

given equation for a process 

Today's approach: differentials as 1-forms
→ Main article: Pfaff's form and differential form
The definition of the differential given above 










The total differential or the outer derivative 








Using the gradient and the standard scalar product, the total differential of can be given by
represent.
For 


Differentials in the integral calculus
Clear explanation
To calculate the area of a region bounded by the graph of a function 






the total area, i.e. the sum
where here 
![[a, b]](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
![[a, b]](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)


![[a, b]](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
The total interval ![[a,b]](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
![[a,b]](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
Formal explanation
→ Main article: "Integration of differential forms" in the article Differential form
Let 

is a 1-form which can be integrated according to the rules of integration of differential forms. The result of the integration over an interval ![\left[a,b\right]](https://www.alegsaonline.com/image/f30926fb280a9fdf66fd931e14d4363cb824feaa.svg)

Historical
Gottfried Wilhelm Leibniz uses the integral sign for the first time in a manuscript in 1675 in the treatise Analysis tetragonistica, he does not write 





In the modern version of this approach to integral calculus according to Bernhard Riemann, the "integral" is a limit value of the area contents of finitely many rectangles of finite width for ever finer subdivisions of the " 
Therefore, the first symbol in the integral is a stylised S for "sum". "Utile erit scribi 






Blaise Pascal's reflections on the quadrant arc: Quarts de Cercle
When Leibniz was a young man in Paris in 1673, he received a decisive stimulus from a reflection by Pascal in his 1659 paper Traité des sinus des quarts de cercle (Treatise on the sine of the quarter circle). He says he saw a light in it that the author had not noticed. It is the following (written in modern terminology, see illustration):
To reduce the static moment
of the quadrant arc with respect to the x-axis, Pascal deduces from the similarity of the triangles with the sides
and
that their aspect ratio is the same
and thus
so that
applies. Leibniz now noticed - and this was the "light" he saw - that this procedure is not limited to the circle, but applies in general to any (smooth) curve, provided that the radius of the circle a is replaced by the length of the normal of the curve (the reciprocal curvature, the radius of the circle of curvature). The infinitesimal triangle
is the characteristic triangle (It is also found in Isaac Barrow for tangent determination.) It is remarkable that the later Leibnizian symbolism of the differential calculus (dx, dy, ds) corresponds precisely to the point of view of this "improved indivisibility conception".
Similarity
All triangles from a section Δ 





Nova methodus 1684
A new method of maxima, minima, and tangents, which does not interfere with fractional or irrational quantities, and a peculiar method of calculating them. (Leibniz (G. G. L.), Acta eruditorum 1684)
Leibniz explains his method very briefly on four pages. He chooses any independent fixed differential (here dx, see fig. r. above) and gives the calculation rules, as below, for the differentials, describing how to form them.
Then he gives the chain rule:
"Thus it comes about that for every equation presented one can write down its differential equation. This is done by simply inserting for each member (i.e. each constituent which contributes to the production of the equation by mere addition or subtraction) the differential of the member, but for another quantity (which is not itself a member but contributes to the formation of a member) applying its differential in order to form the differential of the member itself, not without further ado, but according to the algorithm prescribed above."
This is unusual from today's point of view, because he considers independent and dependent differentials equally and individually, and not the differential quotient of dependent and independent quantity as finally required. The other way round, when he gives a solution, the formation of the differential quotient is possible. He deals with the whole range of rational functions. There follows a formal complicated example, a dioptric one of light refraction (minimum), an easily solvable geometric one, with entangled distance relations, and one dealing with the logarithm.
Further connections are considered scientifically historically with him from the context of earlier and later works on the subject, some of which are only available in manuscript or in letters and not published. In Nova methodus 1684, for example, it is not stated that for the independent dx dx = const. and ddx=0. In further contributions he treats the subject up to "roots" and quadratures of infinite series.
Leibniz describes the relationship between infinitesimal and known differential (= size):
"It is also clear that our method masters the transcendental lines which cannot be traced back to the algebraic calculus or are of no definite degree, and this applies quite generally, without any special, not always applicable, presuppositions. It is only necessary to state once and for all that to find a tangent is as much as to draw a straight line connecting two points of the curve at an infinitely small distance, or an extended side of the infinite-cornered polygon, which for us is synonymous with the curve. But that infinitely small distance can always be expressed by some known differential, such as dv, or by a relation to it, i.e. by a certain known tangent."
For the transcendent line, the cycloid is used as proof.
As an appendix, in 1684 he explains the solution of a problem posed by Florimond de Beaune to Descartes, which he did not solve. The problem involves finding a function (w, of the line WW in Plate XII) whose tangent (WC) always intersects the x axis in such a way that the intercept between the point of intersection of the tangent with the x axis and its distance from the associated abscissa x, there he chooses dx always equals b, is constant, he calls it a here. He compares this proportionality with the arithmetic series and the geometric series and obtains the logarithms as abscissa and the numeri as ordinate. "Thus the ordinates w" (increase in value) "become proportional to the dw" (increase in slope)", their increments or differences, ..." He gives the logarithm function as the solution: "... if the w are the numeri, the x are the logarithms.": w=a/b dw, or w dx = a dw. This satisfies
or
Cauchy's differential term
In the 1980s, a debate took place in Germany about the extent to which Cauchy's foundation of analysis is logically sound. With the help of a historical reading of Cauchy, Detlef Laugwitz tries to make the concept of infinitely small quantities fruitful for his Ω 
Cauchy's differentials are finite and constant 


The relation to 



Their geometric relationship is defined as
determined. Cauchy can transfer this ratio of infinitely small quantities, or more precisely the limit of geometric difference ratios of dependent numerical quantities, a quotient, to finite quantities.
Differentials are finite number quantities whose geometric ratios are strictly equal to the limits of the geometric ratios formed by the infinitely small increments of the presented independent variables or the variables of the functions. Cauchy considers it important to regard differentials as finite number quantities.
The calculator makes use of the infinitesimals as mediators, which must lead him to the knowledge of the relationship that exists between the finite number magnitudes; and in Cauchy's opinion, the infinitesimals must never be admitted in the final equations, where their presence would remain meaningless, purposeless and useless. Moreover, if one were to consider the differentials as constantly very small number magnitudes, then one would thereby give up the advantage which consists in the fact that among the differentials of several variables one can take the one as a unit. For in order to form a clear conception of any number magnitude, it is important to relate it to the unit of its genus. It is therefore important to select a unit from among the differentials.
In particular, the difficulty of defining higher differentials falls away for Cauchy. For Cauchy sets 


…

First content page
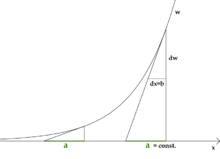
Graphical illustration of the Beaune problem
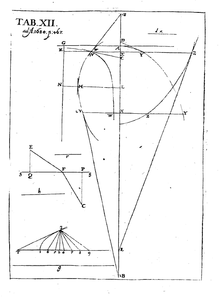
Plate XII
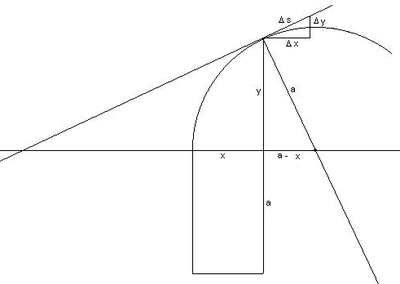
The characteristic triangle
See also
- Differential equation
Search within the encyclopedia