Determinant

The title of this article is ambiguous. For other meanings, see Determinant (disambiguation).

In linear algebra, the determinant is a number (a scalar) that is assigned to a square matrix and can be calculated from its entries. It indicates how the volume changes in the linear mapping described by the matrix and is a useful tool in solving systems of linear equations. More generally, one can assign a determinant to each linear self-mapping (endomorphism). Common notations for the determinant of a square matrix are $\det(A)$ $\det A$ or |A| .

For example, the determinant of a $2\times 2$ matrix can be

$A={\begin{pmatrix}a&c\\b&d\end{pmatrix}}$

with the formula

$\det A={\begin{vmatrix}a&c\\b&d\end{vmatrix}}=ad-bc$

be calculated.

With the help of determinants, for example, one can determine whether a linear system of equations is uniquely solvable and can explicitly state the solution with the help of Cramer's rule. The system of equations is uniquely solvable exactly when the determinant of the coefficient matrix is not equal to zero. Accordingly, a square matrix with entries from a body is exactly invertible if its determinant is not equal to zero.

If one writes vectors in $\mathbb {R} ^{n}$ as columns of a square matrix, the determinant of this matrix can be formed. If, in this determination, the vectors form a basis, the sign of the determinant can be used to define the orientation of Euclidean spaces. The absolute value of this determinant also corresponds to the volume of the n-parallelotope (also called spat) spanned by these vectors.

If the linear mapping $f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{n}$ represented by the matrix and $S\subseteq \mathbb {R} ^{n}$ is any measurable subset, then it follows that the volume of f(S) $\left|\det A\right|\cdot \operatorname {Volumen} (S)$ given by

If the linear mapping $f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}$ represented by the $m\times n$ matrix and $S\subseteq \mathbb{R} ^{n}$ is any measurable subset, then in general the -dimensional volume of f(S) $\textstyle {\sqrt {\det(A^{T}A)}}\cdot \operatorname {Volumen} (S)$ given by

The concept of determinant is of interest for $(n\times n)$ matrices with For n=1 it degenerates to triviality $\det a=a$ : Thus a linear system of equations for the case n=1 of an equation ax=b . Solvability criterion and strategy for this equation are known: If $a\neq 0$ set $x:=a^{-1}b$ .

The 2x2 determinant is equal to the oriented area of the parallelogram spanned by its column vectors

Definition

There are several ways to define the determinant (see below). The most common is the following recursive definition.

Development of the determinant according to a column or row:

For n=2:

${\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}}=a_{11}a_{22}-a_{21}a_{12}$

For n=3: Development according to the 1st column

$|A|={\begin{vmatrix}{\color {red}a_{11}}&a_{12}&a_{13}\\{\color {blue}a_{21}}&a_{22}&a_{23}\\{\color {red}a_{31}}&a_{32}&a_{33}\end{vmatrix}}={\color {red}a_{11}}\,{\begin{vmatrix}\Box &\Box &\Box \\\Box &a_{22}&a_{23}\\\Box &a_{32}&a_{33}\end{vmatrix}}-{\color {blue}a_{21}}\,{\begin{vmatrix}\Box &a_{12}&a_{13}\\\Box &\Box &\Box \\\Box &a_{32}&a_{33}\end{vmatrix}}+{\color {red}a_{31}}\,{\begin{vmatrix}\Box &a_{12}&a_{13}\\\Box &a_{22}&a_{23}\\\Box &\Box &\Box \end{vmatrix}}$

$={\color {red}a_{11}}\,{\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}}-{\color {blue}a_{21}}\,{\begin{vmatrix}a_{12}&a_{13}\\a_{32}&a_{33}\end{vmatrix}}+{\color {red}a_{31}}\,{\begin{vmatrix}a_{12}&a_{13}\\a_{22}&a_{23}\end{vmatrix}}$

Correspondingly for n=4,....

Laplace's development theorem (see below) says:

You may develop a determinant according to any column or row, as long as you keep to the chessboard sign pattern:

${\begin{vmatrix}{\color {red}+}&{\color {blue}-}&{\color {red}+}&\cdots \\{\color {blue}-}&{\color {red}+}&{\color {blue}-}&\cdots \\{\color {red}+}&{\color {blue}-}&{\color {red}+}&\cdots \\\cdots &\cdots &\cdots &\cdots \end{vmatrix}}$

Formally, it can be written like this:

$\det A=\sum _{i=1}^{n}(-1)^{i+j}\cdot a_{ij}\cdot \det A_{ij}$ (development according to the -th column)

$\det A=\sum _{j=1}^{n}(-1)^{i+j}\cdot a_{ij}\cdot \det A_{ij}$ (development after the -th line),

where $A_{ij}$ is the $(n-1)\times (n-1)$ submatrix of obtained by deleting the i}th row and j}th column

Example:

${\begin{vmatrix}0&1&2\\3&2&1\\1&1&0\end{vmatrix}}=0\cdot {\begin{vmatrix}2&1\\1&0\end{vmatrix}}-3\cdot {\begin{vmatrix}1&2\\1&0\end{vmatrix}}+1\cdot {\begin{vmatrix}1&2\\2&1\end{vmatrix}}$

$=0\cdot (2\cdot 0-1\cdot 1)-3\cdot (1\cdot 0-1\cdot 2)+1\cdot (1\cdot 1-2\cdot 2)=0+6-3=3$

Properties (summary, see below)

$\det E=1$ for unit matrix
$\det \left(A^{\textsf {T}}\right)=\det(A)$ where is $A^{\textsf {T}}$ the transposed matrix of
$\det \left(A^{-1}\right)={\frac {1}{\det(A)}}.$
For square matrices and same size, the determinant multiplication theorem applies:

$\det(AB)=\det(A)\det(B).$

$\det(cA)=c^{n}\det(A)$ for an $n\times n$ matrix and a number .
For a triangular matrix $\ \det(A)=a_{11}a_{22}\cdots a_{nn}\ .$
If a row or column consists of zeros, the determinant is 0.
If two columns (rows) are equal, the determinant is 0.
If you swap two columns (rows), a determinant changes its sign.
If $v_{1},...,v_{n}$ the column vectors (row vectors) of a matrix and is a number, then the following applies:

a1) $\det(v_{1}+{\color {red}w},v_{2},...v_{n})=\det(v_{1},v_{2},...,v_{n})+\det({\color {red}w},v_{2},...,v_{n})$

a2) $\det({\color {red}c}v_{1},v_{2},...v_{n})={\color {red}c}\det(v_{1},v_{2},...v_{n})$ ,

correspondingly for the other column vectors (row vectors).

b) $\det(v_{1},...v_{n})$ is the (oriented) volume (area in case n=2) of the polytope (parallelogram) $v_{1},...v_{n}$ spanned by the vectors

Addition of a multiple of one column (row) to another column (row) does not change a determinant. One can therefore transform a determinant into a triangular determinant with a weakened Gauss algorithm and use property 6. Note property 9. and 10.a2).
Only for $3\times 3$ -determinants Sarrus' rule applies:

Example, application of rules 11, 10, 8:

${\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}}={\begin{vmatrix}1&2&3\\3&3&3\\6&6&6\end{vmatrix}}=2{\begin{vmatrix}1&2&3\\3&3&3\\3&3&3\end{vmatrix}}=0$

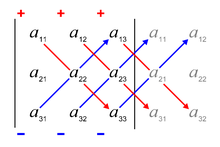
Rule of Sarrus

Axiomatic description

A mapping $\det \colon K^{n\times n}\to K$ from the space of square matrices into the underlying body maps each matrix to its determinant if it satisfies the following three properties (axioms according to Karl Weierstrass), where a square matrix is written column-wise as $A=(v_{1},\dotsc ,v_{n})$ :

It is multilinear, i.e. linear in each column:

For all $v_{1},\ldots ,v_{n},w\in K^{n}$ holds:

${\begin{aligned}&\det(v_{1},\ldots ,v_{i-1},v_{i}+w,v_{i+1},\ldots ,v_{n})\\&=\det(v_{1},\ldots ,v_{i-1},v_{i},v_{i+1},\ldots ,v_{n})+\det(v_{1},\ldots ,v_{i-1},w,v_{i+1},\ldots ,v_{n})\end{aligned}}$

For all $v_{1},\ldots ,v_{n}\in K^{n}$ and all $r\in K$ holds:

$\det(v_{1},\ldots ,v_{i-1},r\cdot v_{i},v_{i+1},\ldots ,v_{n})=r\cdot \det(v_{1},\ldots ,v_{i-1},v_{i},v_{i+1},\ldots ,v_{n})$

It is alternating, i.e. if two columns contain the same argument, the determinant is equal to 0:

For all $v_{1},\ldots ,v_{n}\in K^{n}$ and all $i,j\in \{1,\ldots ,n\},i\neq j$ holds:

$\det(v_{1},\ldots ,v_{i-1},v_{i},v_{i+1},\ldots ,v_{j-1},v_{i},v_{j+1}\ldots ,v_{n})=0$

It follows that the sign changes when two columns are swapped:

For all $v_{1},\ldots ,v_{n}\in K^{n}$ and all $i,j\in \{1,\ldots ,n\},i\neq j$ holds:

$\det(v_{1},\ldots ,v_{i},\ldots ,v_{j},\ldots ,v_{n})=-\det(v_{1},\ldots ,v_{j},\ldots ,v_{i},\ldots ,v_{n})$

This inference is often used to define alternating. In general, however, it is not equivalent to the above. If alternating is defined in the second way, there is no unique determinant form if the body over which the vector space is formed has an element different from 0 with x=-x (characteristic 2).

It is normalised, i.e. the unit matrix has the determinant 1:

$\det E_{n}=1$

It can be proved (and Karl Weierstrass did so in 1864 or even earlier) that there is one and only one such normalised alternating multilinear form on the algebra of $n\times n$ matrices over the underlying body - namely, this determinant function $\det$ (Weierstrass determinant labelling). The already mentioned geometric interpretation (volume property and orientation) also follows from this.

Leibniz formula

For an $n\times n$ matrix, the determinant was $A=(a_{{ij}})\in K^{{n\times n}}$ defined by Gottfried Wilhelm Leibniz by the formula for the determinant of a matrix known today as the Leibniz formula:

$\det A = \sum_{\sigma \in S_n} \left(\operatorname{sgn}(\sigma) \prod_{i=1}^n a_{i, \sigma(i)}\right)$

The sum is calculated over all permutations σ $\sigma$ the symmetric group $S_{n}$ degree n. $\operatorname {sgn} (\sigma )$ denotes the signum of the permutation σ $\sigma$ (+1 if σ $\sigma$ an even permutation and -1 if it is odd) and σ $\sigma (i)$ is the function value of the permutation σ $\sigma$ at location .

This formula contains summands and therefore becomes more unwieldy the larger is. However, it is well suited for proving statements about determinants. For example, with its help the continuity of the determinant function can be seen.

An alternative notation of the Leibniz formula uses the Levi-Civita symbol and Einstein's summation convention:

$\det A=\varepsilon _{i_{1}i_{2}\dots i_{n}}a_{1i_{1}}a_{2i_{2}}\dots a_{ni_{n}}$

Determinant of an endomorphism

Since similar matrices have the same determinant, the definition of the determinant of square matrices can be transferred to the linear self-mappings (endomorphisms) represented by these matrices:

The determinant $\det f$ of a linear mapping $f\colon V\to V$ a vector space in itself is the determinant $\det A$ a representation matrix of with respect to a basis of . It is independent of the choice of basis.

Here can be any finite-dimensional vector space over any body . More generally, one can also consider a commutative ring with one element and a free modulus of rank over

The definition can be formulated without using matrices as follows: Let ω be $\omega$ a determinant function. Then is $\det f$ determined by $f^{*}\omega =\left(\det f\right)\omega$ , where is $f^{*}$ the back transport of multilinear forms through be $\left(v_{1},\dotsc ,v_{n}\right)$ a basis of . Then holds:

$\det f:={\frac {\omega \left(f\left(v_{1}\right),\dotsc ,f\left(v_{n}\right)\right)}{\omega \left(v_{1},\dotsc ,v_{n}\right)}}$

It is $\det f$ choice of ω $\omega \neq 0$ and the basis. Geometrically interpreted, the volume of the $\left(f\left(v_{1}\right),\dotsc ,f\left(v_{n}\right)\right)$ spate spanned by obtained by calculating the volume of the spate spanned by $\left(v_{1},\dotsc ,v_{n}\right)$ $\det f$ multiplied by the factor

An alternative definition is the following: Let be the dimension of and Λ $\Lambda ^{n}V$ be the -th outer power of . Then there is a uniquely determined linear mapping Λ $\Lambda ^{n}f\colon \Lambda ^{n}V\to \Lambda ^{n}V$ , which is given by

$v_{1}\wedge \dotsb \wedge v_{n}\mapsto f\left(v_{1}\right)\wedge \dotsb \wedge f\left(v_{n}\right)$

is fixed. (This mapping Λ $\Lambda ^{n}f$ is obtained by universal construction as a continuation of onto the outer algebra Λ $\Lambda V$ restricted to the component of degree .)

Since the vector space Λ $\Lambda ^{n}V$ is one-dimensional, Λ $\Lambda ^{n}f$ simply multiplication by a body element. This body element is $\det f$ . It is therefore valid

$(\Lambda ^{n}f)(v_{1}\wedge \dotsb \wedge v_{n})=(\det f)\,v_{1}\wedge \dotsb \wedge v_{n}$ .

Further possibilities for calculation

Spat product

If a $3\times 3$ matrix is present, its determinant can also be calculated via the spar product.

Gaussian elimination method for determinant calculation

In general, determinants can be calculated with the Gaussian elimination method using the following rules:

If a triangular matrix, then the product of the main diagonal elements is the determinant of .
If results from by swapping two rows or columns, then $\det B=-\det A$ .
If results from by adding a multiple of one row or column to another row or column, then $\det B=\det A$ .
If results from forming the a row or column, then $\det B=c\cdot \det A$ .

Starting with any square matrix, use the last three of these four rules to transform the matrix into an upper triangular matrix, and then calculate the determinant as the product of the diagonal elements.

The determinant calculation by means of the LR decomposition is also based on this principle. Since both and are triangular matrices, their determinants result from the product of the diagonal elements, which are all normalised to 1 for According to the determinant product theorem, the determinant thus results from the relationship

$\det A=\det \left(L\cdot R\right)=\det L\cdot \det R=\det R=r_{1,1}\cdot r_{2,2}\dotsb r_{n,n}.$

Laplacian development theorem

With Laplace's development theorem, one can "develop" the determinant of an $n\times n$ matrix according to a row or column. The two formulas are

$\det A=\sum _{i=1}^{n}(-1)^{i+j}\cdot a_{ij}\cdot \det A_{ij}$ (development according to the -th column)

$\det A=\sum _{j=1}^{n}(-1)^{i+j}\cdot a_{ij}\cdot \det A_{ij}$ (development after the -th line),

where $A_{ij}$ is the $(n-1)\times (n-1)$ -submatrix of obtained by deleting the -th row and -th column. The product $(-1)^{i+j}\det A_{ij}$ is ${\tilde {a}}_{ij}$ called cofactor

Strictly speaking, the development theorem only gives a procedure for calculating the summands of the Leibniz formula in a certain order. In the process, the determinant is reduced by one dimension with each application. If desired, the procedure can be applied until a scalar results (see above).

Laplace's development theorem can be generalised in the following way. Instead of developing by only one row or column, one can also develop by several rows or columns. The formula for this is

$\det A=\sum _{|J|=|I|}(-1)^{\sum I+\sum J}\det A_{IJ}\det A_{I'J'}$

with the following designations: and are subsets of $\{1,\ldots ,n\}$ and $A_{IJ}$ is the submatrix of which consists of the rows with the indices of and the columns with the indices of and denote the complements of and . $\sum I=\sum \nolimits _{i\in I}i$ is the sum of the indices of . For the evolution by rows with indices from the sum runs over all $J\subseteq \{1,\ldots ,n\}$ where the number of these column indices |J| equal to the number of rows |I| evolve by. For the development according to the columns with the indices from the sum runs over . The number of summands is given by the binomial coefficient ${\binom {n}{k}}$ with k=|I|=|J| .

Efficiency:

The computational cost of Laplace's evolution theorem for a matrix of dimension $n\times n$ is of order ${\mathcal {O}}(n!)$ whereas the usual methods ${\mathcal {O}}(n^{3})$ are only of order and can sometimes be designed even better (see, for example, the Strassen algorithm). Nevertheless, Laplace's development theorem can be applied well to small matrices and matrices with many zeros.

Other properties

Determinant product theorem

The determinant is a multiplicative mapping in the sense that

for all $\det(A\cdot B)=\det A\cdot \det B$ $n\times n$ matrices and .

This means that the mapping $\det \colon \mathrm {GL} (n,K)\rightarrow K^{*}$ is a group homorphism from the general linear group into the unit group $K^{*}$ of the body. The kernel of this mapping is the special linear group.

More generally, the Binet-Cauchy theorem applies to the determinant of a square matrix that is the product of two (not necessarily square) matrices. Even more generally, a formula for the calculation of a minor of order product of two matrices results as a direct consequence of the Binet-Cauchy theorem. If an $m\times n$ matrix and is an $n\times p$ matrix and if $I\subseteq \{1,\ldots ,m\}$ and $J\subseteq \{1,\ldots ,p\}$ with |I|=|J|=k then the following applies with the same terms as for the generalised development theorem

$\det(A\cdot B)_{IJ}=\sum _{K\subseteq \{1,\ldots ,n\},|K|=k}\det A_{IK}\det B_{KJ}.$

The case m=p=k yields Binet-Cauchy's theorem (which becomes n=m the ordinary determinant product theorem for ) and the special case k=1 yields the formula for ordinary matrix multiplication.

Existence of the inverse matrix

→ Main article: Regular matrix

matrix A is invertible (i.e. regular) if $\det A$ a unit of the underlying ring (i.e. $\det A\neq 0$ for solids). If is invertible, then the determinant of the inverse is $\det \left(A^{-1}\right)=\left(\det A\right)^{-1}$ .

Similar matrices

→ Main article: Similarity (matrix)

If and are similar, that is, if there exists an invertible matrix such that $A=X^{-1}BX$ then their determinants coincide, because

$\det A=\det \left(X^{-1}BX\right)=\det \left(X^{-1}\right)\cdot \det \left(B\right)\cdot \det(X)=\det \left(X\right)^{-1}\cdot \det \left(B\right)\cdot \det \left(X\right)=\det B$ .

Therefore, independently of a coordinate representation, one can $f\colon V\to V$ define the determinant of a linear self-mapping (where a finite-dimensional vector space) by choosing a basis for describing the mapping by a matrix relative to this basis and taking the determinant of this matrix. The result is independent of the chosen basis.

There are matrices that have the same determinant but are not similar.

Block matrices

For the determinant of a $(2\times 2)$ block matrix

${\begin{pmatrix}A&B\\C&D\end{pmatrix}}$

with square blocks and one can, under certain conditions, give formulae which exploit the block structure. For B=0 or C=0 follows from the generalised development theorem:

This formula is also called a box set.

If is invertible, it follows from the decomposition

${\begin{pmatrix}A&B\\C&D\end{pmatrix}}={\begin{pmatrix}A&0\\C&1\end{pmatrix}}{\begin{pmatrix}1&A^{-1}B\\0&D-CA^{-1}B\end{pmatrix}}$

the formula

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(A)\det(D-CA^{-1}B).$

If is invertible, then it can be formulated:

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(D)\det(A-BD^{-1}C)$

In the special case that all four blocks have the same size and commutate in pairs, this results in the following with the help of the determinant product theorem

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC)=\det \left(\det _{R}{\begin{pmatrix}A&B\\C&D\end{pmatrix}}\right).$

Let $R\subseteq K^{n\times n}$ denote a commutative subring of the ring of all $n\times n$ matrices with entries from the body such that $\{A,B,C,D\}\subseteq R$ (for example, the subring generated by these four matrices), and let $\det _{R}\colon R^{2\times 2}\rightarrow R$ be the corresponding mapping that assigns its determinant to a square matrix with entries from This formula also holds if A is not invertible and generalises for matrices of $R^{m\times m}$ .

Eigenvalues and characteristic polynomial

Is the characteristic polynomial of the $n\times n$ matrix

$\chi _{A}(x):=\det(x\cdot E_{n}-A)$

$\chi _{A}(x)=x^{n}-a_{1}x^{n-1}+a_{2}x^{n-2}-\dotsb +(-1)^{n}a_{n}$ ,

then $a_{n}$ the determinant of .

Decomposes the characteristic polynomial into linear factors (with not necessarily different α $\alpha _{i}$ ):

$\chi _{A}(x)=(x-\alpha _{1})\dotsm (x-\alpha _{n})$ ,

so in particular

$\det(A)=\alpha _{1}\dotsm \alpha _{n}$ .

If λ $\lambda _{1},\dotsc ,\lambda _{r}$ are the different eigenvalues of the matrix with $r_{i}$ -dimensional generalised eigenspaces, then

$\det(A)=\lambda _{1}^{r_{1}}\dotsm \lambda _{r}^{r_{r}}$ .

Continuity and differentiability

The determinant of real square matrices of fixed dimension is a polynomial function $\det \colon \mathbb {R} ^{n\times n}\to \mathbb {R}$ , which follows directly from Leibniz's formula. As such, it is continuous and differentiable everywhere. Its total differential at the point $A\in \mathbb {R} ^{n\times n}$ can be represented by Jacobi's formula:

$D(\det A)H=\operatorname {spur} \left(A^{\#}H\right),$

where $A^{\#}$ denotes the matrix complementary to and $\operatorname {spur}$ denotes the trace of a matrix. In particular, for invertible that

$D(\det A)H=\det A\cdot \operatorname {spur} \left(A^{-1}H\right)$

or as an approximation formula

$\det \left(A+H\right)-\det A\approx \det A\cdot \operatorname {spur} \left(A^{-1}\,H\right),$

if the values of the matrix are sufficiently small. The special case when equal to the unit matrix results in

$\det \left(E+H\right)\approx 1+\operatorname {spur} H.$

Permanent

→ Main article: Permanent

The permanent is an "unsigned" analogue of the determinant, but is used much less frequently.

Generalisation

The determinant can also be defined on matrices with entries in a commutative ring with one. This is done with the help of a certain antisymmetric multilinear mapping: If is a commutative ring and $M=R^{n}$ the -dimensional free -module, then let

$f\colon M^{n}\to R$

the uniquely determined mapping with the following properties:

is -linear in each of the arguments.
is antisymmetric, i.e. if two of the arguments are equal, returns zero.
$f\left(e_{1},\ldots ,e_{n}\right)=1$ where $e_{i}$ is the element of having a 1 as -th coordinate and zeros otherwise.

A mapping with the first two properties is also called a determinant function, volume or alternating -linear form. The determinant is obtained by $R^{n\times n}$ identifying $M^{n}$ naturally with the space of square matrices

$\det \colon R^{n\times n}\cong M^{n}{\xrightarrow {f}}R$

Special determinants

Vronsky determinant
Pfaff determinant
Vandermonde determinant
Gram's determinant
Functional determinant (also called Jacobi determinant)
Determinant (knot theory)

History

Historically, determinants (Latin determinare "to delimit", "to determine") and matrices are very closely related, which is still the case according to our understanding today. However, the term matrix was only coined more than 200 years after the first thoughts on determinants. Originally, a determinant was considered in connection with systems of linear equations. The determinant "determines" whether the system of equations has a unique solution (this is precisely the case when the determinant is not equal to zero). The first considerations of this kind for $2\times 2$ matrices were carried out by Gerolamo Cardano at the end of the 16th century. About a hundred years later, Gottfried Wilhelm Leibniz and Seki Takakazu independently studied determinants of larger linear systems of equations. Seki, who tried to use determinants to give schematic solution formulas for systems of equations, found a rule for the case of three unknowns that corresponded to the later Sarrus rule.

In the 18th century, determinants became an integral part of the technique for solving systems of linear equations. In connection with his studies on intersections of two algebraic curves, Gabriel Cramer calculated the coefficients of a general conic section

$A+By+Cx+Dy^{2}+Exy+x^{2}=0,$

which runs through five given points and established Cramer's rule, which is named after him today. For systems of equations with up to four unknowns, this formula was already used by Colin Maclaurin.

Several well-known mathematicians such as Étienne Bézout, Leonhard Euler, Joseph-Louis Lagrange and Pierre-Simon Laplace were now primarily concerned with the calculation of determinants. An important advance in theory was achieved by Alexandre-Théophile Vandermonde in a work on elimination theory, completed in 1771 and published in 1776. In it, he formulated some fundamental statements about determinants and is therefore considered a founder of the theory of determinants. These results included, for example, the statement that an even number of permutations of two adjacent columns or rows does not change the sign of the determinant, whereas an odd number of permutations of adjacent columns or rows changes the sign of the determinant.

During his investigations of binary and ternary quadratic forms, Gauss used the schematic notation of a matrix without calling this number field a matrix. In the process, he defined today's matrix multiplication as a by-product of his investigations and showed the determinant product theorem for certain special cases. Augustin-Louis Cauchy further systematised the theory of the determinant. For example, he introduced the conjugate elements and clearly distinguished between the individual elements of the determinant and between the subdeterminants of different orders. He also formulated and proved theorems about determinants such as the determinant product theorem or its generalisation, Binet-Cauchy's formula. In addition, he made a significant contribution to the term "determinant" becoming established for this figure. Therefore, Augustin-Louis Cauchy can also be considered the founder of the theory of the determinant.

The axiomatic treatment of the determinant as a function of $n\times n$ independent variables was first given by Karl Weierstrass in his Berlin lectures (at the latest from 1864 and possibly already before), which Ferdinand Georg Frobenius then followed up in his Berlin lectures of the summer semester of 1874 and was, among other things, probably the first to systematically trace Laplace's development theorem back to this axiomatics.

Questions and Answers

Q: What is a determinant?

A: A determinant is a scalar (a number) that indicates how a square matrix behaves.

Q: How can the determinant of a matrix be calculated?

A: The determinant of the matrix can be calculated from the numbers in the matrix.

Q: How is the determinant of a matrix written?

A: The determinant of a matrix is written as det(A) or |A| in a formula.

Q: Are there other ways to write out the determinant of a matrix?

A: Yes, instead of det([a b c d]) and |[a b c d]|, one can simply write det [a b c d] and |[a b c d]|.

Q: What does it mean when we say "scalar"?

A: A scalar is an individual number or quantity that has magnitude but no direction associated with it.

Q: What are square matrices?

A: Square matrices are matrices with an equal number of rows and columns, such as 2x2 or 3x3 matrices.