Delta-v

Delta v () is the change (delta or Δ) in velocity (vector ) and is given in distance per time (m/s or km/h). It results from the subtraction of two velocities,

,

where is the velocity before an event and is the velocity after the event. Since Δ is calculated from the difference of the velocity vectors, changes in direction where the magnitude of the velocity remains the same are also taken into account.

Space Dynamics

In spaceflight, delta v, often written out rather than with formula symbols, is a measure of a spacecraft's ability to perform maneuvers. In the simplest case, without gravitational influence, delta v is the integral of the magnitudes of all velocity changes along the desired trajectory. This integral is invariant to the mass of the maneuvering spacecraft, as well as to technical details of its propulsion. The invariance of the quantity has obvious advantages, so that for spacecraft, instead of mass, thrust, and propellant supply, the total delta v () is given, of which the spacecraft is capable with the available propellant resources. If the value of the remaining Δ , all fuel is consumed and no course change is possible.

In the gravitational field, e.g. during launch or during a swing-by, the delta v to be applied by the spacecraft does not correspond directly to any change in velocity, but can nevertheless be calculated as a quantity. However, in the atmosphere and in a non-freefall situation, it additionally depends on the aerodynamic properties of the vehicle and the time required by the spacecraft to reach a stable orbit, i.e. a free-fall situation. For a launch into a Low Earth Orbit, about Δ is required to increase the velocity from the rotational velocity at the Earth's surface to the orbital velocity. This fraction is invariant to the spacecraft design. In addition, there is typically Δ due to air resistance and overcoming Earth gravity. The balance is reduced by the Earth's rotation by a maximum of 465 m/s if the launch is at the equator with an inclination of 0° in an easterly direction.

It should be noted that in this specification the weight of the payload (weight of the people on board / of the spacecraft) has an influence on the available delta v of a spacecraft, since with an increase in mass and thus increased inertia the available delta v becomes smaller. In other words, if the astronauts on the Apollo missions had packed too many moonstones, the required delta v of the ascent stage to reach the mother ship would remain the same, but the delta v that would be available would decrease and fall below the value of the required delta v, making the ascent stage too heavy and the mother ship no longer reachable.

For example, the Δ of the fully fueled Apollo spacecraft at maximum payload was 2,804 m/s, and that of the Lunar Module was 4,690 m/s.

Typical delta v for orbital and interplanetary maneuvers

Stabilization maneuvers	Rail height (km)	Delta v (m/s per year)
		type.	max.
Position stabilization		< 50–55
Height stabilization (air resistance)	< 400–500	<25	<100
	< 500–600	< 05	< 025
	>600		< 007,5

 

One-time maneuvers	Delta v (m/s)
Situation control	2–06
Rotation control	5–10
Relief of the position stabilisation gyroscope	2–06
Separation from the starting stage	5–10
Uncoupling a spacecraft from theISS by means of spring force	0,12

 

Maneuvers for orbit change (see graphic on the right)		Delta v (m/s)
From	to
Earth's surface	Low Earth Orbit (LEO)	9.300–10.000
Low Earth Orbit	Geostationary Transfer Orbit (GTO)	2.500
Geostationary transfer orbit	Geosynchronous Orbit (GEO, GSO)	1.500
Perigee of the geostationary transfer orbit	Escape Route	0.700
Escape Route	Low lunar orbit	0.700
	Mars Transfer Orbit	0.600
Low Earth Orbit	Surface of Mars	4.800
	Escape route from the solar system	8.700
Low lunar orbit	Lunar surface	1.600

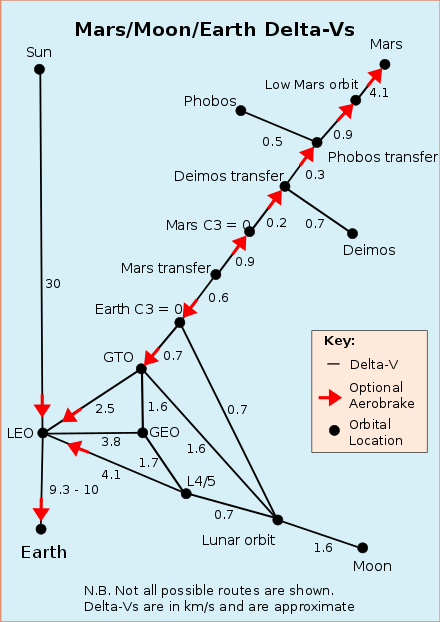
Delta v in km/s for various manoeuvres from the Earth to the Moon and Mars