Cylinder

A cylinder (Latin cylindrus, ancient Greek κύλινδρος kýlindros, from κυλίνδειν kylíndein 'to roll', 'to roll') is in the simplest case a

  • Surface whose points have the same distance from a fixed straight line, the raxis.

Since such a surface is infinitely extended, it is usually clipped with two parallel planes of distance h(see figure).

  • If the cut planes are perpendicular to the axis, the result is a perpendicular (or straight) circular cylinder with radius rand height h. The surface thus trimmed is called the cylinder's lateral surface, and the cut surfaces perpendicular to the axis can each be called the base surface.

Since a straight circular cylinder can also be thought of as being generated by the rotation of a line around the (parallel) cylinder axis, it is also called a rotating cylinder. The generating lines are called generatrixes of the cylinder or generatrixes.

In engineering, a cylinder is often understood to be the body enclosed by the lateral surface and the two intersecting circular surfaces.

In mathematics a cylinder is defined in a more general way (see section general cylinder)

Zoom

Vertical circular cylinder: height h, radius r

Circular cylinder

In practice, the vertical circular cylinder plays an important role in various variations. Therefore concrete formulas are given for this.

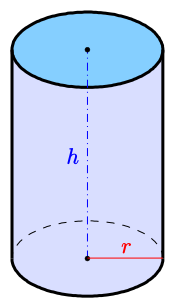
Vertical circular cylinder

This results in

  • the volume V=\pi \;r^{2}\;h\ ,(base area × height)
  • the lateral surface M=2\pi r\;h\ ,(the unwinding is a rectangle of length 2\pi rand height h)
  • the surface O=2\pi r^{2}+2\pi rh\ .

A straight circular cylinder with {\displaystyle h=2r}is called an equilateral cylinder. This name is explained as follows: If you intersect such a cylinder with a plane containing the cylinder axis, you get a square (with side length 2r).

If the cross section is an ellipse with semiaxes a,b, then

  • V=\pi ab\;h\ .There is no simple formula for the sheath area.

Hollow cylinder

If a straight circular cylinder has a bore along its axis, it is called a hollow cylinder. For a hollow cylinder - such as a straight piece of pipe - the determining quantities are, in addition to the height , hthe outer radius Rand the inner radius r. The wall thickness b is therefore R-r.

  • The volume is V=\pi R^{2}h-\pi r^{2}h=\pi (R^{2}-r^{2})\;h\ ,
  • the lateral surface (inner and outer) M=2\pi (R+r)\;h\ ,
  • the surface O=2\pi (R^{2}-r^{2})+2\pi (R+r)\;h=2\pi (R+r)(R-r+h)\ .

If the height hof a hollow cylinder is smaller than its outer radius Rwe speak of a perforated disc with a concentric, circular opening.

Cylinder section

If you intersect a straight circular cylinder (radius r) with a plane at an angle, the intersection curve is an ellipse. If the lower cylinder section has the minimum height h_{1}and the maximum height h_{2}then the intersection ellipse has

  • the major semiaxis a={\sqrt {r^{2}+({\tfrac {h_{2}-h_{1}}{2}})^{2}}}and the minor semiaxis {\displaystyle b=r}, where {\displaystyle {\tfrac {h_{2}-h_{1}}{2}}=r\tan {\beta }}, with β \beta the inclination angle of the section plane,
  • the numerical eccentricity ε {\displaystyle \varepsilon =\sin \beta }.

The cylinder section itself has

  • the volume {\displaystyle V=\pi r^{2}({\tfrac {h_{1}+h_{2}}{2}})},
  • the lateral surface {\displaystyle M=2\pi r({\tfrac {h_{1}+h_{2}}{2}})=\pi r(h_{1}+h_{2}),}
  • the surface {\displaystyle O=\pi (r^{2}+ar)+\pi r(h_{1}+h_{2})=\pi r(r+a+h_{1}+h_{2})}.

Note: The volume and the surface area are equal to those of the cylinder with mean height {\tfrac {h_{1}+h_{2}}{2}}.

Volume calculation of a lying circular cylinder (tank problem)

The calculation of the content V of a partially filled lying circular cylinder can be done using the length L, the radius rand the filling height h. According to the equation volume = base area - height given above, the volume of the filling is obtained by multiplying the area of the circle segment by the length Lthe cylinder:

V=r^{2}L\left(\arccos \left({\frac {r-h}{r}}\right)-(r-h){\frac {{\sqrt {2rh-h^{2}}}}{r^{2}}}\right).

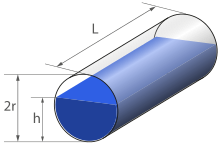
Partially filled horizontal cylinder (tank)Zoom
Partially filled horizontal cylinder (tank)

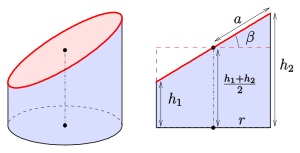
obliquely cut straight circle cylinderZoom
obliquely cut straight circle cylinder

Straight circular cylinder with unwound jacketZoom
Straight circular cylinder with unwound jacket

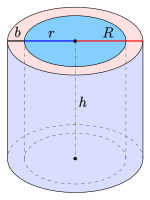
Hollow cylinderZoom
Hollow cylinder

General cylinder

In mathematics, one defines a cylinder (mantle) more generally:

  • A plane curve c_{0}in a plane ε \varepsilon _{0}is {\vec {a}}shifted along a straight line not \varepsilon _{0}contained in ε by a fixed distance Each two corresponding points of the curves c_{0}and the shifted curve c_{1} are connected by a line. The set of these parallel lines forms the associated cylinder surface (see figure). The curve c_{0}is called a directrix. A straight line lying on the cylinder is called the generatrix or generatrix line.

If the curve is a circle, the result is a skew circular cylinder. If {\vec a}\perp \varepsilon _{0}, the result is a perpendicular circular cylinder.

If c_{0}a closed curve, the surface with the two boundary surfaces can again be understood as the surface of a body. If the curve c_{0}not closed, e.g. a parabolic arc (see below), the cylinder is just the lateral surface explained above, which however can be part of a surface of a body.

The geometrical peculiarity of a cylindrical surface consists in the following fact:

  • A cylindrical surface contains straight lines, it is a ruled surface, and can be unwound into the plane without distortion.

This property in particular makes the cylinder surface interesting for the manufacture of sheet metal cladding.

  • If the generating curve is a polygon, it is called a prism (see examples).
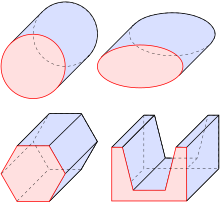
Examples of cylinders: circular cylinder and elliptical cylinder above, elliptical cylinder below: PrismsZoom
Examples of cylinders: circular cylinder and elliptical cylinder above, elliptical cylinder below: Prisms

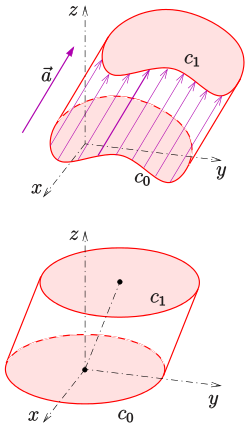
Definition of a general cylinder and example of an oblique circular cylinderZoom
Definition of a general cylinder and example of an oblique circular cylinder

Questions and Answers

Q: What is a cylinder?


A: A cylinder is a three dimensional geometric shape with the surface formed by points at a fixed distance from a given line segment, known as the axis of the cylinder. It can be thought of as a circular prism and both the surface and solid shape created inside can be called a cylinder.

Q: How long have people known about the surface area and volume of cylinders?


A: The surface area and volume of cylinders have been known since ancient times.

Q: What are elliptic, parabolic, and hyperbolic cylinders?


A: Elliptic, parabolic, and hyperbolic cylinders are cylinders whose cross section is an ellipse, parabola, or hyperbola respectively.

Q: How is a cylinder defined in differential geometry?


A: In differential geometry, a cylinder is defined more broadly as a ruled surface which is spanned by a one-parameter family of parallel lines.

Q: What does it mean for something to be "ruled"?


A: To be "ruled" means that it has straight lines drawn on it in some way or another.

Q: Is there only one type of cylinder?


A: No, there are many different types of cylinders such as elliptic, parabolic, and hyperbolic cylinders which all have different cross sections.

AlegsaOnline.com - 2020 / 2023 - License CC3