Cuboid

The title of this article is ambiguous. For other meanings, see cuboid (disambiguation).

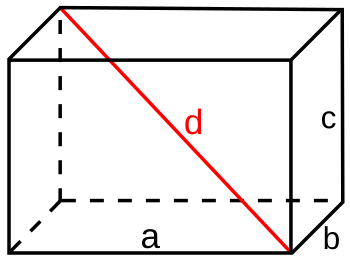
A cuboid is a geometric solid bounded by 6 rectangles.

A cuboid has

6 rectangular side faces that are at right angles to each other,
8 right-angled corners and
12 edges, four of which have equal lengths and are parallel to each other.

Opposite faces of a cuboid are parallel and congruent (congruent). The cuboid is a rectangular three-dimensional parallelepiped.

In the special case of equal edge lengths a=b=c , where all faces of the square are squares, the result is a cube. In the case where exactly two edge lengths are equal, for example $a=b\neq c$ the result is a square straight prism, sometimes called a square plate ( a=b>c ) or a square column ( a=b<c ).

Cuboid with space diagonal d

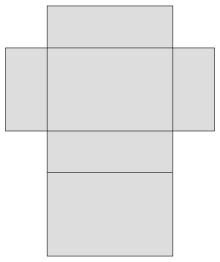
Unfolded net of a cuboid

Symmetry

Cuboids have several symmetry properties depending on the number of equal edge lengths.

have cuboids with three different edge lengths

3 bidentate axes of rotation (through the midpoints of two opposite faces),
3 mirror planes (3 planes through four edge centers each),
3 rotational reflections (by 180° with the planes through four edge centers each)

cuboids with two different edge lengths (square straight prisms) have

1 fourfold axis of rotation (through the centers of two opposite squares),

2 bidentate axes of rotation (through the midpoints of two opposite rectangles),
3 rotational reflections (by 180° with the planes through four edge centers each)

Cuboids with only one edge length, the cubes, have more symmetries (see cubes - symmetry).

Each cuboid is

point-symmetrical to the center M.

Formulas

Sizes of a cuboid with edge lengths a, b, c
Volume	$V=a\cdot b\cdot c$
Sheathing	$A_{M}=2\cdot (a+b)\cdot c$
Surface area	$A_{O}=2\cdot (a\cdot b+a\cdot c+b\cdot c)$
Circumferential radius	$r_{u}={\tfrac {d}{2}}={\tfrac {1}{2}}\cdot {\sqrt {a^{2}+b^{2}+c^{2}}}$
Space diagonal	$d=2\cdot r_{u}={\sqrt {a^{2}+b^{2}+c^{2}}}$
Area diagonals	$d_{a}={\sqrt {b^{2}+c^{2}}}$
	$d_{b}={\sqrt {c^{2}+a^{2}}}$
	$d_{c}={\sqrt {a^{2}+b^{2}}}$
Volume to sphere volume ratio	${\frac {V}{V_{UK}}}={\frac {6\cdot a\cdot b\cdot c}{\pi \cdot (a^{2}+b^{2}+c^{2})^{\frac {3}{2}}}}$
Solid angle in the corners	$\Omega ={\frac {\pi }{2}}\;\mathrm {sr} \;\approx 1{,}5708\;\mathrm {sr}$

Optimization problems and the cube

There are several optimization problems for cuboids. If one is looking for a cuboid which is

given length of the diagonal or given sphere volume the maximum surface area
given length of the diagonal or given sphere volume the maximum volume
given surface area the minimum length of the diagonal or the minimum volume of the sphere
given surface area the maximum volume
given volume the minimum length of the diagonal or the minimum sphere volume
given volume the minimum surface area

then the solution in each case is the cube.

In each case, two of the six optimization problems are basically the same problem with other given sizes, so that there are actually only three different optimization problems. For the optimization problems mentioned, the cube is the cuboid we are looking for. Of course, this is not true for all optimization problems.

That the optimization problems for the length of the diagonal and the circumsphere volume $V_{UK}$ each have the same solution is obvious, because the circumsphere volume $V_{UK}={\frac {4}{3}}\cdot \pi \cdot r_{u}^{3}={\frac {1}{6}}\cdot \pi \cdot d^{3}$ is a continuous and strictly monotonically increasing function with function variable

cuboid with the largest volume is sought for a given circumsphere radius, then the edge lengths , , of the cuboid using the partial derivatives of the volume function $V(a,b)=a\cdot b\cdot c=a\cdot b\cdot {\sqrt {d^{2}-a^{2}-b^{2}}}=a\cdot b\cdot {\sqrt {4\cdot r_{u}^{2}-a^{2}-b^{2}}}$ compute or with proof by contradiction:

Suppose that any cuboid with at least two different edge lengths, for example and , would have the largest volume. Its circumspherical radius is ${\frac {1}{2}}\cdot {\sqrt {a^{2}+b^{2}+c^{2}}}$ and its volume $a\cdot b\cdot c$ . Then another cuboid, namely the cuboid with edge lengths ${\frac {1}{2}}\cdot {\sqrt {2\cdot a^{2}+2\cdot b^{2}}}$ , ${\frac {1}{2}}\cdot {\sqrt {2\cdot a^{2}+2\cdot b^{2}}}$ and the same circumsphere radius ${\frac {1}{2}}\cdot {\sqrt {a^{2}+b^{2}+c^{2}}}$ and the volume ${\frac {a^{2}+b^{2}}{2}}\cdot c$ . Because of the inequality from the arithmetic and geometric mean ${\sqrt {a\cdot b}}\leq {\frac {a+b}{2}}$ , because $a\neq b$ and $c>0$ holds $a\cdot b<{\frac {a^{2}+b^{2}}{2}}$ and $a\cdot b\cdot c<{\frac {a^{2}+b^{2}}{2}}\cdot c$ .

So the arbitrary cuboid with at least two different edge lengths cuboid has a smaller volume than the other cuboid. From this follows that a cuboid with at least two different edge lengths cannot have the largest volume and finally that the cuboid with only one edge length, i.e. the cube with 12 edges of equal length, has the largest volume of all cuboids with a given radius of revolution.

Decisive for this proof by contradiction is here that the volume of the cuboid must be finite, because it is obviously smaller than the volume of the circumsphere, and that the volume function is continuous.

Cuboid

Symmetry

Formulas

Optimization problems and the cube

Search by letter