Cross product
This article is about the product of two vectors in space; for other meanings, see Cross product (disambiguation).
The cross product, also known as vector product, vectorial product, or outer product, is a linkage in three-dimensional Euclidean vector space that assigns a vector to two vectors again. To distinguish it from other products, especially the scalar product, it is written in German- and English-speaking countries with a paint cross 
as multiplication sign (see section Spellings). The terms cross product and vector product go back to the physicist Josiah Willard Gibbs, the term outer product was coined by the mathematician Hermann Graßmann.
The cross product of the vectors 
and 
is a vector perpendicular to the plane spanned by the two vectors and forms a right system with them. The length of this vector is equal to the area of the parallelogram spanned by the vectors and
In physics, the cross product occurs in many places, for example in electromagnetism when calculating the Lorentz force or the Poynting vector. In classical mechanics, it is used for angular quantities such as torque and angular momentum, or for apparent forces such as the Coriolis force.
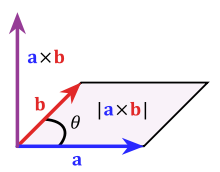
Cross product
Geometric definition
The cross product 
of two vectors and in three-dimensional visual space is a vector orthogonal to and , and hence orthogonal to the plane spanned by and
This vector is oriented such that 
and form a right system in that order. Mathematically, this means that the three vectors and are oriented the same as the vectors 
, 
and 
the standard basis. In physical space, it means that they behave like the thumb, index finger and splayed middle finger of the right hand (right-hand rule). Rotating the first vector into the second vector yields the positive direction of the vector via the right-hand screw sense.
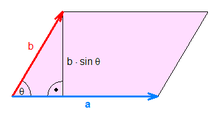
The magnitude of gives the area of the parallelogram spanned by and . Expressed by the angle θ enclosed by and 
holds that
Where 
and 
denote the lengths of the vectors and , and 
is the sine of the angle θ enclosed by them .
In summary
where the vector 
is the unit vector perpendicular to and that completes them to a right system.
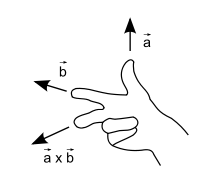
Right hand rule
Spellings
Depending on the country, different notations are used for the vector product. In English and German-speaking countries, the vector product of two vectors and is usually written as , whereas in France and Italy the notation 
preferred. In Russia, the vector product is often ![{\displaystyle [{\vec {a}},{\vec {b}}]}](https://www.alegsaonline.com/image/008d8868e90625dc41200b2396382596923b8d9c.svg)
notated as ![{\displaystyle [{\vec {a}}\ {\vec {b}}]}](https://www.alegsaonline.com/image/f525d35f8edddf7a3f90c4d8666e165cc0ac5a00.svg)
or .
The notation and the term outer product are used not only for the vector product, but also for the conjunction that assigns a so-called bivector to two vectors, see Graßmann algebra.
Questions and Answers
Q: What is the cross product?
A: The cross product is a mathematical operation that can be done between two three-dimensional vectors.
Q: How is the cross product often represented?
A: The cross product is often represented by the symbol × or \times.
Q: What happens after performing the cross product?
A: After performing the cross product, a new vector is formed.
Q: What is the relationship between the cross product vector and the vectors that were "crossed"?
A: The cross product of two vectors is always perpendicular (it makes a corner-shaped angle) to both of the vectors which were "crossed".
Q: In what dimension does the cross product normally work?
A: Cross product normally works only in three-dimensional space.
Q: What are the three dimensions where cross product can be performed?
A: The three dimensions where cross product can be performed are up or down, left or right, and forward or backwards.
Q: Why can cross product normally only work in three-dimensional space?
A: Cross product normally works only in three-dimensional space because those are the dimensions where you can go up or down, left or right, and forward or backwards.
