Cosmic distance ladder

Distance measurement, distance measurement or length measurement is the measurement of the distance between two points in space by direct or indirect comparison with a unit of length such as the meter. Optical distance meters are also called telemeters.

The range of possible lengths begins with the so-called Planck length of about 10-35 meters. This is the smallest length into which space can be divided. The physically relevant range begins at 10-18 meters, the size of elementary particles, and extends to 1026 meters. It thus spans 44 decimal orders of magnitude - from atomic physics to biology and technology to the most distant galaxies. This means that a very large number of different methods are needed to measure distances.

Combining distance and direction measurement, the position of points in a plane or spatial coordinate system can be determined - see geometry, surveying, positioning, navigation and astrometry.

The following diagram gives an overview of the unit prefixes for length and distance measurements, contains examples for the size ranges and assigns the respective measuring principles.

Measurement principles

Direct measurement

The most direct form of distance measurement is the so-called direct measurement. This is the direct comparison of the distance to be determined with a scale. This type of measurement is only possible in a limited length range, since comparison scales cannot be produced in any size. The smallest scales are produced using lithographic methods and are only a few micrometers in size. They can be used under a microscope like a normal tape measure or are read automatically with optical devices (see glass scale). The longest scales are made of flexible steel tape in lengths up to more than 100 meters.

All these scales are traced back to a length standard (formerly the primal metre, today the definition of the metre with the help of the light transit time). This process is called calibration. The definition of the metre enables the worldwide comparability of length measurements.

From a computational point of view, the direct distance measurement is to be treated as an oblique distance, which still requires the measurement of its inclination or the elevation angle for its conversion into a horizontal distance.

In the following, some methods of direct distance measurement are listed and briefly explained.

Interferometry

Interferometry with coherent waves is very precise in the measurement of length changes. The accuracy depends mainly on the wavelength used. In practice, light and radio waves are used. In order to be able to measure distances with an interferometer, the phase shift method, white light interferometry or also conoscopic holography are used, among others. Interferometry is a direct measurement technique, since the distance to be determined is compared with the wavelength of the light used. The wavelength is linked to the international system of units.

Confocal distance measurement

Confocal technology is used in various technical designs to determine very small distances in the nanometer to millimeter range. It is based on the effect of depth discrimination: a confocal sensor delivers a signal that is greater the closer the measurement object is to the focal plane of the optics. The confocal technique is a direct measurement, as it shifts the object or optics by the measuring length and compares the shift with a reference scale.

Indirect measurement

Direct measurement cannot be used in many cases. It already fails when determining the distance between two islands from the mainland, since the two points are not accessible at the same time. Indirect methods are more universal and usually more convenient to use.

All indirect methods have in common that they do not measure the distance itself, but a quantity dependent on it - for example the transit time measurement of a signal or echo (laser, radar), the direction of a bearing or the brightness of a star. Indirect measurements are also used to measure any changes in distance, for example by means of the Doppler effect. Indirect measurements must be calibrated by comparison with known scales to ensure comparability with other measurements.

Hodometry

Hodometry, often referred to as odometry, is a very simple and old method of indirect distance measurement, which can also be used to a limited extent for distance measurement. It involves counting the revolutions of a wheel of known circumference that is rolled along the measured distance. The number of revolutions multiplied by the circumference gives the measured distance. In everyday life, this method is used, for example, for odometers of cars or measuring wheels in surveying.
(See also: Curvimeter, device for measuring curved distances on maps).

Inertial Navigation

Inertial navigation is based on the fact that a movement which is not uniform is always associated with an acceleration of the moving object. If all accelerations experienced by an object are integrated over time as a function of direction, the distance travelled can be calculated from this using the simple formula of velocity equals acceleration times time and distance equals velocity times time (twofold numerical integration). This method is used in all types of vehicles and aircraft to enable distance measurement independent of the environment. However, measurement errors accumulate over time, which is why the position must be compared with information from other sources at regular intervals.

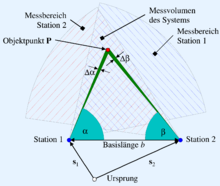
Triangulation

Triangulation was already used in ancient times for land surveying and is still used for this purpose today, except for technical innovations. The measuring method itself uses direct or indirect angle measurements to the measuring point with a known length of the measuring base. The distance to the base can be calculated from the spatial position of two angles.

In triple angulation or triangulation, the sought measurement point is aimed at from at least two different locations at a known distance using a theodolite or other protractor. The object point P and the two viewpoints (1 and 2) form a triangle whose base length and whose base angles α $\alpha$ and β $\beta$ are known. This can be used to calculate all other quantities in the triangle. The base length is the scale of the triangulation. The three angles of the triangle give the method the name 'triangulation'.

${\tfrac {b}{\sin(180^{\circ }-\alpha -\beta )}}={\tfrac {\overline {BP}}{\sin \alpha }}={\tfrac {\overline {AP}}{\sin \beta }}$

Optical rangefinders that work according to this principle are the coincidence and spatial image rangefinder. In a reversal of this procedure, the end points of a highly accurate reference distance, a so-called base plate, can also be aimed at from one point. The base plate thus forms the base length of an isosceles triangle.

In addition, optical measurement techniques such as fringe projection and photogrammetry have opened up other areas of application.

Distance sensors also use the principle of triangulation (see laser triangulation).

A simple variant for estimating distances without technical aids is the leap of the thumb. It only requires that you know the approximate size of the target object.

Trilateration

Trilateration is a method similar to triangulation, which also uses three quantities of a triangle to describe it, namely its sides. From this, in turn, all other quantities that define the triangle can be calculated.

The measuring method itself uses direct or indirect (radio-technical) distance measurements, realized metrologically in each case as time-of-flight measurements (unambiguous) or additionally by phase comparisons (ambiguous). From the spatial position of two points, their distance can be calculated on the basis of geometric relationships in the triangle. The method serves primarily to determine the spatial position of measuring points to each other on the basis of simple distance measurements quickly and with sufficient accuracy.

Four known points are required to determine the location of an unknown point in three-dimensional space, three known points are sufficient on a surface and two known points are sufficient along a trajectory. If it is possible to choose between several mathematically correct solutions on the basis of constraints, the number of necessary known points can be reduced by the number of usable constraints.

Trilateration is the basis of distance measurement, for example in satellite navigation systems or in Global Navigation Satellite Systems. In the sense of classical geodesy, trilateration is not an independent surveying method, but it is in satellite geodesy (see also Satellite Laser Ranging and SECOR).

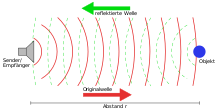
Runtime measurement

Time-of-flight measurement is based on the fact that electromagnetic and acoustic waves propagate at a finite, known speed. If you send a signal to an object from which it is reflected and measure the time it takes to travel there and back, you can calculate the object distance from the travel time Δ $\Delta t$ and the propagation speed of the signal, which is the group velocity of the wave:

$r={\frac {c\cdot \Delta t}{2}}$

The measurements are influenced by the environment. If a medium is penetrated, the speed of light is reduced compared to the speed of light in a vacuum. If the material properties are temperature-dependent or anisotropic tensors, measurements of the transit time are disturbed by changes in the parameters or orientation. For example, the speed of sound is strongly temperature dependent, electromagnetic waves are deflected by electrically conducting layers of the atmosphere.

The determination of the walking path is particularly problematic: Only direct walking paths provide the direct distance. All detours via secondary reflectors provide longer travel times and thus incorrect measurement data.

Examples:

Bats and ultrasonic distance sensors or meters use ultrasonic signals to determine the distance of obstacles and prey.
The echo sounder and sonar use sound signals in the water for depth measurement under ships, for distance measurement under water (submarines) and for locating schools of fish.
Radar systems use electromagnetic waves in the radio wavelength range to measure distances. A distinction is made between pulse radars for long distances and continuous wave radars for short distances. See e.g. Distance Measuring Equipment, Satellite Navigation (e.g. GPS), Time Domain Reflectometry.
Light is also suitable for this method, see Satellite Laser Ranging, LIDAR, laser gun, electro-optical ranging.
A similar principle is used in radio navigation (especially hyperbolic navigation), when the differences in propagation time of signals transmitted in a coordinated manner from different fixed transmitters to a receiver whose position is to be determined are converted into differences in distance.

Chromatic-confocal distance measurement

Chromatic-confocal distance measurement uses the dispersion of white, i.e. spectrally broadband, light in an optical system to determine the distance between the measurement object and the sensor. The different focal lengths for different spectral components of the sensor light due to the dispersion in the focus lens are used for the measurement.

Capacitive distance measurement

The distance between two conductive parts can be determined by the capacitance existing between them. For this purpose, the parts must be insulated from each other; for capacitance measurement, they are included in an electric oscillating circuit or a ring oscillator whose frequency depends sensitively on the capacitance. Applications include focus position control on laser cutting machines, position control in nanopositioning systems and force measurement.

Parallax

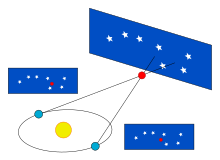
Various parallax methods are used to determine distances beyond the scale of the solar system. The word "parallax" is used here in the sense of "distance". A distinction is made between the following:

Trigonometric parallax

The trigonometric parallax is the change in the direction of view to an object with respect to the celestial background caused by the annual motion of the Earth around the Sun. The trigonometric parallax is thus based on triangulation, its base length being the diameter of the Earth's orbit. In addition, we also speak of diurnal parallax, which is caused by the rotation of the Earth. The further away the object is, the smaller the parallax. From it, the distance can be calculated directly:

$r=1/\pi$

where here the distance r is in parsecs (pc) and the parallax π is $\pi$ in arcsecs.

The first parallax measurement of a star could be done in 1838 by Friedrich Wilhelm Bessel for the star 61 Cygni. He determined a value of about 0.3 arc seconds and thus a distance of about 3.3 pc. Proxima Centauri, the star closest to Earth, has a parallax of 0.762 arcseconds, corresponding to a distance of about 1.31 pc. Normally, the trigonometric parallax can be determined up to distances of about 100 pc. With modern methods, however, parallaxes of a few milliarcseconds have been measured today. Between 1989 and 1993 the satellite Hipparcos measured about 100,000 stars up to a magnitude of 9 mag and determined their parallaxes. It achieved an error of only 0.001 arcseconds. The smallest parallax so far (2005) could be determined for the pulsar PSR B1508+55 with a radio telescope: it was 0.415 milliarcseconds (=0.000415 arcseconds) - this corresponds to a distance of about 2,400 pc or about 7,800 light-years.

Spectroscopic parallax

With spectroscopic or photometric parallax, it is not the direction of the light that is examined, as with trigonometric parallax, but its quality. In addition to the temperature of a star, the intensity of the light arriving at Earth naturally depends on the distance, which also makes it possible to measure the distance. Of course, the brightness of a star that can be observed directly is only the so-called apparent brightness m. A very bright star that is far away and a very close star that shines dimly can both appear equally bright to an earthly observer. Therefore, it is necessary to define the absolute magnitude M: it corresponds to the apparent magnitude that an object would have if it were exactly 10 pc from the Earth. The relationship between apparent and absolute magnitude is as follows:

$m-M=-5+5\cdot \log r$

where the distance r must be given in parsecs. If the absolute magnitude of an object is known, the distance can be calculated immediately from the measured apparent magnitude. The absolute magnitude can be determined by comparing spectra. Here, the spectrum of an object with a known distance is used as a benchmark - i.e. the spectroscopic parallax builds directly on the trigonometric parallax.

Dynamic parallax

The dynamic parallax is used to determine the distance of visual double stars. For this, the orbital velocity , which can be determined spectroscopically, must be known; from the apparent distance of the two stars and the orbital period of the stars around their center of mass, one can now calculate the distance

Redshift

Distance determination using the redshift of light is used for very distant objects such as galaxies or quasars. For these distances, no alternative measurement methods are available. For redshift, known spectral lines in the spectrum of a galaxy must be identified and their exact wavelength measured. The distance can be calculated using the Hubble constant $H_{0}$ with the following formula:

$r={\frac {z\cdot c}{H_{0}}}$

Where $z={\frac {\lambda _{{\text{beobachtet}}}-\lambda _{0}}{\lambda _{0}}}$ is the redshift and is the vacuum light speed.

It should be noted that the value of the Hubble constant cannot be determined precisely at present and used to be subject to strong fluctuations. The latest measurements give values - depending on the measurement method - between 68 and 74 ${\frac {\mathrm {km} }{\mathrm {s\cdot Mpc} }}$ .

Origin of the parallax during the orbit of the earth around the sun

Principle of the runtime measurement

Principle of triangulation

Measuring wheel

Distance measurement in the military (1903)

Questions and Answers

Q: What is the cosmic distance ladder?

A: The cosmic distance ladder is the method used by astronomers to measure the distance of objects in space.

Q: Why do astronomers use a number of methods to measure distances in space?

A: No one method works for all objects and distances, so astronomers use a number of methods.

Q: Is direct distance measurement of astronomical objects possible for all objects?

A: No, direct distance measurement is only possible for objects that are close enough to Earth (within about a thousand parsecs).

Q: What is a standard candle?

A: A standard candle is an astronomical object that has a known standard luminosity.

Q: Why is the analogy to a ladder used for the cosmic distance ladder?

A: The analogy to a ladder is used because no one technique can measure distances at all ranges encountered in astronomy, instead one method can be used to measure nearby distances, and each rung of the ladder provides information that can be used to determine the distances at the next higher rung.

Q: What does each rung of the cosmic distance ladder provide?

A: Each rung of the cosmic distance ladder provides information that can be used to determine the distances at the next higher rung.

Q: What is the extragalactic distance scale?

A: The extragalactic distance scale is another term for the cosmic distance ladder used by astronomers to measure the distance of objects in space.