Coriolis force

The Coriolis force ([kɔrjoˈliːskraft]) is one of the three inertial forces of classical mechanics that occur in a rotating reference frame. The Coriolis force appears precisely when the body is moving in the rotating reference frame and when this motion is not parallel to the axis of rotation or the vector of angular velocity. The Coriolis force is perpendicular to the instantaneous direction of motion of the mass point in the rotating reference frame and therefore does not cause an increase or decrease in its velocity, but a deflection to the side. The Coriolis force on a mass point is proportional to its mass and to the speed with which it moves in the rotating reference frame, as well as to the angular velocity with which the reference frame rotates. The location of the body, on the other hand, is irrelevant, especially since the vectorial angular velocity, which is the only thing that matters here, is independent of the location of a reference point or an axis of rotation.

The other two inertial forces in the rotating reference frame, centrifugal force and Euler force, also act when the body is at rest in the rotating reference frame.

In an earth-fixed reference system, only the Coriolis force appears. It has a decisive influence on large-scale flow phenomena. Examples from meteorology are the directions of rotation of the wind fields around high and low pressure areas and the formation of global wind systems such as trade winds and jet streams. In oceanography, the Coriolis force has a significant influence on ocean currents. For example, it directs cold currents along the Pacific coast of North and South America, which affects the climate there. Only the component of the Coriolis force parallel to the Earth's surface plays a significant role, which is why it is often simplified in the geosciences as "the Coriolis force". Its strength depends on the geographical latitude. It disappears at the equator and is strongest at the poles.

The widespread thesis that the Coriolis force is responsible for the direction of rotation of small whirlpools such as those in the bathtub and sink is not true. In engineering, the Coriolis force, in addition to the centrifugal force, must be taken into account for all movements that take place relative to a rotating base, e.g. when the two parts of a robot arm move simultaneously, or when the jib of a construction crane swivels and at the same time the trolley moves inwards or outwards. The same is true when you want to walk on the devil's wheel. These and other manifestations of the Coriolis force in rotating systems are also called the Coriolis effect. The Coriolis force here is to be understood as part of the inertial resistance with respect to the external force causing the motion.

The Coriolis force was first correctly derived by Pierre-Simon Laplace in 1775. However, it is named after Gaspard Gustave de Coriolis, who treated it in detail in a publication published in 1835.

A hurricane that develops with the participation of the Coriolis force

Introduction

An explanation of the Coriolis force, which tries to make do with everyday words and without relevant prior knowledge, could be as follows:

Only a force can change the instantaneous speed of a body according to amount or direction, because out of itself it always "wants" to move straight-line-similarly. Now, if one wants to go to the center on a turntable on a painted straight line, the motion will appear straight only as seen from the turntable, but curved from the solid ground outside the turntable. This second judgement by a non-moving observer is decisive here. So to go straight ahead on the disk anyway, it takes the force from the side necessary for any curved motion. If one is prepared for this, one will bring up this force, similar to bracing oneself against a strong side wind. To the walker, it feels as if he must apply this force against something that will distract him. This something is called the Coriolis force.

To be more precise: In a rotating reference frame, for example in one connected to a rotating disc, it can be stated that a body on which no external force acts does not move uniformly in a straight line according to the principle of inertia, but in addition to centrifugal acceleration is also always deflected perpendicular to the direction of motion. Its track is bended, thus it performs an accelerated movement. The portion of this acceleration that is perpendicular to the direction of motion and proportional to both the relative velocity on the disk and the angular velocity of the reference frame is called the Coriolis acceleration and is interpreted as the effect of a corresponding force, the Coriolis force. Similarly, it is found that a real external force of equal strength but opposite direction must act if motion relative to a rotating reference frame is to be rectilinear.

This effect is made tangible at the so-called "devil's wheel" at fairs. People are asked to walk on a rotating disc, e.g. along a painted straight line radial to the centre. Forces are necessary for this movement, as it is not a straight-line movement when viewed from the outside. As the orbital speed of the disc decreases as it moves inwards, the walker must apply a force against the direction of rotation prevailing at his location in order to slow his body down accordingly. He must also apply a force of the same direction and strength to continue turning the direction of his motion accordingly. Since the sum of these two forces and the Coriolis force exactly cancel each other out, the Coriolis force is the inertial resistance with respect to the transverse force to be applied by the runner. Since in these conditions the centrifugal force and the Coriolis force are perpendicular to each other, they can be distinguished by the walker even if the disc did not allow an outward view. The appearance of external forces in a uniform motion is thus evidence that one is not in an inertial frame.

In a well-known demonstration experiment on the Coriolis effect, a ball is made to roll as frictionlessly as possible over a rotating disc. Seen from outside the disk, the ball rolls in a straight line, because it moves uniformly due to its inertia (in the animation, the straight yellow track on the disk shown above). From the point of view of a camera fixed to the disc, the ball does not reach the red point as expected, but is deflected sideways against the direction of rotation of the disc. This deflection is the result of the Coriolis force. Its component in the circumferential direction is constant during the process, since the radius also increases at a constant speed. The deviation from the aimed target grows, measured on the arc (arc length between the sphere and the red point in the animation) in the form of a uniformly accelerated movement.

If we denote by ω ${\vec {\omega }}$ the vectorial angular velocity of the reference frame, the magnitude of which indicates how fast the reference frame is rotating, and by ${\vec v}'$ the velocity with which the body is moving in the reference frame, then the Coriolis acceleration is calculated ${\vec {a}}_{C}$ quite generally according to the formula

${\vec {a}}_{\mathrm {C} }=-2\,{\vec {\omega }}\times {\vec {v}}'$ .

The present article follows this definition of sign, which is now commonly used in physics. The conjunction of the quantities ω ${\vec {\omega }}$ and ${\vec v}'$ is $\times$ expressed by the cross product with the symbol The three vectors ω ${\vec {\omega }}$ , ${\vec v}'$ and ω ${\vec {\omega }}\times {\vec {v}}'$ thereby form a system of laws. To illustrate it, one can use the so-called "three-finger rule".

In analogy to Newton's second law, physics assumes that the cause of this acceleration is a force proportional to it, the Coriolis force, which is the product of the mass of the body and the Coriolis acceleration. However, since there is no physical cause for this force and also no other body on which it acts back, it is called a fictitious force or apparent force.

${\vec {F}}_{\mathrm {C} }=m\,{\vec {a}}_{\mathrm {C} }=-2\,m\,{\vec {\omega }}\times {\vec {v}}'$

The direction of the resulting vector ${\vec F}_{{\mathrm {C}}}$ is perpendicular to both the instantaneous direction of motion and the axis of rotation of the reference system. Therefore, the Coriolis force is always in a plane perpendicular to the axis of rotation, and is zero for motions parallel to the axis of rotation. If, as a co-rotating observer, one looks against the direction of the angular velocity, i.e. perpendicular to the counterclockwise rotating plane, the body is always deflected to the right, regardless of whether it is moving towards or away from the axis or around it.

Centrifugal and Coriolis forces influence the motion sequences on the "devil's wheel".

Movement of a body from the centre of a rotating disc outwards without friction; above: in the stationary reference frame, the body moves uniformly in a straight line; below: in the co-rotating reference frame (disc), the body moves along a spirally curved path.

Illustrative derivation

The following considerations, which make the phenomenon approximately comprehensible on the basis of finite intervals in time and space, yield an exact justification of the Coriolis force in the limiting case of infinitesimally small intervals.

Simple example

The uniform rectilinear motion of a force-free body is described from a rotating (x',y') coordinate system. At time t=0 , let the body be at $(x',y')=(0,0)$ , and let the axis lie straight in its direction of motion. At time , when the body $r=v\,t$ has travelled the distance this axis has $\omega \,t$ rotated by the angle ω so that it is now at a distance $y'=r\sin \omega \,t$ from the body flying straight ahead. For small times $\sin \omega \,t\approx \omega \,t$ , so the distance grows quadratically: $y'\approx v\omega t^{2}$ . From the rotating reference frame, the force-free body thus moves uniformly accelerated perpendicular to the original direction of motion according to the law $y'={\tfrac {1}{2}}at^{2}$ . The acceleration $a=2v\omega$ is the Coriolis acceleration.

Accordingly, if the body is instead to move along the rotating axis, it cannot be force-free, but must be accelerated in $F=2mv\omega$ the direction by an external force of strength The Coriolis force is the inertial resistance to this acceleration.

Strictly speaking, this simple derivation is only valid for the infinitesimal environment of the center, where the geometric description by straight and mutually perpendicular short distances is exact in the limit case. However, it also covers the general case where the body does not begin its motion with respect to the rotating reference system at its origin, but at an arbitrary starting point. One can describe the momentary motion of the reference system just as well by choosing this starting point as the center of rotation and additionally allowing a translation of the reference system. The angular velocity remains unchanged according to amount and direction, the relative velocity too, and thus also the Coriolis force.

For an explicit description of the conditions at arbitrary starting points on the turntable see the following sections. For the further motion of the body outside the infinitesimal proximity of the starting point, see the derivation of the spiral trajectory in the section Disk Experiment.

Coriolis acceleration with radial movement away from the axis of rotation

A person stands on a disk at a distance from the center (red dot A), and further out at a distance $r+\Delta r$ stands a pile (red dot 1). The person throws a body with velocity toward the pole. If the disc were at rest, the body would fly along the red line and $\Delta t=\Delta r/v$ hit the pile after the time Δ If the person is unaware of the rotation (or of its effect on free motion), he will always expect this rectilinear motion in the direction in which he threw the body loose.

While the thrown body is in the air, the disc rotates through angle Δ $\Delta \varphi =\omega \,\Delta t$ , where ω $\omega$ is the angular velocity. The person moving with it covers the distance $r\Delta \varphi$ on its circular arc (blue arrow) and is then located at the red point B. The pile travels a greater distance on its arc $(r+\Delta r)\Delta \varphi$ because it is farther out. He is then at the red point 2. The difference of the two distances of the stake and the person is

$\Delta s=\Delta r\Delta \varphi$ .

The thrower expects the thrown body at the place where the pole is now, i.e. at point 2 at the end of the dotted straight red line. For him, however, the body has flown past the pole along the curved dotted red line at a distance Δ . $\Delta s$

This can be explained from a "stationary" observer, who is standing next to the rotating disc and does not have to take into account any inertial forces caused by the accelerated reference frame: The body initially moved along with the throwing person on the rotating disc. Thus, at the moment of throwing, it has a tangential orbital velocity $v_{t}=\omega \,r$ and receives perpendicular to it the radial throwing velocity addition. After the throw he moves in a straight line (red-blue arrow) with the velocity resulting $v_{t}$ from and In radial direction it covers the distance $v\Delta t$ , in tangential direction the distance $v_{t}\,\Delta t$ and therefore reaches the place marked with the green cross. The distance in the tangential direction is the same as the distance the person travels during its circular arc, because $v_{t}\,\Delta t=r\,\omega \Delta t=r\,\Delta \varphi$ . When the body arrives at the green cross, it still lacks the distance Δ $\Delta s$ to the pole.

Now Δ $\Delta s$ grows quadratically with time, because it holds:

$\Delta s=\Delta \varphi \Delta r=\omega \,\Delta t\,v\,\Delta t=\omega \,v\,(\Delta t)^{2}$ .

For the person rotating along, this looks like a uniformly accelerated movement according to the path-time law

$\Delta s={\frac {1}{2}}\,a\,(\Delta t)^{2}$ ,

where the acceleration.

Thus, the person rotating with the body can detect the deviation of the body from the intended direction by the acceleration

$a_{C}=2\,w\,v$

explain. This is the Coriolis acceleration, which in this case is only tangentially directed.

This derivation is not quite conclusive insofar as the pieces on the circular arcs were treated as straight lines. But this is exact in the limiting case of infinitesimally small distances. Therefore the formula obtained in this way is valid.

Coriolis acceleration for circular motion around the axis of rotation

See also: Centripetal acceleration#Simple derivation

In general, to maintain a circular motion at distance with arbitrary velocity $\tilde v$ requires acceleration ${\tilde {a}}_{\text{r}}={\tilde {v}}^{2}/r$ towards the center. If a rotating body in the inertial frame of reference has velocity ${\tilde {v}}=v$ , then $a_{\text{r}}=v^{2}/r$ results as the centripetal acceleration that occurs in all circular motions and is caused by the centripetal force.

If a body moves with velocity (relative velocity) in a reference frame $\omega$ performing rotational motion with angular velocity ω , then the velocity of the body as seen from the inertial frame is the sum of the orbital velocity $v_{\text{Umlauf}}=\omega \cdot r$ and the relative velocity :

$v=v_{\text{Umlauf}}+v'$ .

For the centripetal acceleration of the body it follows:

$a_{\text{r}}={\frac {(v_{\text{Umlauf}}+v')^{2}}{r}}={\frac {v_{\text{Umlauf}}^{2}}{r}}+{\frac {v{'}^{2}}{r}}+2{\frac {v_{\text{Umlauf}}\,v'}{r}}=a_{\text{Zp}}+a'_{r}+2\,\omega \,v'$ .

This is the centripetal acceleration, which belongs to the considered motion in the resting reference frame. It is composed of three terms. The first is the centripetal acceleration experienced by a body connected to the reference frame. This is followed by the relative acceleration and a term opposite to the Coriolis acceleration. The example shows that this division depends on the chosen reference frame, so it is arbitrary.

Resolved according to the radial acceleration in the rotating reference frame:

$a'_{\text{r}}=a_{\text{r}}-a_{\text{Zp}}-2\,\omega \,v'=a_{\text{r}}+a_{\text{Zf}}+a_{\text{C}}$ .

The second term is the centrifugal acceleration. It is oppositely equal to the centripetal acceleration of a body connected to the reference frame. The third term is the Coriolis acceleration.

No Coriolis acceleration when moving parallel to the axis of rotation

A movement of a body parallel to the axis of rotation does not cause a Coriolis force, because no additional forces are necessary to explain it. For example, consider the case where there is a vertical climbing pole on a horizontal turntable at some distance from the centre, and a person slides down it. For him, the centrifugal force remains constant because the distance from the axis of rotation remains constant. The holding force required to maintain the constant distance, which is applied by the rod, then also remains constant. For an observer at rest, the downward motion parallel to the axis is superimposed on a circular motion about the axis, together this is a screw motion. The centripetal force required for the circular motion about the axis is exerted by the rod and is independent of the height and vertical motion of the body.

At first, it seems to be different if one jumps vertically upwards on the turntable or throws an object upwards parallel to the axis of rotation. When falling down, the starting point is not reached again - neither in relation to the disk nor in relation to the solid ground. But also at this deflection, no Coriolis-force appears, but only temporary missing of holding-force resp. centripetal-force, which at previous example all times was exerted by rod. For the rotating observer, the body is then accelerated outwards by the centrifugal force; for the stationary observer, it simply continues to move in a straight line at its initial instantaneous speed. Both descriptions lead to the same result.

Inadequate derivation

Often (even in some textbooks), the Coriolis force is illustrated or even justified solely by the fact that a body on the rotating disk must obtain a higher circumferential speed with increasing distance from the axis of rotation in order to rotate along with the disk. But this is not a correct reasoning, for it explains only half the magnitude of the Coriolis force, as even a simple calculation using the magnitudes of the vectors shows: If, at a constant radial velocity , the v_r body increases $\Delta t$ its distance by Δ in time $\Delta r=v_{r}\Delta t$ , its tangential velocity increases by Δ . $\Delta v_{t}=\omega \Delta r$ This gives the required acceleration to Δ ${\tfrac {\Delta v_{t}}{\Delta t}}={\tfrac {\omega \Delta r}{\Delta t}}=\omega v_{r}$ . This is only half the real Coriolis acceleration.

The flaw in this insufficient derivation lies in the inconsistent treatment of the velocity of the same object in two reference frames. If a point in space at location is ${\vec {r}}$ moving with velocity in the ${\vec {v}}$ resting reference frame, e.g. along the x-axis, then in the rotating reference frame it is also at location ${\vec {r}}$ (the vector just has different components so that it denotes the same location). But its velocity observed in the rotating reference frame is ${\vec {v}}'$ not equal to ${\vec {v}}$ , but ${\vec {v}}'={\vec {v}}-{\vec {\omega }}\times {\vec {r}}$ , so that it remains on the x-axis, which itself moves (against the direction of rotation) in the rotating reference frame.

For the calculation the rule is decisive, how the time derivative of a variable is to be formed relative to the axes of a rotating reference system. As can be seen in the derivation of this rule, the product rule of the differential calculus is to be applied for the derivation, from which an additional summand results for the time derivative of the moving basis vectors of the rotating coordinate system. Since the acceleration is obtained by differentiating the location twice, the product rule must be applied twice. The error in the above justification of the Coriolis force is that only the first derivation is done correctly, but in the second the motion of the coordinate system is ignored. In formulas the rule for derivation is (where $\bullet$ stands for any vector):

${\frac {\mathrm {d} \bullet }{\mathrm {d} t}}={\frac {\mathrm {d} '\bullet }{\mathrm {d} t}}+{\vec {\omega }}\times \bullet$ .

On the left is how fast the vector $\bullet$ changes in the system at rest, on the right in the first term how this change is perceived in the rotating system.

Substituting for the space $\bullet$ the place ${\vec {r}}(t)\ [={\vec {r}}'(t)]$ gives the formula correctly (because ${\tfrac {\mathrm {d} '{\vec {r}}}{\mathrm {d} t}}={\vec {v}}'$ )

${\vec {v}}={\vec {v}}'+{\vec {\omega }}\times {\vec {r}}'$ .

If one derives this equation as it stands there once again according to time (for constant and ω ${\vec \omega }$ ), without taking into account that the special rule has to be applied again for rotating systems, we obtain for the acceleration (false)

${\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}={\vec {\omega }}\times {\frac {\mathrm {d} {\vec {r}}'}{\mathrm {d} t}}={\vec {\omega }}\times {\vec {v}}'$ .

That's only half the Coriolis acceleration.

Only if you form the derivative of ${\vec {v}}$ correctly so by substituting into the operator equation again ${\vec {v}}$ , you get the additional term with the cross product a second time:

${\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}\,=\,{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\vec {v}}'\,+\,{\vec {\omega }}\times {\vec {r}}'\right)\,=\underbrace {\frac {\mathrm {d} {\vec {v}}'}{\mathrm {d} t}} _{{\vec {a}}\,'+\,{\vec {\omega }}\times {\vec {v}}\,'}\,+\,{\vec {\omega }}\times \underbrace {\left({\frac {\mathrm {d} {\vec {r}}\,'}{\mathrm {d} t}}\right)} _{{\vec {v}}\,'+\,{\vec {\omega }}\times {\vec {r}}\,'}$

(The second summand, after multiplying out, additionally gives also the centrifugal acceleration ω ${\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')$ .)

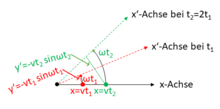
Uniform linear motion along the fixed x-axis, observed from the rotating coordinate system

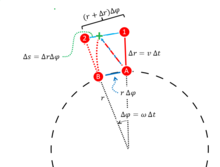
Deflection due to the Coriolis force during radial motion