Coordinate system
![]()
Koordinate is a redirect to this article. A former Lithuanian company was called Koordinatė.
A coordinate system is used to describe points of a set of points in an unambiguous way with the help of numbers, the coordinates. The simplest examples are a number line and Cartesian coordinates in the Euclidean plane. In the first case, a real number is assigned to a point on a straight line. In the second case a point is described by two real numbers. That there are mostly infinitely many possibilities to introduce a coordinate system can be seen in the example of the number line: One has infinitely many possibilities to select a point to which the number 0 is to be assigned. Or in the Euclidean plane: Even after choosing a point as coordinate origin (in short: origin) every (different) pair of number rays through the origin can be chosen as coordinate axes. A point is then 



If other curves, e.g. circles, play an essential role, polar coordinates can be a better choice. In this case only one coordinate can be interpreted as length, the second coordinate describes an angle.
For the description of Euclidean spaces one needs more than two coordinates. One speaks then of a n-tuple (instead of a pair of numbers).
Coordinate domains can also be more general algebraic domains, e.g. complex numbers, solids, skew bodies, ... can occur. A combination of alphabet and natural numbers is used in the description of the squares of a chessboard.
For homogeneous coordinates, one weakens the uniqueness requirement somewhat.
The great advantage of coordinates from an algebraic number range is the then possible solution of geometric problems with the help of algebra (e.g. intersection of a straight line with a circle).
The term coordinate - meaning "indication of position" - was formed in the 18th century from the word ordinate (vertical).
|
| a | b | c | d | e | f | g | h |
|
| 8 |
|
|
|
|
|
|
|
| 8 |
| 7 |
|
|
|
|
|
|
|
| 7 |
| 6 |
|
|
|
|
|
|
|
| 6 |
| 5 |
|
|
|
|
|
|
|
| 5 |
| 4 |
|
|
|
|
|
|
|
| 4 |
| 3 |
|
|
|
|
|
|
|
| 3 |
| 2 |
|
|
|
|
|
|
|
| 2 |
| 1 |
|
|
|
|
|
|
|
| 1 |
|
| a | b | c | d | e | f | g | h |
|
The squares of the chessboard are designated with a pair of numbers and letters.
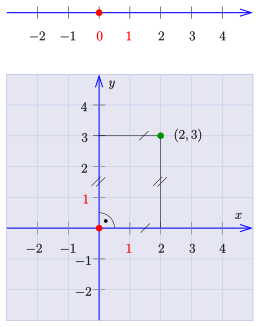
Number line (top), plane Cartesian coordinates (bottom)
Affine coordinate system
→ Main article: Affine coordinates
Selecting three points 



and 


If the vectors 



If the basis vectors are not orthogonal (see picture), we speak of oblique coordinates.
Accordingly, affine coordinates are explained for higher dimensions.
Defining coordinates in this way is possible for any n-dimensional affine space over a body, so is not limited to a Euclidean space.
Since the 3-dimensional space plays an important role in practice, there are certain agreements for the introduction of coordinates, e.g. the legal system.
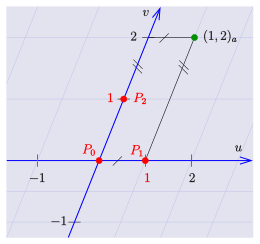
affine coordinates

Left- and right-handed (right) three-dimensional coordinate system
Non-affine coordinate systems
In the plane
Since for calculations of lengths and angles it is advantageous if the curves 

The simplest non-linear orthogonal curve system consists of the rays in a point 


Elliptical coordinates use perpendicularly intersecting systems of confocal ellipses and hyperbolas. These coordinates are not defined for the focal points and the points between them.
In space
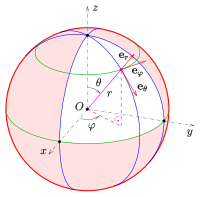
The spatial coordinates corresponding to the polar coordinates are the
Cylinder coordinates. They are defined only for points outside the cylinder axis. and the
Spherical coordinates. Restrictions of the definition ranges and points, to which spherical coordinates are assigned, apply also here.
The (plane) elliptical coordinates correspond to the ellipsoid coordinates. The orthogonal surface system used here consists of confocal ellipsoids, single-shell and double-shell hyperboloids.
Furthermore there are the ellipsoidal coordinates, which are used for the description of points of a rotation ellipsoid (earth).
On surfaces
Parameter representations of surfaces can be seen as coordinate systems of these surfaces. E.g. the parameter representation of a plane, the usual parameter representation of a spherical surface with geographical longitude and latitude or the paramer representation of an ellipsoid.
Other curvilinear coordinate systems
Further examples and applications of coordinate systems can be found in the article curvilinear coordinates.
Local coordinate systems
If are 



In polar coordinates, one vector points in the direction of the radius and the other in the direction of the tangent of the circle through 
In space, one determines the tangent vectors to the curves passing through a point 


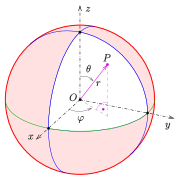
Spherical coordinates
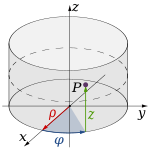
Cylinder coordinates
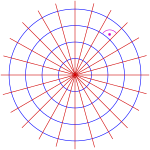
Polar coordinates
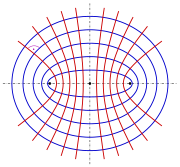
elliptic coord.
Search within the encyclopedia