Control system

A control loop is the dynamic action sequence between controller and controlled system for influencing the controlled variable y(t) in a closed system, in which this variable is continuously measured and compared with the reference variable . w(t)

An important factor here is the negative feedback of the current value of the controlled variable to the controller e(t)=w(t)-y(t) which continuously counteracts a deviation from the reference variable. A constant reference variable is referred to as a set point.

It is the task of the controller to determine the time response of the controlled variable with regard to its dynamic behavior according to specified requirements. More complex control loop structures may be required to meet conflicting requirements such as good command and disturbance behavior.

For the design of a control loop with a controller, the mathematical model of the controlled system is required. For limited, nonlinear and dead-time systems, the use of numerical calculation is recommended. The classical graphical controller design methods (Bode diagram, locus of frequency response, root locus method) have only a didactic informative meaning.

A stable control loop can become unstable when parameters are changed, even if the individual components of the control loop are stable in themselves. On the other hand, a control loop with an optimized controller can also behave stably if a single control loop element is unstable.

Control loops can be found in many fields besides engineering: Biology, ecology, economics, quality management, corporate structures, linguistics and others.

$\to$ See also main article Control engineering, article Controller, article Controlled system.

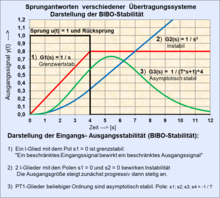
Example of the representation of stability for different dynamic systems

Control loops outside the technology

Biological control circuits

The term "control loop" is used in biology to describe processes in living organisms for the maintenance of homeostasis. Control loops are therefore not always purely technical models, but a general organisational principle that can also be understood under terms such as self-regulation and systems theory. There are both relatively simple and more complex ones at the physiological level within the organ systems of higher organisms that contribute to their homeostasis through negative feedback, up to the highly complex control loops within communities at the level of ecology. Examples:

End product inhibition of enzyme activity in cells and tissues.
Regulation of the water balance in plants
Regulation of respiration (a humoral control circuit based on chemoreceptors)
Regulation of the oxygen content of the blood
Thermoregulation: Animals at the same temperature require a certain body temperature for survival, which varies within a tolerance band, but should not leave this band. The nervous system of every animal of the same temperature therefore contains a temperature control circuit with corresponding receptors as sensors, and blood vessels that can dilate and constrict, as well as muscles as regulators, in humans also variable transpiration.
Regulation of the water balance and the acid-base balance by the kidney
Pulse regulation: For the adequate supply of the cells with oxygen and energy, sufficient blood circulation is required, which depends on the physical load. This is ensured, among other things, by the regulation of the heart rate and the cardiac output by the autonomic nervous system.
Blood pressure regulation: If the blood pressure is too low, sufficient blood circulation and supply of the cells with oxygen and energy is not possible. Too high blood pressure damages the organs. Therefore, there is a blood pressure regulation in animals and humans.
Regulation of the amount of light entering the eye by enlarging or reducing the pupil and the adaptation of other sensory organs (Weber-Fechner law).
Regulation of the blood level of numerous hormones (e.g. in the thyrotropic control circuit)
Regulation of food intake through hunger and satiety
Regulation of the blood sugar level: The blood sugar ensures the energy supply of the organism and is adapted to the physical strain.
Regulation of population density through predator-prey relationships
There is also a control loop in species protection; the target value here is the favourable conservation status of populations.

Economic control loops

From the field of economics, the following should be mentioned:

market pricing
Market regulation of the state.
spider web theorem, pig cycle

Management-oriented control loops

management cycle
Control loop of personnel management

Quality Circle

In the area of quality management, there is the quality circle, on which quality management systems are based in accordance with the DIN EN ISO 9001:2015 regulations.

Linguistic control circuits

In the article Linguistic Synergetics it is shown that Quantitative Linguistics has developed control circuits on different language levels (morphology(linguistics), writing, syntax and others), which partly also act beyond the language levels or connect them with each other.

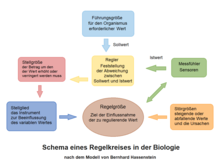
Scheme of a control loop according to Bernhard Hassenstein

Control loops in technology

Introduction

A real control loop consists of several individual components of the controlled system and the controller, each of which has a specific time response. While the controlled system is usually available as a technical system, a system analysis of the controlled system is required for the mathematical treatment of the closed loop, from which a mathematical model can be determined. The model should largely correspond to the time response of the real controlled system. The observation of a signal course at a transmission system for a given input signal u(t) starts at $t_{0}=0$ and ends for the course of the output signal y(t) with $t>t_{0}$ .

In conjunction with the controlled system model $G_{S}(s)$ , a controller $G_{R}(s)$ be parameterized, which ensures stability for the closed loop according to the closing condition $G(s)={\tfrac {G_{R}\cdot G_{S}}{1+G_{R}\cdot G_{S}}}$ . In general, the parameters of the controller cannot be adjusted optimally by hand for more complicated controlled systems. Industrial control processes with controller mismatches can cause destruction of equipment due to amplitude build-up of the controlled variable.

Modern electronics allow the realization of arbitrarily complex controller structures with justifiable economic expenditure. In many cases, digital controllers are used instead of analog controllers and may be combined with digital measuring and control elements. The digital signals are value and time discrete signals. These control loops behave like analog control loops if the resolution and sampling rate are high enough.

For the design of a controller in engineering, the mathematical model of the controlled system is required. For multivariable systems (MIMO) the controller design with the state space representation is suitable, for nonlinear and dead-time single-variable systems (SISO) the numerical calculation is recommended. The classical graphical controller design methods (Bode diagram, locus of frequency response, root locus method) have only didactic informative significance.

The most common mathematical system descriptions are the differential equation f(t) , the transfer function G(s) , the frequency response $H(j\omega )$ and the discrete-time difference equation $y(k)=y(k-1)+f\,[u(k),\,System]$ .

The aim of the mathematical descriptions of control loop elements is the calculation of the dynamic input and output behaviour of individual components, closed control loops and their stability.

Due to required quality criteria (control quality) of the transient process of the controlled variable, the heuristic method "trial and error" is usually used in the offline simulation of the control loop.

Simulation of the input and output behaviour of a control loop

Unfortunately, individual components of most technical controlled systems behave non-linearly. The transfer function and its algebraic calculation may only be used for linear transfer systems.

If, for example, the controlled system contains a dead time (transport time), limiting effects of some components or other non-linearities, the discrete-time calculation of the control loop with difference equations is practically the only option for the system calculation. The open control loop is closed by the relation ${\text{Sollwert - Istwert}}:\,w(k)=e(k)-y(k)$ as input variable of the controller, which determines the desired behavior of the control loop with its time response.

Difference equations or a chain of difference equations describing several elementary systems connected in series let the output quantity $u_{(k)}$ calculated $y_{(k)}$ algebraically for a small time step Δ $\Delta t$ depending on the input signal The numerical overall solution of the system is - in the case of simple difference equations - done recursively over many computational sequences, each in small constant time intervals. The form of the overall solution is thus tabular.

The typical form of a recursive difference equation of common control loop elements (linear factors) is:

$y(k)=y(k-1)\,+f\,[u(k),\,\Delta t,\,T]$ .

Where $u_{(k)}\,{\text{die Eingangsgröße}},\,\Delta {t}\,\,{\text{ein kleines Zeitintervall}}\,{\text{und T = die Systemzeitkonstante}}$ . The sequence $k=(0,1,2,3,\dots ,k_{\mathrm {max} })$ describes a finite number of the sequence members.

Difference equations of the linear time-dependent system components can be derived from ordinary differential equations by replacing the differential quotients by difference quotients Δ . ${\tfrac {\Delta y}{\Delta t}}$ Nonlinear transfer systems can be described, for example, by logical statements such as IF-THEN-ELSE statements or tables.

$\to$ See article difference equation.

Digital controllers

Digital control means that the input signal of a dynamic system or a subsystem is sampled at specific discrete points in time, calculated synchronously in time and output as a digital output signal. Other terms refer to this process as "discrete-time control" or also as "sampling control".

Digital controllers are implemented by microcomputers. They process difference equations suitable for the desired control behavior of the overall system.

Since the controlled systems are mostly given analog systems, the interface of the system requires an analog input signal via a DA converter.

Advantages: One-time hardware development effort, easy parametric system changes via software, realization of more complex controller structures, multitasking.

Disadvantages: The use of a digital controller is only worthwhile for larger production quantities due to the increased technical effort.

$\to$ See article Digital controller, Z-transform and difference equation.

Block diagram of a simple standard control loop consisting of the controlled system, the controller and a negative feedback of the controlled variable y (also actual value). The controlled variable y is compared to the reference variable (set point) w. The system deviation e = w - y is fed to the controller, which uses it to form a manipulated variable u according to the desired dynamics of the control loop. The disturbance variable d usually affects the output of the controlled system, but it can also influence different parts of the controlled system.