Continuous function

In mathematics, a continuous mapping or continuous function is a function in which sufficiently small changes in the argument result in only arbitrarily small changes in the function value. One can formalize this property with the interchangeability of the function with limit values or with the ε $\varepsilon$ - $\delta$ criterion.

In visual terms, a real continuous function y=f(x) is characterized by the fact that its graph in a Cartesian coordinate system is a continuous curve within its domain of definition, i.e. the graph does not make any jumps and can be drawn without setting down the pencil.

Many functions used in the practice of real analysis are continuous, in particular this is the case for all differentiable functions.

For continuous functions a number of useful properties can be proved. Examples are the intermediate value theorem, the theorem of minimum and maximum and the fundamental theorem of calculus.

More generally, the concept of continuity of mappings is central to mathematics, especially in the subfields of analysis and topology. It is possible to characterize continuity by a condition that uses only terms of topology. Thus the notion of continuity can be extended to functions between topological spaces. This general view turns out to be the most "natural" approach to the notion of continuity from a mathematical point of view: continuous functions are those functions between topological spaces which are "compatible" with their structures. Thus, continuous functions play a similar role in topology and analysis as homomorphisms do in algebra.

Motivation

The function

$f(x)={\begin{cases}x,&{\text{wenn }}x\leq 1\\x+1,&{\text{wenn }}x>1\end{cases}}$

"jumps" at the point x=1 from the function value 1 to the function value 2. If the function represents a connection from nature or technology, such behavior appears unexpected (Natura non facit saltus). If, for example, the function describes the relationship between the energy expended in cycling and the speed achieved, it would be surprising if a minimal increase in the energy expended at one point led to a sudden doubling of the speed.

The mathematical notion of continuity attempts to accurately describe those functions that do not have such "arbitrary" behavior. Thus, the given function is not continuous, where the discontinuity can be restricted to the point . x=1 In all other points the function is continuous.

Continuity is often associated with being able to draw the graph of a function in one go, without having to drop it. This view reaches certain limits, especially when considering functions with other ranges of definition than the entire real number line. Therefore mathematically exact definitions are needed.

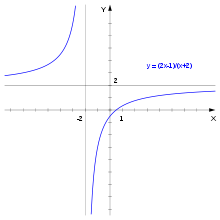
For example, the

$g(x)={\begin{cases}x\cdot \sin {\frac {1}{x}},&{\text{wenn }}x\not =0\\0,&{\text{wenn }}x=0\end{cases}}$

given function is clearly continuous, because except at x=0 its graph is a continuous line, and at x=0 it has no place to make "jumps". But whether it can be "drawn without settling" to the zero point cannot be decided without a more precise definition of what an allowed drawing should be. There it is easier to develop a definition of "steady" without the notion of "drawing", according to which this function can be proved to be steady. Then the reasons just mentioned may well contribute to the proof.

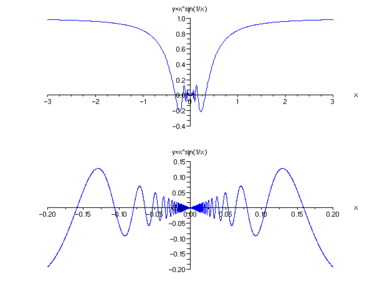
Detailed study of the behavior of g(x) near the point x=0 : Drawing possible?

The function is even, so it suffices to restrict the investigation to its behavior for $x\geqq 0$ Besides the zero at the zero point, its positive zeros are at the points $x_{k}={\tfrac {1}{k\pi }}$ for integer k>0 ; these are indexed from right to left, i.e. $x_{1}>x_{2}>\dotsb >0$ with $x_{1}$ as the largest zero and with each infinitely many other zeros between $0$ and any other zero $x_{k}$ . Between the adjacent zeros $x_{k}$ and $x_{k-1}$ lies one place ξ $\xi _{k}={\tfrac {2}{(2k-1)\cdot \pi }}$ with , $\sin {\tfrac {1}{\xi _{k}}}=\pm 1$ such that $|g(\xi _{k})|=\xi _{k}={\tfrac {2}{(2k-1)\cdot \pi }}>{\tfrac {1}{k\pi }}$ . Thus, between the zeros $x_{k}$ and the graph must $x_{k-1}$ twice ${\tfrac {1}{k\pi }}$ overcome the height difference its length in this section is more than ${\tfrac {2}{k\pi }}$ Between the zero $x_{1}$ and any other positive zero $x_{n}$ further left, the length of the graph is thus greater than ${\tfrac {2}{\pi }}\cdot ({\tfrac {1}{1}}+{\tfrac {1}{2}}+\dotsb +{\tfrac {1}{n-1}})$ . This sum grows as increases across all bounds (see Harmonic Series), so the complete drawing would never be finished.

Graphical illustration of the function with a jump point in x=1 .

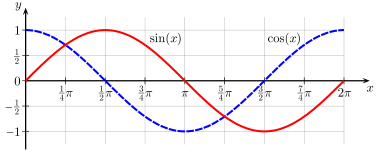
Sine and cosine are continuous functions, their function graphs can be drawn in one go without stopping.

The graph of the continuous function $x\sin(1/x)$ in two different scales.

Continuity of real functions

Definition

Let be a real function, that is, a function $f\colon D_{f}\to \mathbb {R}$ , whose function values are real numbers and whose domain of definition $D_{f}\subset \mathbb {R}$ also consists of real numbers.
In real analysis, there are several equivalent ways to define the continuity of in an ${\displaystyle x_{0}\in D_{f}}$ . The most common are the epsilon delta criterion and the definition using limits.

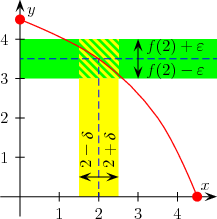
Definition by epsilon delta criterion. is called continuous in $x_{0}$ if for every ε $\delta >0$ there exists $\varepsilon >0$ a δ such that for all $x\in D_{f}$ with

$|x - x_0| < \delta$

applies:

$|f(x) - f(x_0)| < \varepsilon$ .

Intuitively, the continuity condition means that for every change ε $\varepsilon$ in the function value that one is willing to accept, one can find a maximum change δ $\delta$ in the argument that ensures this default.

Example: Prove continuity of the function $f(x)=2x+3$ at the point $x_{0}$

Let $x,x_{0}\in \mathbb {R}$ and ε $\varepsilon \in \mathbb {R}$ with

$\varepsilon >0$ .

It's

$|f(x)-f(x_{0})|=|(2x+3)-(2x_{0}+3)|=|2x-2x_{0}|=2|x-x_{0}|$ .

To make this smaller than the given number ε $\varepsilon$ , for example.

$\delta (\varepsilon )={\tfrac {1}{2}}\varepsilon$

be chosen. Because from

$|x-x_{0}|<\delta ={\tfrac {1}{2}}\varepsilon$

then follows namely

$|f(x)-f(x_{0})|=2|x-x_{0}|<2\cdot {\tfrac {1}{2}}\varepsilon =\varepsilon$ .

Comments:

Since the function at every point $x_{0}\in \mathbb {R}$ is continuous, is thus continuous on all of $\mathbb {R}$ continuous.
Because δ $\delta$ can only be derived from ε $\varepsilon$ , but not from the location $x_{0}\in \mathbb {R}$ is even continuous on all of $\mathbb {R}$ uniformly continuous.

Definition by means of limit values. With this definition one demands the interchangeability of function execution and limit value formation. Here one can either rely on the notion of limits for functions or for sequences.
In the first case one formulates: is called continuous in $x_{0}$ if the limit $\lim _{x\to x_{0}}f(x)$ exists and $f(x_{0})$ coincides with the function value i.e. if holds:

$\lim _{x\to x_{0}}f(x)=f(x_{0})$ .

In the second case, one formulates: is said to be continuous in $x_{0}$ for every sequence $x_{0}$ convergent to $(a_{n})$ with elements $a_{n}\in D_{f}$ , the sequence ${\bigl (}f(a_{n}){\bigr )}$ $f(x_{0})$ converges to
The second condition is also called the sequence criterion.

Instead of continuity in $x_{0}$ one often speaks of continuity in the point $x_{0}$ or continuity in the place $x_{0}$ . If this condition is not satisfied, then called discontinuous in (at the point/place) $x_{0}$ , or denote $x_{0}$ as the discontinuity point of .

A function is said to be continuous if it is continuous at every point in its domain.

Examples of continuous and discontinuous functions

If a function is differentiable at one point, it is also continuous there. Thus follows in particular the continuity

of all rational functions (so, for example, $x\mapsto x^{3}+4x^{2}-6x+9$ or $x\mapsto {\frac {2x-1}{x+2}}$ )
of the exponential functions $x \mapsto a^x$ , for fixed $a\in \mathbb {R} ^{>0}$
the trigonometric functions (i.e. sine, cosine, tangent,...)
of the logarithm functions

But the continuity of these functions can be proved directly without recourse to the notion of differentiability.

The absolute value function is also continuous, even if it is not differentiable at the point 0. Also continuous are all power functions (for example $x\mapsto x^{\frac {1}{2}}={\sqrt {x}}$ ), although they are also not differentiable for an exponent less than 1 at the point 0.
In fact, all elementary functions are continuous (for example, $x\mapsto {\sqrt {1+\cos ^{2}(x-5)}}$ ).

When considering elementary functions, however, it should be noted that some elementary functions have as their domain of definition only a real subset of the real numbers. For example, the square root function omits all negative numbers, and the tangent function omits all zeros of the cosine.
In these cases, it is sometimes imprecisely formulated that the functions are discontinuous in the corresponding places. However, this is not correct, since the question of continuity only arises for points in the domain of definition. Mathematically meaningful, however, is the question of a continuous continuation of the function at a definition gap.
For example, the function

$x\mapsto {\frac {2x-1}{x+2}}$

defined for all real numbers $x\not =-2$ and continuous in every point of its domain. It is therefore a continuous function. The question of continuity in does x=-2 not arise because this point is not part of the domain of definition. A continuous continuation of the function at this definition gap is not possible.

The absolute value function and the root function are examples of continuous functions that are not differentiable at individual points in the domain of definition. At the beginning of the 19th century, mathematical experts still assumed that a continuous function must be differentiable at least at "most" places. Bernard Bolzano was then the first mathematician to construct a function that is continuous everywhere but differentiable nowhere, the Bolzano function. However, he did not publish his result. In the 1860s, Karl Weierstrass also found such a function, known as the Weierstrass function, which caused a sensation in the mathematical world. The graph of the Weierstrass function can effectively not be drawn. This shows that the intuitive explanation that a continuous function is one whose graph can be drawn without setting down the pencil can be misleading. Ultimately, one must always resort to the exact definition when investigating the properties of continuous functions.

Using methods of 20th century mathematics, it could even be shown that the functions which are nowhere differentiable are in a sense "frequent" among the continuous functions.

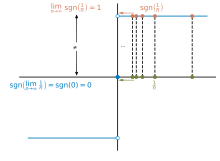
Simple examples of discontinuous functions are:

the sign function (discontinuous only in 0)
the Dirichlet function (discontinuous at every point)
the Thomaean function (discontinuous exact in all rational numbers).

Continuity of composite functions

Similar to differentiability, continuity is a property that transfers from the components to the functions composed of them in many operations. For the following points, let the continuity of in $x_{0}$ already be given.

Consecutive execution: if is another real function whose domain of definition spans the range of values of and is $f(x_{0})$ continuous in then the composition is $g\circ f$ continuous in $x_{0}$ .
Algebraic operations: If is another real function with the same domain of definition as , which is also continuous in $x_{0}$ , then the pointwise defined functions , $f-g$ , $f \cdot g$ and $\tfrac{f}{g}$ also continuous in $x_{0}$ . In the latter case, however, note that the domain of definition of the composite function turns out to be $D_{f}$ without the zero set of . In particular, $x_{0}$ may thus not be a zero of even in this case.
Maximum/minimum: Under the same conditions as in the previous point, the pointwise defined functions $\max(f,g)$ and are $\min(f,g)$ continuous in $x_{0}$ .

If the definition ranges of the functions involved do not match as required, you may be able to help yourself by placing suitable restrictions on the definition ranges.

Under certain conditions continuity also transfers to the inverse function. However, the statement cannot be formulated here for point-wise continuity:

If the domain of the injective continuous real function an interval, then the function is strictly monotone (increasing or decreasing). The inverse function defined on the range of values of $f^{-1}$ is also continuous.

Using these permanence properties, one can derive, for example, the continuity of the elementary function given above $x\mapsto {\sqrt {1+\cos ^{2}(x-5)}}$ from the continuity of the cosine, the identical function, and the constant functions. Generalizing this reasoning, the continuity of all elementary functions follows as a consequence of the simple examples given earlier.

Main theorems about continuous real functions

There are a number of important theorems that hold for continuous real-valued functions These are most easily formulated by assuming that $D_{f}=[a,b]$ with $a,b\in \mathbb {R} ,a<b$ is a closed bounded interval:

Intermediate value set: the function takes any value between and .

Theorem of Minimum and Maximum: is bounded and infimum and supremum of its function values are also assumed to be function values. So it is really a matter of minimum and maximum. This theorem proved by Weierstrass, sometimes called the extreme value theorem, only provides the existence of these extreme values. For their practical finding, statements from the differential calculus are often necessary.

Fundamental theorem of analysis: is Riemann integrable and the integral function

$F(x)=\int _{a}^{x}f(t)\,{\rm {d}}t$

is a primitive function of .

Heine's theorem: satisfies a stricter version of the epsilon-delta criterion. The corresponding property is called uniform continuity.

From the intermediate value theorem and the theorem of minimum and maximum together it follows that the image of is also a closed, bounded interval (or, in the case of a constant function, a single-point set).

Other continuity terms

Tightening of the concept of continuity are, for example, uniform continuity, (local) Lipschitz continuity, Hölder continuity as well as absolute continuity and geometric continuity. Ordinary continuity is sometimes called pointwise continuity to distinguish it from uniform continuity. Applications of Lipschitz continuity can be found, for example, in existence and uniqueness theorems (e.g., Picard-Lindelöf's theorem) for initial value problems of ordinary differential equations and in geometric measure theory. Absolute continuity is used in stochastics and measure theory, geometric continuity in geometric modeling.

One property that a set of functions may possess is uniform continuity. It plays a role in the frequently used theorem of Arzelà-Ascoli.

The sign function $\sgn(x)$ is not continuous at position 0.

The graph of a continuous rational function. The function is not defined for x=-2 .

Illustration of the ε $\varepsilon$ - $\delta$ -definition: for ε , δ $\varepsilon =0.5$ satisfies $\delta =0.5$ the continuity condition.

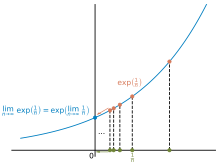
Example for the sequence criterion: The sequence exp(1/n) converges to exp(0)