Confidence interval

A confidence interval, or CI, (also called confidence interval, confidence interval, or expected range) is, in statistics, an interval intended to indicate the precision of the lag estimate of a parameter (e.g., a mean). The confidence interval indicates the range that includes with a certain probability (the confidence level) the parameter of a distribution of a random variable.

If a random experiment is repeated many times in an identical manner, the frequently chosen 95% confidence interval will contain the fixed, unknown, "true" parameter 95% of the time.

The frequently encountered formulation that the true value lies with 95 % probability in the currently available confidence interval is, strictly speaking, incorrect, since the true value is fixed and does not behave stochastically. The correct formulation would be: the true value lies for 95 % of all samples in the respective calculated confidence interval, because the upper and lower limits of the confidence interval depend on the present sample and are therefore random variables, i.e. stochastic. An alternative correct formulation is: when calculating a confidence interval, its interval boundaries enclose the true parameter 95% of the time and not 5% of the time. The confidence interval is constructed such that the true parameter β is \beta_j1-\alpha covered with probability when the estimation procedure is repeated for many samples, where α \alpha the so-called level of error.

Estimating parameters using confidence intervals is called interval estimation, and the corresponding estimator is called a range or interval estimator. One advantage over point estimators is that a confidence interval can be used to read significance directly: a wide interval for a given confidence level indicates a small sample size or strong variability in the population.

Confidence intervals are distinguished from forecast intervals and confidence and forecast bands.

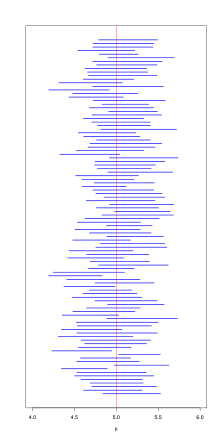
Confidence intervals at the 95% level for 100 samples of size 30 from a normally distributed population. Of these, 94 intervals cover the exact expected value μ = 5; the remaining 6 do not.Zoom
Confidence intervals at the 95% level for 100 samples of size 30 from a normally distributed population. Of these, 94 intervals cover the exact expected value μ = 5; the remaining 6 do not.

Definition

For a fixed given γ\gamma \in (0,1), a γ {\displaystyle \gamma \cdot 100\,\%}-confidence interval for \vartheta to the confidence level γ \gamma (also: a γ \gamma -confidence interval) by the two - based on a random sample {\displaystyle X_{1:n}}- based on a random sample {\displaystyle T_{u}=h_{u}(X_{1:n})}and {\displaystyle T_{v}=h_{v}(X_{1:n})}which are

{\displaystyle P\left(T_{u}\leq \vartheta \leq T_{v}\right)=\gamma \quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta }

satisfy. The statistics {\displaystyle T_{u}}and {\displaystyle T_{v}} are the bounds of the confidence interval, for which always {\displaystyle T_{u}<T_{v}}assumed. The confidence level γ \gamma is also called the coverage probability. The realizations {\displaystyle t_{u}}and {\displaystyle t_{v}} of and {\displaystyle T_{u}}respectively, {\displaystyle T_{v}}form the estimation interval {\displaystyle [t_{u},t_{v}]}. The bounds of the confidence interval are functions of the random sample {\displaystyle X_{1:n}}and therefore also random. In contrast, the unknown parameter is \vartheta fixed. Repeating the random experiment in an identical way, a γ -confidence interval{\displaystyle \gamma \cdot 100\,\%} will cover the unknown parameter \vartheta in γ {\displaystyle \gamma \cdot 100\,\%}all cases. However, since the unknown parameter \vartheta is not a random variable, one cannot say that \vartheta \gamma lies in a γ {\displaystyle \gamma \cdot 100\,\%}-confidence interval with probability γ Such an interpretation is reserved for the Bayesian counterpart of confidence interval, called credibility intervals. The confidence level γ \gamma is also called the coverage probability. Often one sets γ {\displaystyle \gamma =1-\alpha }. The probability 1-\alpha can be interpreted as a relative frequency: If one uses intervals for a large number of confidence estimates, each of which 1-\alpha has the level the relative frequency with which the concrete intervals cover the parameter approaches the value 1-\alpha .

Formal definition

General conditions

Given a statistical model (X,{\mathcal A},(P_{\vartheta })_{{\vartheta \in \Theta }})and a function

{\displaystyle g\colon \Theta \to \Gamma },

which is also called parameter function in the parametric case. The set Γ \Gamma contains the values that can be the result of an estimation. Usually, Γ {\displaystyle \Gamma \subset \mathbb {R} ^{n}}

Confidence interval

An illustration

{\displaystyle C\colon X\to {\mathcal {P}}(\Gamma )}

is called a confidence interval, confidence region, range estimator, or range estimator if it satisfies the following condition:

  • For all γ{\displaystyle \gamma \in \Gamma }, the set {\displaystyle A(\gamma ):=\{x\in X\mid \gamma \in C(x)\}} \mathcal A contained in (M)

Thus, a confidence region is a mapping that assigns to each observation \Gamma an x\in Xinitially arbitrary subset of Γ ( {\displaystyle {\mathcal {P}}(\Gamma )}is here the power set of the set Γ \Gamma , that is, the set of all subsets of Γ \Gamma )

Condition (M) ensures that all sets can be assigned {\displaystyle A(\gamma )}a probability. This is needed to define the confidence level.

Confidence interval

If Γ {\displaystyle \Gamma \subset \mathbb {R} }and if {\displaystyle C(x)}x\in Xalways an interval for any , then Calso called a confidence interval.

If confidence intervals are defined in the form

{\displaystyle C_{1}(x)=(-\infty ,b^{+}(x)],\;C_{2}(x)=[b^{-}(x),b^{+}(x)]\;\;{\text{oder}}\;\;C_{3}(x)=[b^{-}(x),+\infty )},

is defined, then {\displaystyle b^{+}(x)}also called the upper confidence bound and {\displaystyle b^{-}(x)}the lower confidence bound.

Confidence level and level of error

Given a confidence region C. Then C is called a confidence region at the confidence level or certainty level {\displaystyle 1-\alpha }if

{\displaystyle P_{\vartheta }(\{x\in X\mid g(\vartheta )\in C(x)\})\geq 1-\alpha \quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta }.

The value α \alpha is then also called the level of error. A more general formulation is possible with shape hypotheses (see Shape Hypotheses#Confidence Ranges for Shape Hypotheses).

For the above-mentioned special cases with confidence intervals with upper and lower confidence limits, the following is thus obtained

{\displaystyle P_{\vartheta }(g(\vartheta )\leq b^{+}(x))\geq 1-\alpha }

respectively

{\displaystyle P_{\vartheta }(b^{-}(x)\leq g(\vartheta )\leq b^{+}(x))\geq 1-\alpha }

and

{\displaystyle P_{\vartheta }(b^{-}(x)\leq g(\vartheta ))\geq 1-\alpha \quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta .}

Questions and Answers

Q: What is a confidence interval in statistics?


A: A confidence interval is a special interval used to estimate a parameter, such as the population mean, giving a range of acceptable values for the parameter instead of a single value.

Q: Why is a confidence interval used instead of a single value?


A: A confidence interval is used instead of a single value to account for the uncertainty of estimating a parameter based on a sample, and to give a likelihood that the real value of the parameter is within the interval.

Q: What is a confidence level?


A: A confidence level is the likelihood that the parameter being estimated is within the confidence interval, and is often given as a percentage (e.g. 95% confidence interval).

Q: What are confidence limits?


A: Confidence limits are the end points of a confidence interval, which define the range of acceptable values for the parameter being estimated.

Q: How does the confidence level affect the confidence interval?


A: In a given estimation procedure, the higher the confidence level, the wider the confidence interval will be.

Q: What assumptions are required to calculate a confidence interval?


A: The calculation of a confidence interval generally requires assumptions about the nature of the estimation process, such as the assumption that the distribution of the population from which the sample came is normal.

Q: Are confidence intervals robust statistics?


A: Confidence intervals, as discussed below, are not robust statistics, though adjustments can be made to add robustness.

AlegsaOnline.com - 2020 / 2023 - License CC3