Complex number

The complex numbers extend the number range of the real numbers in such a way that the equation x^2 + 1 = 0 becomes solvable. Since the body of real numbers is an ordered body and thus all real square numbers are non-negative, the solution of this equation cannot be real. So a new number is needed, it is $\mathrm {i}$ called , with the property $\mathrm {i} ^{2}=-1.$ This number $\mathrm {i}$ is called an imaginary unit. In electrical engineering, the letter $\mathrm {j}$ used instead to avoid confusion with a current intensity (denoted by or i(t) ) dependent on time

Complex numbers can be $a+b\cdot \mathrm i$ represented in the form where and are real numbers and $\mathrm {i}$ the imaginary unit. The usual calculation rules for real numbers can be applied to the complex numbers represented in this way, whereby $\mathrm i^2$ always be replaced by and vice versa. For the set of complex numbers, the symbol $\mathbb {C}$ (Unicode U+2102: ℂ, see letter with double bar) is used.

The number range of the complex numbers constructed in this way forms an extension body of the real numbers and has a number of advantageous properties that have proved extremely useful in many areas of natural science and engineering. One of the reasons for these positive properties is the algebraic closure of the complex numbers. This means that every algebraic equation of positive degree over the complex numbers has a solution, which is not true for real numbers. This property is the content of the fundamental theorem of algebra. Another reason is a connection between trigonometric functions and the exponential function (Euler formula), which can be established via the complex numbers. Furthermore, every function that can be differentiated once in a complex way on an open set can also be differentiated there as often as desired - unlike in the analysis of the real numbers. The properties of functions with complex arguments are the subject of function theory, also called complex analysis.

The complex numbers (ℂ) include the real numbers (ℝ) , which include the rational numbers (ℚ), which in turn include the integers (ℤ) and the natural numbers (ℕ)

The letter C with double bar stands for the set of complex numbers

Definition

The complex numbers can be defined as a number range in the sense of a set of numbers for which the basic arithmetic operations of addition, multiplication, subtraction and division are explained, with the following properties:

The real numbers are contained in the complex numbers. This means that every real number is a complex number.
The associative law and the commutative law apply to the addition and multiplication of complex numbers.
The distributive law applies.
For each complex number there exists a complex number such that .
For each non-zero complex number there exists a complex number $\tfrac{1}{x}$ such that $x\cdot {\tfrac {1}{x}}=1$ .
There exists a complex number $\mathrm {i}$ with property $\mathrm i^2=-1$ .
Among all number ranges with the previously mentioned properties, the complex numbers are minimal.

The last requirement is equivalent to saying that any complex number can be expressed in the form $a+b\cdot\mathrm i$ (or in shortened notation $a+b\,\mathrm i$ or also $a+\mathrm {i} \,b$ ) can be represented with real numbers and The imaginary unit $\mathrm {i}$ is not a real number. The existence of such a number range is proven in the section on the construction of the complex numbers.

Using the notions of bodies and isomorphism, this can be formulated as follows: There are minimal bodies containing the body of real numbers and an element $\mathrm {i}$ with property $\mathrm i^2=-1$ In such a body, each element has one and only one representation as $z=a+b\,\mathrm {i}$ with real a, b. The complex numbers are isomorphic to any such body.

The coefficients a,b $a + b\,\mathrm i$ called the real or imaginary part of Two notations have become established for this:

$a=\operatorname {Re} {(a+b\,\mathrm {i} )}$ and $b=\operatorname {Im} {(a+b\,\mathrm {i} )}$
$a=\Re {(a+b\,\mathrm {i} )}$ and $b=\Im {(a+b\,\mathrm {i} )}$

Calculating in the algebraic form

Addition

For the addition of two complex numbers $z_{1}=a+b\,\mathrm {i}$ with $a,b\in \mathbb {R}$ and $z_{2}=c+d\,\mathrm {i}$ with $c,d\in {\mathbb {R}}$ holds

$z_{1}+z_{2}=(a+c)+(b+d)\,\mathrm {i} .$

Subtraction

For the subtraction of two complex numbers $z_{1}$ and $z_{2}$ (see addition) applies

$z_{1}-z_{2}=(a-c)+(b-d)\,\mathrm {i} .$

Multiplication

For the multiplication of two complex numbers $z_{1}$ and $z_{2}$ (see addition) applies

$z_{1}\cdot z_{2}=(ac+bd\,\mathrm {i} ^{2})+(ad+bc)\,\mathrm {i} =(ac-bd)+(ad+bc)\,\mathrm {i} .$

Division

For the division of the complex number $z_{1}$ by the complex number $z_{2}$ (see addition) with $z_{2}\neq 0$ one expands the fraction with the complex number $z_{2}$ conjugated to the denominator z ${\bar {z}}_{2}=c-d\,\mathrm {i}$ . The denominator thus becomes real and positive (and is just the square of the amount of $c+d\,\mathrm i$ ):

${\frac {z_{1}}{z_{2}}}={\frac {(a+b\,\mathrm {i} )(c-d\,\mathrm {i} )}{(c+d\,\mathrm {i} )(c-d\,\mathrm {i} )}}={\frac {ac+bd}{c^{2}+d^{2}}}+{\frac {bc-ad}{c^{2}+d^{2}}}\mathrm {i} .$

Calculation examples

Addition:

$(3+2\mathrm {i} )+(5+5\mathrm {i} )=(3+5)+(2+5)\mathrm {i} =8+7\mathrm {i}$

Subtraction:

$(5+5\mathrm i) - (3+2\mathrm i) = (5-3) + (5-2)\mathrm i = 2 + 3\mathrm i$

Multiplication:

$(3+5\mathrm {i} )\cdot (4+11\mathrm {i} )=(3\cdot 4-5\cdot 11)+(3\cdot 11+5\cdot 4)\mathrm {i} =-43+53\mathrm {i}$

Division:

${{\frac {(2+5{\mathrm {i}})}{(3+7{\mathrm {i}})}}={\frac {(2+5{\mathrm {i}})}{(3+7{\mathrm {i}})}}\cdot {\frac {(3-7{\mathrm {i}})}{(3-7{\mathrm {i}})}}={\frac {(6+35)+(15{\mathrm {i}}-14{\mathrm {i}})}{(9+49)+(21{\mathrm {i}}-21{\mathrm {i}})}}={\frac {41+{\mathrm {i}}}{58}}={\frac {41}{58}}+{\frac {1}{58}}\cdot {\mathrm {i}}}$

The addition of two complex numbers in the complex plane illustrates

Other properties

The body $\mathbb {C}$ the complex numbers is on the one hand an upper body of $\mathbb {R}$ on the other hand a two-dimensional -vector space $\mathbb {R}$ . The isomorphism $\mathbb {C} \cong \mathbb {R} ^{2}$ also called natural identification. Usually, one also uses this to formally identify $\mathbb {C}$ formally as $\mathbb {R} ^{2}$ with the appropriate complex multiplication and then set $\mathrm {i} :=(0,1)^{\mathrm {T} }$ . In doing so, it is simultaneously defined:

The rotation of the complex plane at the origin by the positive angle $+{\tfrac {\pi }{2}}$ transforms the positive real into the positive imaginary unit $+{\mathrm {i}}$ .
If the positive-real semi-axis goes to the right in the complex plane, then you put the positive-imaginary semi-axis upwards. This is in accordance with the mathematical-positive sense of rotation.

The body extension $\mathbb {C} :\mathbb {R}$ is of degree $[\mathbb {C} :\mathbb {R} ]=2$ ; more precisely, $\mathbb {C}$ is isomorphic to the factor ring $\R[X]/(X^2+1)$ , where the minimal polynomial of $\mathrm {i}$ over $\mathbb {R}$ . Furthermore, $\mathbb {C}$ already forms the algebraic closure of $\mathbb {R}$ .
As $\mathbb {R}$ vector space, $\mathbb {C}$ the basis $\{1, \mathrm{i}\}$ . Besides, $\mathbb {C}$ as any body is also a vector space over itself, i.e. a one-dimensional $\mathbb {C}$ -vector space with base $\{1\}$ .
$\mathrm {i}$ and $-\mathrm{i}$ are exactly the solutions of the quadraticequation . In this sense, $\mathrm {i}$ (but also $\mathrm {-i}$ ) can be understood as "root of ".
$\mathbb {C}$ in contrast to $\mathbb {R}$ not an ordered body, i.e., there is no linear order relation on $\mathbb {C}$ . Therefore, one cannot meaningfully (in terms of addition and multiplication in $\mathbb {C}$ ) which of the two is the larger or the smaller number.

Amount and metric

Amount

The magnitude |z| of a complex number is the length of its vector in the Gaussian number plane and can be expressed, for example, by

$|z| = \sqrt{a^2 + b^2}$

from its real part $\operatorname{Re}{(z)}=a$ and imaginary part $\operatorname{Im}{(z)}=b$ . As a length, the magnitude is real and non-negative.

Examples:

$|4+3\mathrm {i} |={\sqrt {4^{2}+3^{2}}}={\sqrt {16+9}}={\sqrt {25}}=5$

$|239+\mathrm i| = \sqrt{239^2+1^2} = \sqrt{57121+1} = \sqrt{57122} = 169\cdot\sqrt{2}$

Metrics

The metric induced by the distance function $d_{\mathbb {C} }(z_{1},z_{2}):=|z_{1}-z_{2}|$ induced metric provides the complex vector space $\mathbb {C}$ with its standard topology. It coincides with the product topology of $\R \times \R$ as does the constraint $d_{\R}$ from $d_{\mathbb {C} }$ on $\mathbb {R}$ the standard metric on $\mathbb {R}$ .

Both spaces $\mathbb {C}$ like $\mathbb {R}$ are complete under these metrics. On both spaces, the topological notion of continuity can be extended to analytic notions such as differentiation and integration.

Complex number plane

While the set $\mathbb {R}$ of the real numbers can be illustrated by points on a number line, the set $\mathbb {C}$ of the complex numbers as points in a plane (complex plane, Gaussian number plane). This corresponds to the "double nature" of $\mathbb {C}$ as a two-dimensional real vector space. The subset of real numbers forms the horizontal axis, the subset of purely imaginary numbers (i.e. with real part 0) forms the vertical axis. A complex number $z = a+b\,\mathrm{i}$ with $a,b \in \R$ then has the horizontal coordinate and the vertical coordinate , is thus (a,b) identified with the number pair

According to the definition, the addition of complex numbers corresponds to vector addition, whereby one identifies the points in the number plane with their location vectors. Multiplication is a rotational extension in the Gaussian plane, which will become clearer after the introduction of the polar form below.

Polarform

If instead of the Cartesian coordinates $a=\operatorname {Re} (z)$ and $b=\operatorname {Im} (z)$ polar coordinates r = |z| and φ $\varphi =\arg(z)$ with $\arg$ as the argument function, the complex number can $z=a+b\,\mathrm{i}$ also be represented in the following so-called polar form (also polar representation) based on the Eulerian relation

$z=r\cdot \mathrm {e} ^{\mathrm {i} \varphi }=r\cdot (\cos \varphi +\mathrm {i} \cdot \sin \varphi )$

which $b = r \cdot \sin \varphi$ results from $a = r \cdot \cos \varphi$ and The representation using the complex e-function $r\cdot \mathrm {e} ^{\mathrm {i} \varphi }$ is also called exponential representation (of the polar form), the representation by means of the expression $r \cdot (\cos \varphi + \mathrm{i} \cdot \sin \varphi)$ trigonometric representation (of the polar form). Due to the Eulerian relation, both representations are equivalent. Furthermore, there are for them, namely in practice, the shortened notations

$z = r \cdot\operatorname{cis}\,\varphi = r \cdot\operatorname{E}\,(\varphi) = r\,\angle\,\varphi\,,$

in which $\operatorname{cis}\, \varphi$ for the sum $\cos \varphi + \mathrm{i} \cdot \sin \varphi$ and the representation with the angle operator $\angle$ called the versor representation.

In the complex number plane, corresponds to the Euclidean vector length (i.e. the distance to the origin 0) and φ $\varphi$ angle of the number enclosed by the real axis. Usually, however, called here the absolute value of (or its modulus) (notation r = |z| ) and the angle φ $\varphi$ the argument (or phase) of (notation φ $\varphi = \operatorname{arg}(z)$ ).

Since φ $\varphi$ and φ $\varphi+2\pi$ can be assigned to the same number , the polar representation is initially ambiguous. Therefore one $\varphi$ usually restricts φ the interval , $(-\pi;\pi]$ i.e. $z\neq 0$ $-\pi < \varphi \leq \pi$ to subsequently speak of its principal value for z ≠ instead of the argument itself. The number z=0 however, could be assigned to any argument, and for the purpose of an unambiguous representation it can in this case actually be set to 0.

The argument of is also the imaginary part of the complex natural logarithm

$\ln z=\ln|z|+\mathrm i\cdot\arg (z).$

With the choice of a branch of the on the whole of $\mathbb {C}$ is defined, an argument function is also determined (and vice versa).

All values $\mathrm {e} ^{\mathrm {i} \varphi }$ form the unit circle of the complex numbers with the absolute value , these numbers are also called unimodular and form the circle group.

That the multiplication of complex numbers (other than zero) corresponds to rotational extensions can be expressed mathematically as follows: The multiplicative group $\mathbb {C} ^{\times }$ of the complex numbers without the zero can be conceived as the direct product of the group of rotations, the circular group, and the extensions by a non-zero factor, the multiplicative group $\R^+$ . The former group can be $\varphi$ parameterised by the argument φ latter just corresponds to the amounts.

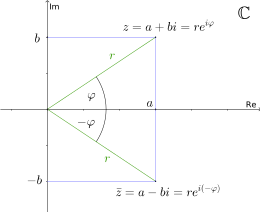
Complex conjugation

→ Main article: Conjugation (mathematics)

If one changes the sign of the imaginary part of a complex number $z = a+b\,\mathrm{i},$ one obtains the complex number conjugated to $\bar z=a-b\,\mathrm{i}$ (sometimes also written z^* ).

The conjugation $\mathbb {C} \to \mathbb {C} ,\,z\mapsto {\bar {z}}$ is an (involutory) body automorphism since it is compatible with addition and multiplication, i.e., for all $y,z\in \mathbb {C}$ holds

$\overline{y+z}=\bar y+\bar z,\quad \overline{y\cdot z}=\bar y\cdot \bar z.$

In the polar representation the conjugate complex number ${\bar {z}}$ with unchanged magnitude has just the negative angle of Thus, conjugation in the complex number plane can be interpreted as the reflection on the real axis. In particular, under conjugation, exactly the real numbers are mapped onto themselves.

The product of a complex number $z=a+b\,\mathrm{i}$ and its complex conjugate ${\bar {z}}$ is the square of its magnitude:

$z\cdot {\bar {z}}=(a+b\,\mathrm {i} )(a-b\,\mathrm {i} )=a^{2}+b^{2}=|z|^{2}$

The complex numbers thus form a trivial example of a C*-algebra.

The sum of a complex number $z=a+b\,\mathrm{i}$ and its complex conjugate ${\bar {z}}$ is 2 times its real part:

$z+{\bar {z}}=(a+b\,\mathrm {i} )+(a-b\,\mathrm {i} )=2a=2\,\operatorname {Re} {(z)}$

The difference between a complex number $z=a+b\,\mathrm{i}$ and its complex conjugate ${\bar {z}}$ is $\mathrm {2i}$ times its imaginary part:

$z-{\bar {z}}=(a+b\,\mathrm {i} )-(a-b\,\mathrm {i} )=2b\,\mathrm {i} =2\,\mathrm {i} \,\operatorname {Im} {(z)}$

Conversion formulae

From algebraic form to polar form

For $z=a+b\,\mathrm{i}$ in algebraic form is

$r = |z| = \sqrt{a^2 + b^2}=\sqrt{z \cdot \overline z}.$

For $z=0\quad (\Longleftrightarrow r=0)$ the argument φ is $\varphi$ arbitrary, but is often set to 0 or left undefined. For $z \neq 0$ the argument φ can be set in $\varphi$ the interval $(-\pi;\pi]$ with the aid of a trigonometric inverse function, for example with the aid of the arc cosine

$\varphi =\arg(z)={\Biggl \{}{\begin{matrix}\\\\\end{matrix}}{\Biggr .}$	$\arccos {\frac {a}{r}}$	for $b\geq 0$	${\Biggl .}{\begin{matrix}\\\\\end{matrix}}{\Biggr \}}\;=\operatorname {arctan2} (a,b)$
	$-\arccos {\frac {a}{r}}$	for

can be determined. Methods that use the arctangent are listed in the article Arc tangent and arc cotangent § Conversion of plane Cartesian coordinates into polar ones. This also includes the variant of the arctangent function often called arctan2, but also atan2, which is available in many programming languages and spreadsheets and which is passed both values and assigns the result to the appropriate quadrant depending on the sign of and

The calculation of the angle φ $\varphi$ in the interval $[0,2\pi)$ can in principle be done in such a way that the angle is first calculated as described above in the interval $(-\pi ,\pi ]$ calculated and then $2\pi$ increased by if it is negative:

$\varphi' = \arg(z) = \begin{cases} \varphi + 2\pi & \text{falls}\ \varphi < 0\\ \varphi & \text{sonst} \end{cases}$

(see polar coordinates).

From polar form to algebraic form

$a=\operatorname {Re} (z)=r\cdot \cos \varphi$

$b=\operatorname {Im} (z)=r\cdot \sin \varphi$

As above, the real part and the imaginary part of that complex number.

Arithmetic operations in the polar form

The following operands are to be linked together by arithmetic operations:

$z_{1}=r_{1}\cdot (\cos \varphi _{1}+\mathrm {i} \cdot \sin \varphi _{1})=r_{1}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{1}}$

$z_{2}=r_{2}\cdot (\cos \varphi _{2}+\mathrm {i} \cdot \sin \varphi _{2})=r_{2}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{2}}$

In multiplication, the amounts $r_{1}$ and are $r_{2}$ multiplied together and the corresponding phases φ $\varphi_1$ or φ $\varphi_2$ added. For division, the amount of the dividend is divided by the amount of the divisor and the phase of the divisor is subtracted from the phase of the dividend. There is also a somewhat more complicated formula for addition and subtraction:

Trigonometric form

${z_{1}\cdot z_{2}=r_{1}\cdot r_{2}\cdot \left[\cos(\varphi _{1}+\varphi _{2})+\mathrm {i} \cdot \sin(\varphi _{1}+\varphi _{2})\right]}$

${\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\cdot \left[\cos(\varphi _{1}-\varphi _{2})+\mathrm {i} \cdot \sin(\varphi _{1}-\varphi _{2})\right]$

$z_{1}\pm z_{2}=t\cdot (\cos \chi +\mathrm {i} \cdot \sin \chi )$

where $t:={\sqrt {r_{1}^{2}+r_{2}^{2}\pm 2r_{1}r_{2}\cos(\varphi _{1}-\varphi _{2})}},$
$\chi :=\operatorname {arctan2} \left(r_{1}\cos \varphi _{1}\pm r_{2}\cos \varphi _{2},r_{1}\sin \varphi _{1}\pm r_{2}\sin \varphi _{2}\right)$
and the arctan2 function.

Exponential form

$z_{1}\cdot z_{2}=r_{1}\cdot r_{2}\cdot \mathrm {e} ^{\mathrm {i} (\varphi _{1}+\varphi _{2})}$
${\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\cdot \mathrm {e} ^{\mathrm {i} (\varphi _{1}-\varphi _{2})}$
$z_{1}\pm z_{2}=t\cdot \mathrm {e} ^{\mathrm {i} \chi }$ with and χ $\chi$ as above.

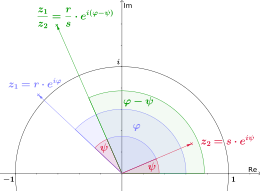
The division of two complex numbers corresponds to subtracting the angles and dividing the amounts.

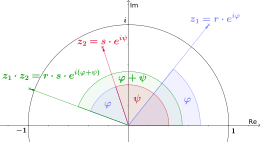
Multiplying two complex numbers is the same as adding the angles and multiplying the amounts.

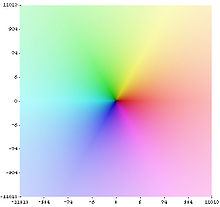
A complex number $z = a+b\,\mathrm{i}$ and the complex number conjugate to it $\bar z=a-b\,\mathrm{i}$

The colour representation of the complex number plane is often used to illustrate complex functions (here: the identity). The colour encodes the argument $\arg$ and the brightness indicates the amount $|\cdot |$

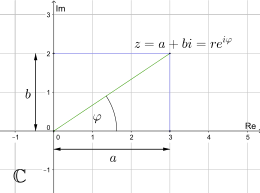
Gaussian plane with a complex number in Cartesian coordinates (a,b) and in polar coordinates (r,φ)

Arithmetic operations 3rd level

Third-level arithmetic operations include exponentiation, root extraction (root extraction) and logarithmisation.

Powers

Natural exponents

For natural numbers the th power is calculated in the polar form $z=r\mathrm {e} ^{\mathrm {i} \varphi }$ to

$z^{n}=r^{n}\cdot \mathrm {e} ^{\mathrm {i} n\varphi }=r^{n}\cdot (\cos n\varphi +\mathrm {i} \cdot \sin n\varphi )$

(see de Moivre's theorem) or for the algebraic form $z=a+b\,\mathrm {i}$ by means of the binomial theorem to

$z^{n}=\sum _{k=0, \atop k{\text{ gerade}}}^{n}{\binom {n}{k}}(-1)^{\frac {k}{2}}a^{n-k}b^{k}+\mathrm {i} \sum _{k=1, \atop k{\text{ ungerade}}}^{n}{\binom {n}{k}}(-1)^{\frac {k-1}{2}}a^{n-k}b^{k}.$

Any complex exponents

The general definition of a power with complex base $z\neq 0$ and complex exponent ω $\omega$ is as follows

$z^{\omega }:=\mathrm {e} ^{\omega \cdot \ln z},$

where $\ln(z)$ stands for the principal value of the complex logarithm (see below), thus the formula also yields a principal value. In the case ω $\omega \in \mathbb{Z}$ , however, all results in question agree with this main value and the function becomes unique.

Roots

→ Main article: Roots from complex numbers

Logarithms

The complex natural logarithm (unlike the real one on $\mathbb {R} ^{+}$ ) is not unique. A complex number is called the logarithm of the complex number if

$\mathrm {e} ^{w}=z.$

With also any number $w+2\pi \mathrm {i} k$ with any $k\in \mathbb {Z}$ a logarithm of . One therefore works with principal values, i.e. with values of a certain strip of the complex plane.

The principal value of the natural logarithm of the complex number

$z=r\mathrm {e} ^{\mathrm {i} \varphi }\in \mathbb {C} ^{\times }$

$\ln z=\ln r+\mathrm {i} \varphi$

with r>0 - π Put another way: The principal value of the natural logarithm of the complex number $z\in \mathbb {C} ^{\times }$ is

$\ln z=\ln |z|+\mathrm {i} \,\arg(z),$

where is $\arg(z)$ the principal value of the argument of

Obviously, the logarithm laws apply to the principal value of the natural logarithm only modulo $2\pi \mathrm {i} \mathbb {Z}$ .

The finite subgroups

All elements of a finite subgroup of the multiplicative unit group $\mathbb {C} ^{\times }=\mathbb {C} \setminus \{0\}$ are unit roots. Among all orders of group elements there is a maximum, say $n\in \mathbb {N}$ . Since $\mathbb {C}$ is commutative, an element with this maximum order then also generates the group, so that the group is cyclic and consists exactly of the elements

$\exp \left({2\pi \mathrm {i} k \over n}\right),\quad k=0,1,\dotsc ,n-1$

consists. All elements lie on the unit circle.

The union of all finite subgroups is a group isomorphic to the torsion group $\Q/\Z$ is isomorphic. It lies close in its completion, the already mentioned circle group, which can also be conceived as a 1-sphere and is isomorphic to $\mathbb{R} /\mathbb{Z }$ is isomorphic.

Pragmatic calculation rules

The easiest way to do the calculations is as follows:

Addition and subtraction of complex numbers are performed (in the algebraic form) component-wise.
The multiplication of complex numbers can be carried out advantageously in algebraic form or in exponential form (multiplication of the amounts and addition of the arguments (angles)), depending on the specification.
When dividing complex numbers, in exponential form their amounts are divided and their arguments (angles) subtracted, or in algebraic form the quotient is expanded with the conjugate denominator.
When exponentiating a complex number with a real exponent, its magnitude is exponentiated and its argument (angle) is multiplied by the exponent; using the algebraic form (with Newton's binomial theorem) is more cumbersome in most cases (especially for higher powers).
When a complex number with a real exponent is squared (root extraction), its absolute value is squared and its argument (angle) is divided by the exponent. This produces the first solution. An th root gives solutions distributed at an angle of $2\pi/n$ around the origin of the Gaussian plane. See square root (mathematics). A square root can also be calculated quite easily in Cartesian form.
When multiplying in algebraic form, one of the four multiplications can be saved by the following procedure. However, three additional additions or subtractions are necessary and the calculation is more difficult to parallelise.

$p_{1}=(a-b)(c+d)$

$p_{2}=bc$

$p_{3}=ad$

$\operatorname {Re} (z_{1}z_{2})=p_{1}+p_{2}-p_{3}$

$\operatorname {Im} (z_{1}z_{2})=p_{2}+p_{3}$

Construction of the complex numbers

In this section it is proved that indeed a body $\mathbb {C}$ of the complex numbers exists which satisfies the properties required in the above definition. Different constructions are possible, but they lead to the same body except for isomorphism.

Pairs of real numbers

The construction initially makes no reference to the imaginary unit $\mathrm {i}$ : In the 2-dimensional real vector space $\mathbb {R} ^{2}$ of ordered real number pairs z=(a,b) , besides the addition

$(a,b)+(c,d):=(a+c,b+d)$

(which is the ordinary vector addition) a multiplication by

$(a,b)\cdot (c,d):=(a\cdot c-b\cdot d,a\cdot d+b\cdot c)$

defined.

After this determination one writes $\mathbb {C} =\mathbb {R} ^{2}$ , and $(\mathbb {C} ,+,\cdot )$ becomes a body, the body of complex numbers. The imaginary unit is then $\mathrm {i} :=(0,1)$ defined by

Since $\{(1,0),(0,1)\}=\{1,\mathrm {i} \}$ a base of $\mathbb {R} ^{2}$ , thus be expressed as the linear combination

$z=1\cdot (a,0)+\mathrm {i} \cdot (b,0)=a+\mathrm {i} b$

represent.

First properties

The mapping $\mathbb {R} \to \mathbb {C} ,\,a\mapsto (a,0)$ is a body embedding of $\mathbb {R}$ in $\mathbb {C}$ due to which we identify the real number with the complex number

Regarding the addition is:

the number the neutral element (the zero element) in $\mathbb {C}$ and
the number the inverse element in $\mathbb {C}$ .

Regarding multiplication is:

the number the neutral element (the one-element) of $\mathbb {C}$ and
the inverse (reciprocal) of $z=(a,b)\neq (0,0)$ is $z^{-1} = \left(\frac{a}{a^2+b^2},\,\frac{-b}{a^2+b^2}\right)$ .

Reference to the representation in the form a + bi

By $\mathrm i:=(0,1)$ the imaginary unit is determined; for this $\mathrm {i} ^{2}=(0,1)^{2}=(-1,0)$ , which after the above embedding is equal to $-1\in \mathbb{R}$ corresponds.

Every complex number $z=(a,b)\in \mathbb {C}$ has the unique representation of the form

$z = (a,b) = (a,0)+(0,b)=a\cdot(1,0)+b\cdot(0,1) = a + b\,\mathrm{i}$

with $a,b\in\R$ ; this is the usual notation for the complex numbers.

Polynomials: Adjunction

Another construction of the complex numbers is the factor ring

$\R[X]/(X^2+1)$

of the polynomial ring in an indeterminate over the real numbers. The number $\mathrm {i}$ corresponds to the image of the indeterminate the real numbers are identified with the constant polynomials.

This principle of construction is also applicable in other contexts, one speaks of adjunction.

Matrices

The set of $2\times 2$ matrices of the form

$Z = \begin{pmatrix}a&-b\\b&a\end{pmatrix} = a \begin{pmatrix}1&0\\0&1\end{pmatrix} + b \begin{pmatrix}0&-1\\1&0\end{pmatrix} = a \cdot E + b \cdot I$ R $a,b\in\R$

also forms a model of the complex numbers. Here the real unit or the imaginary unit are represented $\mathrm {i}$ by the unit matrix or the matrix Therefore:

$\operatorname {Re}(Z)=a$

$\operatorname {Im}(Z)=b$

I^2 = -E

$\operatorname{abs}(Z) = \sqrt{a^2 + b^2} = \sqrt{\det Z}$

This set is a subspace of the vector space of real $2\times 2$ matrices.

Real numbers correspond to diagonal matrices $\begin{pmatrix}a&0\\0&a\end{pmatrix}.$

The linear mappings belonging to the matrices, unless and are both zero, are rotational extensions in the space $\mathbb {R} ^{2}$ . These are exactly the same rotational extensions as in the interpretation of multiplication by a complex number $a+b\mathrm i$ in the Gaussian number plane.

History

The term "complex numbers" was introduced by Carl Friedrich Gauss (Theoria residuorum biquadraticorum, 1831), the origin of the theory of complex numbers goes back to the Italian mathematicians Gerolamo Cardano (Ars magna, Nuremberg 1545) and Rafael Bombelli (L'Algebra, Bologna 1572; probably written between 1557 and 1560).

The impossibility of a naïve square of the kind $x^{2}=-1\Rightarrow x=\pm {\sqrt {-1}}$ noticed and emphasised very early in the treatment of quadratic equations, e.g. already in the algebra of Muhammed ibn Mûsâ Alchwârizmî written around 820 AD. But mathematical research did not stop at the obvious and incontestable conclusion that this type of equation could not be solved.

In a certain sense, the Italian Gerolamo Cardano (1501-1576) had already gone beyond this in his book Artis magnae sive de regulis algebraicis liber unus, published in 1545. There he deals with the task of finding two numbers whose product is 40 and whose sum is 10. He emphasises that the equation to be used for this is

x(10-x)=40

x^2-10x+40=0

has no solution, but adds some remarks by inserting in the solution

$x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {{\frac {p^{2}}{4}}-q}}$

of the general normalised quadratic equation

$x^{2}+px+q=0$

for and the values -10 and 40 respectively. So if it were possible to give the resulting expression

${\sqrt {25-40}}={\sqrt {-15}}$

in such a way that one would be allowed to calculate with this sign according to the same rules as with a real number, the expressions

$5 + \sqrt{-15}$

$5 - \sqrt{-15}$

indeed ever be a solution.

For the square root of negative numbers and more generally for all $\beta$ numbers composed of any real number α $\alpha$ and a positive real number β

$\alpha + \sqrt{-\beta}$ or α $\alpha - \sqrt{-\beta}$

Since the middle of the 17th century, the term imaginary number has become common, which originally came from René Descartes, who used it in his La Géométrie (1637) to express the difficulty of understanding complex numbers as non-real solutions of algebraic equations. John Wallis made the first advances in the 17th century with regard to a geometric interpretation of complex numbers. In 1702, Gottfried Wilhelm Leibniz called them a fine and wonderful refuge of the human mind, almost a hybrid between being and non-being. The introduction of the imaginary unit $\mathrm {i}$ as a new number is attributed to Leonhard Euler. He achieved valuable new insights by calculating with imaginary numbers, for example, he published Euler's formula in 1748 in his Introduction to Analysis and published explicitly for the first time the formula of Abraham de Moivre (at the end of the 17th century, he in turn had it from Isaac Newton), but even Euler still had great difficulties in understanding and classifying complex numbers, although he routinely calculated with them.

The geometric interpretation was first discovered by the Danish surveyor Caspar Wessel (published in 1799 in the Treatises of the Royal Danish Academy of Sciences, but not known to wider circles until about a hundred years later), by Jean-Robert Argand (in an obscure private print in 1806, but which came to Legendre's attention and became known to wider circles in 1813) and Gauss (unpublished). Gauss explicitly mentions the representation in a letter to Friedrich Bessel of 18 December 1811. After Argand, the geometric representation in the number plane is sometimes also called an Argand diagram.

Augustin-Louis Cauchy is considered the founder of complex analysis in a paper on integration in the complex submitted to the French Academy in 1814, but not published until 1825. In 1821, in his textbook Cours d'analyse, he defined a function of a complex variable in the complex number plane and proved many fundamental theorems of function theory.

Based on philosophical ideas of Immanuel Kant, William Rowan Hamilton found a logically sound justification of the complex numbers as an ordered pair of real numbers in 1833. He interpreted the complex number $a+b\cdot\mathrm i$ as a pair of numbers (a,b) and defined addition and multiplication by:

${\begin{aligned}(a_{1},b_{1})+(a_{2},b_{2})&=(a_{1}+a_{2},b_{1}+b_{2})\\(a_{1},b_{1})(a_{2},b_{2})&=(a_{1}a_{2}-b_{1}b_{2},a_{1}b_{2}+a_{2}b_{1})\end{aligned}}$

Today, these things do not cause any conceptual or actual difficulties. Due to the simplicity of the definition, the already explained meaning and applications in many scientific fields, the complex numbers are in no way inferior to the real numbers. The term "imaginary" numbers, in the sense of imaginary or unreal numbers, has thus developed over the centuries into a wry but retained designation.

Questions and Answers

Q: What is a complex number?

A: A complex number is a number made up of two parts, the first part being a real number and the second part being an imaginary number.

Q: What is the most important imaginary number?

A: The most important imaginary number is called i, which is defined as a number that will be -1 when squared.

Q: How are arithmetic functions used with complex numbers?

A: Arithmetic functions such as addition, subtraction, multiplication, and division can be used with complex numbers. They also follow commutative, associative and distributive properties just like real numbers.

Q: What symbol represents the set of complex numbers?

A: The set of complex numbers is often represented using the symbol C.

Q: Why were complex numbers discovered?

A: Complex numbers were discovered while attempting to solve special equations that have exponents in them because they posed real problems for mathematicians.

Q: Who introduced writing i for this type of number?

A: It was probably Leonhard Euler who introduced writing i for this type of number.

Q: How can a complex number be written as an ordered pair?

A: A complex number can be written as an ordered pair (a, b), where both a and b are real numbers.