Communes of the Haute-Corse department

The department of Haute-Corse is located in the region of Corsica in France. It is divided into three arrondissements with 236 communes (as of 1 January 2017).

See also: List of cantons in the department of Haute-Corse

Communes by department in France

Location of the department of Haute-Corse

[
{{7053}}]

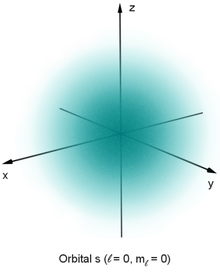
In the quantum mechanical models of atoms, an atomic orbital is the spatial wave function of a single electron in a quantum mechanical state, usually in a steady state. Its formula symbol is usually φ $\varphi$ (small phi) or ψ $\psi$ (small psi). The absolute square $|\psi ({\vec {r}})|^{2}$ describes as a density function the spatial distribution of the probability of the electron being ${\vec {r}}=(x,y,z)$ found at the location (Bornian probability interpretation of quantum mechanics). Together with the indication whether the spin is aligned parallel or antiparallel to a fixed axis or to the orbital angular momentum of the electron, an orbital completely describes the electron state.

In the older atomic models according to Niels Bohr (Bohr atomic model, 1913) and Arnold Sommerfeld (Bohr-Sommerfeld atomic model, 1916), an orbital describes an exact electron path selected by the quantisation rules. This idea was abandoned in quantum mechanics in favour of a diffuse distribution of the electron's residence probability. The quantum mechanical atomic orbital extends for bound electrons from the atomic nucleus in the centre outwards to infinity, where the residence probability asymptotically approaches zero. The most probable distance from the atomic nucleus for the innermost orbital is equal to the radius of the 1st Bohr circular orbit.

An orbital is usually represented by the surface of the smallest possible volume in whose interior the electron is located with a high (e.g. 90%) probability (see figure). One thus obtains bodies that correspond approximately to the size and shape of the atoms as they are noticeable in chemical molecules, condensed matter and the kinetic theory of gases.

The most common atomic orbitals are those that arise for the single electron of the hydrogen atom as solutions of the Schrödinger equation of the hydrogen problem and were first published in 1926. They have different forms $\psi _{nlm_{l}}({\vec {r}})$ denoted by ψ , where the lower index consists of the principal quantum number the orbital angular momentum quantum number and the magnetic quantum number $m_{l}$

In the orbital model for atoms with several electrons, it is assumed that the electrons distribute themselves among the orbitals taking into account the Pauli principle. Such a state is called the electron configuration and is often a useful approximation for the structure of the atomic shell, although this is further complicated by additional electron correlations.

To describe electrons in molecules, molecular orbitals are formed as linear combinations of atomic orbitals. Electrons in solids are described by orbitals that have the form of Bloch wave functions.

This article only deals with bound electrons in atoms. A simplification of the orbital model is the shell model.

Representation

Since the complete graphical representation of a wave function $\Psi \colon \mathbb {R} ^{3}\to \mathbb {R}$ required four dimensions (or five dimensions if $\Psi \colon \mathbb {R} ^{3}\to \mathbb {C}$ ), a complete representation in three dimensions is not directly possible (but, for example, with the aid of colour coding as in the table below). As is known from the hydrogen atom, the eigenfunctions $\Psi ({\vec {r}})$ of the stationary Schrödinger equation have $H\Psi ({\vec {r}})=E\Psi ({\vec {r}})$ a radial component R(r) and an angular component $Y_{l}^{m}(\theta ,\phi )$ :

$\Psi ({\vec {r}})=R(r)Y_{l}^{m}(\theta ,\phi )$

These proportions can be drawn separately. However, images of orbitals often show a representation of the probability density $|\Psi ({\vec {r}})|^{2}$ (and thus indirectly of the orbitals $\Psi ({\vec {r}})$ ). In a particularly obvious way, the probability density could be visualised as a cloud of points: If the probability density is large, many points are drawn; if the probability density is small, few points are drawn. However, since the probability density is not equal to zero at almost all points (except for the nodal points of the wave function) in space, an orbital cannot be completely represented in this way - since one would have to continue drawing points to infinity. Instead, one proceeds to draw isosurfaces of equal probability density, which are implicitly represented by

${\text{const}}=|\Psi ({\vec {r}})|^{2}=|R(r)|^{2}|Y_{l}^{m}(\theta ,\phi )|^{2}$

are defined. By sampling different angles θ $\theta ,\phi$ one learns something about the shape of the isosurface and thus something about the "shape of the orbital". The shape of the orbital is $Y_{l}^{m}(\theta ,\phi )$ given by a spherical surface function Often the constant is chosen so that the probability of finding the electron in the space enclosed by the isosurface is 90 %.

Not infrequently, when representing an isosurface of $|\Psi ({\vec {r}})|^{2}$ the surface is $\Psi ({\vec {r}})$ coloured according to the argument of as in the image of the p-orbital).

A simple way of schematically representing the occupation of atomic orbitals is the Pauling notation.

Representation of the probability density of the 1s orbital with the aid of a (very fine) point cloud

Quantum theory

→ Main article: Hydrogen problem

From the non-relativistic quantum theory, the orbitals result as follows: The interaction between electron and atomic nucleus is described by the Coulomb potential, the atomic nucleus is assumed to be fixed. The Hamilton operator for the one-electron system is

${\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+V(r)$

With the potential

$V(r)={\frac {Ze}{r}}$ .

Since the Hamiltonian operator commutes with the angular momentum operator, ${\hat {H}},$ ${\hat {l}}^{2}$ and ${\hat {l}}_{z}$ form a complete system of commuting observables. Thus, for these three operators there are common eigenstates $n,l,m_{l}$ determined by the three associated quantum numbers

The Schrödinger equation

${\hat {H}}\cdot \psi _{n,l,m_{l}}(r,\vartheta ,\phi )=E_{n,l,m_{l}}\cdot \psi _{n,l,m_{l}}(r,\vartheta ,\phi )$

can be decomposed into a radius-dependent and an angle-dependent part. The eigenfunctions ψ $\psi _{n,l,m_{l}}$ are the product of a spherical surface function $Y_{lm_{l}}(\vartheta ,\varphi )$ (eigenfunction of the angular momentum operator) and a radial function $\Phi _{nl}(r)\colon$

$\psi _{n,l,m_{l}}(r,\vartheta ,\phi )=Y_{lm_{l}}(\vartheta ,\varphi )\cdot \Phi _{nl}(r)$

These are shown normalised up to $n{\mathord {=}}3$ following table. Here $a_{0}$ denotes the Bohr radius and the nuclear charge number.

The orbitals shown in the following table are all aligned about the z-axis because they are eigenfunctions of the ${\hat {l}}_{z}$ operator. For alignment of an orbital with given orbital angular momentum in any other direction one has to $m_{l}$ form linear combinations of the wave functions to the different The graphical representation shows a volume on whose surface the residence probability density $|\psi ({\vec {r}})|^{2}$ is constant. The colours encode the complex phase of the wave function.

Complex wave functions in hydrogen-like atoms
Orbital	Wave function of the orbital				Shape of the orbital ψ $\psi ({\vec {r}})$ (not to scale)
			$m_{l}$	$\psi _{n,l,m_{l}}(r,\theta ,\phi )$
1s	1	0	00	${\frac {1}{\sqrt {\pi }}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}e^{-\textstyle {\frac {Zr}{a_{0}}}}$
2s	2	0	00	${\frac {1}{4{\sqrt {2\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}\left(2-{\frac {Zr}{a_{0}}}\right)e^{-\textstyle {\frac {Zr}{2a_{0}}}}$
2p0	2	1	00	${\frac {1}{4{\sqrt {2\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Zr}{a_{0}}}e^{-\textstyle {\frac {Zr}{2a_{0}}}}\cos \theta$
2p-1/+1	2	1	±1	${\frac {1}{8{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Zr}{a_{0}}}e^{-\textstyle {\frac {Zr}{2a_{0}}}}\sin \theta e^{\pm i\phi }$
3s	3	0	00	${\frac {1}{81{\sqrt {3\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}\left(27-18{\frac {Zr}{a_{0}}}+2{\frac {Z^{2}r^{2}}{a_{0}^{2}}}\right)e^{-\textstyle {\frac {Zr}{3a_{0}}}}$
3p0	3	1	00	${\frac {\sqrt {2}}{81{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}\left(6-{\frac {Zr}{a_{0}}}\right){\frac {Zr}{a_{0}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}\cos \theta$
3p-1/+1	3	1	±1	${\frac {1}{81{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}\left(6-{\frac {Zr}{a_{0}}}\right){\frac {Zr}{a_{0}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}\sin \theta e^{\pm i\phi }$
3d0	3	2	00	${\frac {1}{81{\sqrt {6\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Z^{2}r^{2}}{a_{0}^{2}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}(3\cos ^{2}\theta -1)$
3d-1/+1	3	2	±1	${\frac {1}{81{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Z^{2}r^{2}}{a_{0}^{2}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}\sin \theta \cos \theta e^{\pm i\phi }$
3d-2/+2	3	2	±2	${\frac {1}{162{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Z^{2}r^{2}}{a_{0}^{2}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}\sin ^{2}\theta e^{\pm 2i\phi }$

Natural orbital

A natural orbital is an orbital that does not result as an eigenfunction of a Hamiltonian operator, but as an eigenfunction of a single-electron density operator. This is obtained from a given many-particle state, which can also contain electron correlations, for example, and thus goes beyond the scope of a single-particle model. The electron configuration formed with the natural orbitals gives the best approximation to the initially given many-particle state that is possible with a single-particle model.

Time dependence

If orbitals are defined as eigenfunctions of an operator corresponding to an energy, then these orbitals are stationary within the framework of the chosen model. Examples of this are the Hartree-Fock orbitals as eigenfunctions of the Fock operator ${\hat {F}}$ and the Kohn-Sham orbitals, which are eigenfunctions of the Kohn-Sham Hamilton operator. In contrast, the so-called natural orbitals, as eigenfunctions of the reduced one-electron density operator, are non-stationary.

Hybridisation

Some symmetries of chemical bonds seem to contradict the characteristic shapes of the orbitals. These bonds can be understood by the formation of hybrid orbitals, which can form in the presence of electrons with different orbital angular momentum if they are energetically nearly equivalent (see above).

Multi-electron wave functions

The interpretation of orbitals as wave functions of one electron each is only possible unambiguously for single-electron systems. A wave function for N electrons can then be constructed by inserting N orbitals into a Slater determinant. This guarantees the antisymmetry of the entire wave function necessary for fermions, but cannot represent electron correlations beyond this. In order to also take the electron-electron interaction into account approximately, the orbitals can be determined by Hartree-Fock, Kohn-Sham calculations (see: Density Functional Theory in Quantum Physics) or MCSCF calculations (MCSCF: Multiconfiguration Self Consistent Field). However, it always remains valid that differently chosen orbitals, if they are linearly independent linear combinations of the original ones, mathematically result in the same Slater determinant, so that one cannot unambiguously infer from a given multi-particle wave function which are the individual occupied orbitals.

Representation of different orbitals of the first and second electron shell.
Top row: Representation of probability densities $|\Psi ({\vec {r}})|^{2}$ the orbitals as point clouds.
Bottom row: Representation of isosurfaces of $|\Psi ({\vec {r}})|^{2}$ . The isosurface is chosen in each case so that the electron has a 90 % probability of being within the volume enclosed by the isosurface.

Questions and Answers

Q: How many communes are there in the Haute-Corse department of France?

A: There are 236 communes in the Haute-Corse department of France.

Q: What are communes?

A: Communes in France are the smallest administrative division of the country.

Q: What is the Haute-Corse department?

A: The Haute-Corse department is a department in the northern part of the island of Corsica in France.

Q: What is the purpose of intercommunalities?

A: Intercommunalities in France are created to allow for cooperation between neighboring communes on issues of common interest.

Q: How many intercommunalities are there in Haute-Corse department?

A: The text does not specify the number of intercommunalities in the Haute-Corse department.

Q: What is the significance of the year 2018 mentioned in the text?

A: The year 2018 is mentioned as the latest year for which information about the intercommunalities is available.

Q: Can communes cooperate with each other outside of intercommunalities?

A: Yes, communes can cooperate with each other outside of intercommunalities as well.