Chi-squared distribution

The chi-square distribution or χ $\chi ^{2}$ distribution (older name: Helmert-Pearson distribution, after Friedrich Robert Helmert and Karl Pearson) is a continuous probability distribution over the set of non-negative real numbers. Usually, "chi-squared distribution" means the central chi-squared distribution. The chi-squared distribution has a single parameter, namely the number of degrees of freedom .

It is one of the distributions that ${\mathcal {N}}\left(\mu ,\sigma ^{2}\right)$ can be derived from the normal distribution Given random variables $Z_{i}$ that are independent and standard normally distributed, then the chi-squared distribution with degrees of freedom is defined as the distribution of the sum of squared random variables $Z_{1}^{2}+\dotsb +Z_{n}^{2}$ . Such sums of squared random variables occur in estimators such as sampling variance for estimating empirical variance. Thus, among other things, the chi-squared distribution allows a judgment to be made about the compatibility of a presumed functional relationship (dependence on time, temperature, pressure, etc.) with empirically determined measurement points. For example, can a straight line explain the data, or do we need a parabola or perhaps a logarithm? One chooses different models, and the one with the best goodness of fit, the smallest chi-square value, provides the best explanation of the data. Thus, by quantifying the random fluctuations, the chi-square distribution puts the choice of different explanatory models on a numerical basis. Moreover, once one has determined the empirical variance, it allows one to estimate the confidence interval that includes the (unknown) value of the variance of the population with some probability. These and other applications are described below and in the article Chi-Square Test.

The chi-squared distribution was introduced in 1876 by Friedrich Robert Helmert, the name comes from Karl Pearson (1900).

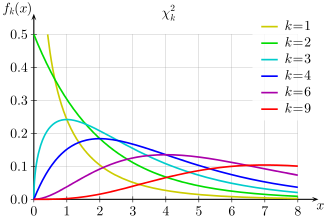
Densities of the chi-squared distribution with different number of degrees of freedom k

Definition

The square of a standard normally distributed random variable $Z\sim {\mathcal {N}}(0,1)$ follows a chi-squared distribution with one degree of freedom:

$Z^{2}\sim \chi ^{2}(1)$ .

Furthermore, if $X_{r_{1}},\dotsc ,X_{r_{n}}$ are jointly stochastically independent chi-squared distributed random variables, then their sum is chi-squared distributed with the sum of the respective degrees of freedom

$Y=X_{r_{1}}+\dotsb +X_{r_{n}}\sim \chi ^{2}(r_{1}+\dotsb +r_{n})$ .

Thus, the chi-squared distribution is reproducible. Let be $Z_{1},\dotsc ,Z_{n}$ stochastically independent and standard-normally distributed random variables, then their sum-of-squares that it is chi-squared distributed with the number of degrees of freedom :

$Q=Z_{1}^{2}+\dotsb +Z_{n}^{2}\;\sim \;\chi ^{2}(n)$ .

The character $\,\sim$ is a shorthand notation for "follows the distribution". For example, $Q\;\sim \;\chi ^{2}(n)$ ; also often written as $Q\;\sim \;\chi _{n}^{2}$ The random variable follows a chi-squared distribution with number of degrees of freedom . The sum of squared quantities cannot take negative values.

In contrast, for the simple sum $Z_{1}+\dotsb +Z_{n}\sim {\mathcal {N}}(0,n)$ with distribution symmetric about the zero point.

Density and distribution of multiple chi-square distributed random variables.

Density

The density $f_{n}$ of the χ $\chi_n^2$ distribution with degrees of freedom has the form:

$f_{n}(x)={\frac {1}{2^{\frac {n}{2}}\Gamma ({\tfrac {n}{2}})}}x^{{\frac {n}{2}}-1}\operatorname {exp} \left\{-{\frac {x}{2}}\right\}\quad ,x>0$

Here Γ $\Gamma (r)$ stands for the gamma function. The values of Γ $\Gamma ({\tfrac {n}{2}})$ can be calculated with

$\Gamma ({\tfrac {1}{2}})={\sqrt \pi }\;,\quad \Gamma (1)=1\;,$

$\Gamma (r+1)=r\cdot \Gamma (r)\quad {\text{mit}}\quad r\in \mathbb {R} ^{+}$ .

Calculate

Distribution function

The distribution function can be written using the regularized incomplete gamma function:

$F_{n}(x)=P({\tfrac n2},{\tfrac x2}).$

If is a natural number, then the distribution function can be represented (more or less) elementarily:

$P\left({\tfrac {n}{2}},{\tfrac {x}{2}}\right)=1-e^{-{\frac {x}{2}}}\sum \limits _{k=0}^{n/2-1}{\frac {1}{\Gamma (k+1)}}({\tfrac {x}{2}})^{k}\quad (n=2,4,\dotsc ),$

$P({\tfrac {n}{2}},{\tfrac {x}{2}})=\operatorname {Erf} \left({\sqrt {\tfrac {x}{2}}}\right)-e^{-{\frac {x}{2}}}\sum \limits _{k=0}^{\lfloor n/2\rfloor -1}{\frac {1}{\Gamma (k+{\tfrac {3}{2}})}}({\tfrac {x}{2}})^{k+{\tfrac {1}{2}}}\quad (n=1,3,\dotsc ),$

where $\operatorname {Erf}$ denotes the error function. The distribution function describes the probability that χ $\chi_n^2$ [0,x] lies in the interval

Properties

Expected value

The expected value of the chi-square distribution with degrees of freedom is equal to the number of degrees of freedom

$\operatorname {E}\left(\chi _{n}^{2}\right)=n$ .

Thus, assuming a standard normally distributed population, if the variance of the population is correctly estimated, the value χ $\chi _{n}^{2}/n$ should be close to 1.

Variance

The variance of the chi-square distribution with degrees of freedom is equal to 2 times the number of degrees of freedom

$\operatorname {Var}(\chi _{n}^{2})=2n$ .

Mode

The mode of the chi-squared distribution with degrees of freedom is n-2 for $n\ge 2$ .

Skew

The skewness γ $\gamma _{m}$ of the chi-squared distribution with degrees of freedom is

$\gamma _{m}(\chi _{n}^{2})={\frac {2{\sqrt {2}}}{\sqrt {n}}}$ .

The chi-square distribution has a positive skewness, i.e., it is left-skewed or right-skewed. The higher the number of degrees of freedom the less skewed the distribution is.

Kurtosis

The kurtosis (kurtosis) β $\beta _{2}$ of the chi-squared distribution with degrees of freedom is given by

$\beta _{2}=3+{\frac {12}{n}}$ .

The excess γ $\gamma_2$ over the normal distribution thus results in γ $\gamma _{2}={\tfrac {12}{n}}$ . Therefore, the higher the number of degrees of freedom , the lower the excess.

Moment generating function

The moment generating function for $X\sim \chi _{n}^{2}$ has the form

$M_X(t) = \frac{1}{(1-2 t)^{n/2}}$ .

Characteristic function

The characteristic function for $X\sim \chi _{n}^{2}$ from the moment generating function as:

$\varphi _{X}(s)={\frac {1}{(1-2is)^{{n/2}}}}$ .

Entropy

The entropy of the chi-squared distribution (expressed in nats) is

$H(X)=\ln \left(2\Gamma \left({\frac {n}{2}}\right)\right)+\left(1-{\frac {n}{2}}\right)\psi \left({\frac {n}{2}}\right)+{\frac {n}{2}},$

where ψ(p) denotes the digamma function.

Non-Central Chi-Square Distribution

If the normally distributed random variables are not $\mu _{i}(i=1,\ldots ,n)$ centered with respect to their expected value μ if not all μ $\mu _{i}=0$ ), the noncentral chi-squared distribution is obtained. It has as a second parameter besides the noncentrality parameter λ

Let $Z_{i}\sim {\mathcal {N}}(\mu _{i},1),\,i=1,2,\ldots ,n$ , then

$\sum _{{i=1}}^{n}{Z_{i}}^{2}\sim \chi ^{2}(n,\lambda )$ with λ $\lambda =\sum _{{i=1}}^{n}{\mu _{i}}^{2}$ .

In particular, it follows from $\,X\sim \chi ^{2}(n-1)$ and $Z\sim {\mathcal {N}}({\sqrt {\lambda }},1)$ that $\,X+Z^{2}\sim \chi ^{2}(n,\lambda )$ is

A second way to generate a non-central chi-squared distribution is as a mixture distribution of the central chi-squared distribution. Here is

$\chi ^{2}(n+2\,j)=\chi ^{2}(n,\lambda )$ ,

if is drawn $j\sim {\mathcal {P}}\left({\tfrac {\lambda }{2}}\right)$ from a Poisson distribution.

Density function

The density function of the non-central chi-squared distribution is

$f(x)={\frac {\operatorname {exp} \left\{-{\frac {1}{2}}(x+\lambda )\right\}}{2^{\frac {n}{2}}}}\,\sum _{j=0}^{\infty }{\frac {x^{{\frac {n}{2}}+j-1}\lambda ^{j}}{2^{2j}\,\Gamma \left({\frac {n}{2}}+j\right)\,j!}}$ for $x\geq 0$ , $\,f(x)=0$ for

The sum over j leads to a modified Bessel function of first genus $I_{q}(x)$ . This gives the density function the following form:

$f(x)={\frac {\operatorname {exp} \left\{-{\frac {1}{2}}(x+\lambda )\right\}x^{{\frac {1}{2}}(n-1)}{\sqrt {\lambda }}}{2(\lambda x)^{\frac {n}{4}}}}\,I_{{\frac {n}{2}}-1}\left({\sqrt {\lambda x}}\right)$ for $x\geq 0$ .

Expected value and variance of the noncentral chi-squared distribution $n+\lambda$ and $2n+4\lambda$ into the corresponding expressions of the central chi-squared distribution, as does the density itself when λ $\lambda \to 0$

Distribution function

The distribution function of the noncentral chi-squared distribution can be $Q_{M}(a,b)$ expressed using the Marcum function Q

$F(x)=1-Q_{{{\frac {n}{2}}}}\left({\sqrt {\lambda }},{\sqrt {x}}\right)$

Example

Take measurements of a quantity , which come from a normally distributed population. Let be ${\overline {x}}$ the empirical mean of the measured values and

$s^{2}={\frac {1}{n-1}}\sum _{{k=1}}^{n}(x_{k}-\overline {x})^{2}$

the corrected sample variance. Then, for example, the 95% confidence interval for the variance of the population σ $\sigma ^{2}$ specified:

${\tfrac {n-1}{\chi _{b}^{2}}}\,s^{2}\leq \sigma ^{2}\leq {\tfrac {n-1}{\chi _{a}^{2}}}\,s^{2},$

where χ $\chi _{b}^{2}$ by $F_{{n-1}}(\chi _{b}^{2})=0{,}975$ and χ $\chi _{a}^{2}$ by $F_{{n-1}}(\chi _{a}^{2})=0{,}025$ , and therefore also χ $\chi _{a}^{2}\leq n-1\leq \chi _{b}^{2}$ . The limits follow from the fact that ${\tfrac {(n-1)s^{2}}{\sigma ^{2}}}$ $\chi _{{n-1}}^{2}$ is distributed as χ

Derivation of the distribution of the sample variance

Let $x_{{1}},\dots ,x_{{n}}$ a sample of measurements, drawn from a normally distributed random variable with empirical mean ${\overline {x}}={\tfrac {1}{n}}\sum _{i=1}^{n}x_{i}$ and sample variance $s^{2}={\tfrac {1}{n-1}}\sum _{{i=1}}^{n}(x_{i}-\overline {x})^{2}$ as estimators for expected value μ $\mu$ and variance σ $\sigma ^{2}$ the population.

Then it can be shown, that ${\tfrac {(n-1)s^{2}}{\sigma ^{2}}}=\sum _{{i=1}}^{n}{\tfrac {(x_{i}-\overline {x})^{2}}{\sigma ^{2}}}$ is distributed as χ $\chi _{{n-1}}^{2}$ .

To do this, Helmert $(y_{j})$ transforms the into new variables $(x_{i})$ using an orthonormal linear combination. The transformation is:

$y_{{1}}={\tfrac {1}{{\sqrt {2}}}}x_{{1}}-{\tfrac {1}{{\sqrt {2}}}}x_{{2}}$

$y_{{2}}={\tfrac {1}{{\sqrt {6}}}}x_{{1}}+{\tfrac {1}{{\sqrt {6}}}}x_{{2}}-{\tfrac {2}{{\sqrt {6}}}}x_{{3}}$

$\vdots$

$y_{{n-1}}={\tfrac {1}{{\sqrt {n(n-1)}}}}x_{{1}}+{\tfrac {1}{{\sqrt {n(n-1)}}}}x_{{2}}+\dotsb +{\tfrac {1}{{\sqrt {n(n-1)}}}}x_{{n-1}}-{\tfrac {n-1}{{\sqrt {n(n-1)}}}}x_{{n}}$

$y_{n}={\tfrac {1}{\sqrt {n}}}x_{1}+{\tfrac {1}{\sqrt {n}}}x_{2}+\dotsb +{\tfrac {1}{\sqrt {n}}}x_{n-1}+{\tfrac {1}{\sqrt {n}}}x_{n}={\sqrt {n}}\,{\overline {x}}.$

The new independent variables $y_{i}$ are normally distributed like with equal variance σ $\sigma _{{y_{i}}}^{2}=\sigma _{{x_{i}}}^{2}=\sigma ^{2},(i=1,\dots ,n)$ , but with expected value ${\mathrm {E}}(y_{i})=0,(i=1,\dots ,n-1),$ both due to the convolution invariance of the normal distribution.

Moreover, for the coefficients $a_{{ij}}$ in $y_{{i}}=\sum _{{j=1}}^{n}a_{{ij}}x_{{j}}$ (if j>i+1 , $a_{{ij}}=0$ ) because of orthonormality $\sum _{{i=1}}^{n}a_{{ij}}a_{{ik}}=\delta _{{jk}}$ (Kronecker delta) and thus

$\sum _{{i=1}}^{n}y_{{i}}^{2}=\sum _{{i=1}}^{n}\sum _{{j=1}}^{n}a_{{ij}}x_{{j}}\sum _{{k=1}}^{n}a_{{ik}}x_{{k}}=\sum _{{j=1}}^{n}\sum _{{k=1}}^{n}\delta _{{jk}}x_{{j}}x_{{k}}=\sum _{{j=1}}^{n}x_{{j}}^{2}.$

Therefore, the sum of the squares of the deviations is now given by

$(n-1)s^{2}=\sum _{{i=1}}^{n}(x_{i}-\overline {x})^{2}=\sum _{{i=1}}^{n}x_{{i}}^{2}-n\overline {x}^{2}=\sum _{{i=1}}^{n}y_{{i}}^{2}-y_{{n}}^{2}=\sum _{{i=1}}^{{n-1}}y_{{i}}^{2}$

and finally after division by σ $\sigma ^{2}$

$(n-1){\frac {s^{2}}{\sigma ^{2}}}=\sum _{{i=1}}^{{n-1}}{\frac {y_{i}^{2}}{\sigma ^{2}}}.$

The expression on the left hand side is apparently distributed like a sum of squared standard normally distributed independent variables with n-1 summands, as required for χ $\chi _{{n-1}}^{2}$

Thus, the sum is chi-squared distributed with n-1 degrees of freedom $\sum _{{i=1}}^{n}\left({\tfrac {x_{i}-\overline {x}}{\sigma }}\right)^{2}\sim \chi _{{n-1}}^{2}$ , while by definition of the chi-squared sum $\sum _{{i=1}}^{n}\left({\tfrac {x_{i}-\mu }{\sigma }}\right)^{2}\sim \chi _{{n}}^{2}$ . One degree of freedom is "consumed" here, because due to the centroid property of the empirical mean $\sum \nolimits _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)=0$ the last variation is $\left(x_{n}-{\overline {x}}\right)$ already (n-1) determined by the first Consequently, only (n-1) variances vary freely and one therefore averages the empirical variance by (n-1) dividing by the number of degrees of freedom

Relationship to other distributions

Relationship to gamma distribution

The chi-squared distribution is a special case of the gamma distribution. If $X\sim \chi _{n}^{2}$ , then

$X\sim \gamma ({\tfrac {n}{2}},{\tfrac {1}{2}}).$

Relationship to normal distribution

Let $Z_{1},\dotsc ,Z_{n}$ be independent and standard normally distributed random variables, then their sum of squares that it is chi-squared distributed with the number of degrees of freedom :

$Q=Z_{1}^{2}+\dotsb +Z_{n}^{2}\;\sim \;\chi ^{2}(n)$ .

For $n\geq 30$ , is $Y={\sqrt {2X}}-{\sqrt {2n-1}}$ approximately standard normally distributed.

For the random variable X n {\displaystyle $X_{n}$ normally distributed, with expected value n {\displaystyle n} standard deviation 2 n {\displaystyle for a noncentral chi-squared distribution with expected value $n+\lambda$ and standard deviation ${\sqrt {2n+4\lambda }}$ .

Relationship to exponential distribution

A chi-squared distribution with 2 degrees of freedom is an exponential distribution $\operatorname {Exp}(\lambda )$ with parameter λ $\,\lambda =1/2$ .

Relationship to Erlang distribution

A chi-squared distribution with degrees of freedom is identical to an Erlang distribution $\operatorname {Erl}(\lambda ,n)$ with degrees of freedom and λ $\,\lambda =1/2$ .

Relationship to F-Distribution

Let χ $\chi ^{2}(r_{1})$ and χ be $\chi ^{2}(r_{2})$ independent chi-squared distributed random variables with $r_{1}$ and $r_{2}$ degrees of freedom, then the quotient is

$F={\frac {\chi ^{2}(r_{1})/r_{1}}{\chi ^{2}(r_{2})/r_{2}}}$

F-distributed with $r_{1}$ numerator degrees of freedom and $r_{2}$ denominator degrees of freedom.

Relationship to Poisson distribution

The distribution functions of the Poisson distribution and the chi-square distribution are related in the following way:

The probability of finding or more events in an interval within which one expects on average λ $\lambda$ events is like the probability that the value of χ $\chi_{2n}^2\leq 2\lambda$ Namely, it holds

$1 - Q(n, \lambda ) = P(n, \lambda )$ ,

with and as regularized gamma functions.

Relationship to continuous uniform distribution

For even one can n=2m form the χ $\chi_n^2$ -distribution as an -fold convolution using the uniformly continuous density U(0,1) :

$\chi _{n}^{2}=-2\ln {\left(\prod _{{i=1}}^{m}u_{i}\right)}=-2\sum _{{i=1}}^{m}\ln(u_{i})$ ,

where the $u_{i}$ are independent uniformly continuously distributed random variables.

For odd , however, the following applies

$\chi _{n}^{2}=\chi _{{n-1}}^{2}+\left[{\mathcal {N}}(0,1)\right]^{{2}}.$

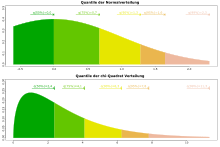
Quantiles of a normal distribution and a chi-square distribution

Derivation of the density function

The density of the random variable χ $\chi _{n}^{2}=X_{1}^{2}+\dotsb +X_{n}^{2}$ , with $X_{1},\dots ,X_{n}$ independent and standard normally distributed, is given by the joint density of the random variables $X_{1},\dots ,X_{n}$ . This joint density is the -fold product of the standard normal distribution density:

$f_{{X_{1},\dots ,X_{n}}}(x_{1},\dots ,x_{n})=\prod _{{i=1}}^{n}{\frac {e^{{-{\frac 12}x_{i}^{2}}}}{{\sqrt {2\pi }}}}=(2\pi )^{{-{\frac n2}}}e^{{-{\frac 12}(x_{1}^{2}+\dotsb +x_{n}^{2})}}.$

For the density we are looking for:

${\begin{aligned}f_{{\chi _{n}^{2}}}(z)&=\lim _{{h\to 0}}{\frac 1h}P(z<\chi _{n}^{2}\leq z+h)\\&=\lim _{{h\to 0}}{\frac 1h}\int \limits _{K}(2\pi )^{{-{\frac n2}}}e^{{-{\frac 12}(x_{1}^{2}+\dotsb +x_{n}^{2})}}\,dx_{1}\ldots dx_{n}\\&=(2\pi )^{{-{\tfrac n2}}}e^{{-{\frac z2}}}\lim _{{h\to 0}}{\frac 1h}\int \limits _{K}dx_{1}\ldots dx_{n}\\\end{aligned}}$

where $K=\{z\leq x_{1}^{2}+\dotsb +x_{n}^{2}\leq z+h\}.$

In the limit, the sum in the argument of the exponential function is equal to . It can be shown that the integrand can be drawn as $(2\pi )^{-{\tfrac {n}{2}}}e^{-{\frac {z}{2}}}$ before the integral and the limit.

The remaining integral

$\int \limits _{K}dx_{1}\ldots dx_{n}=V_{n}({\sqrt {z+h}})-V_{n}({\sqrt z})$

corresponds to the volume of the shell between the sphere with radius ${\sqrt {z+h}}$ and the sphere with radius ${\sqrt z}$ ,

where gives $V_{n}(R)={\frac {\pi ^{{{\frac n2}}}R^{n}}{\Gamma ({\frac n2}+1)}}$ the volume of the n-dimensional sphere with radius R.

It follows: $\lim _{h\to 0}{\frac {1}{h}}\int \limits _{K}dx_{1}\ldots dx_{n}={\frac {\mathrm {d} \,V_{n}({\sqrt {z}})}{\mathrm {d} \,z}}={\frac {\pi ^{\tfrac {n}{2}}z^{{\tfrac {n}{2}}-1}}{\Gamma ({\tfrac {n}{2}})}}$

and after substituting into the expression for the density we are looking for:

Quantile function

The quantile function x_p the chi-squared distribution is the solution of the equation $p=P({\tfrac n2},{\tfrac {x_{p}}2})$ and thus in principle can be calculated via the inverse function. Concretely applies here

$x_{p}=2P^{{-1}}\left({\tfrac n2},p\right),$

with $P^{{-1}}$ as inverse of the regularized incomplete gamma function. This value x_p is entered in the quantile table under the coordinates and

Quantile function for small sample size

For a few values (1, 2, 4) one can also specify the quantile function alternatively:

$n=1:x_{p}=2(\operatorname {Erf}^{{-1}}(p))^{2},$

$n=2:x_{p}=-2\,\ln(1-p),$

$n=4:x_{p}=-2\,(1+W_{{-1}}(-(1-p)/e)),$

where $\operatorname {Erf}$ denotes the error function, $W_{{-1}}(x)\,$ denotes the lower branch of the Lambertian W-function, and denotes the Euler number.

Approximation of the quantile function for fixed probabilities

For certain fixed probabilities the associated quantiles x_p obtained by the simple sample size function

$x_{p}\approx n+a{\sqrt {n+\operatorname {sgn}(a){\sqrt {n}}}}+b+c/n$

with parameters a,b,c from the table, where $\operatorname{sgn}(a)$ denotes the signum function, which simply represents the sign of its argument:

0,005	0,01	0,025	0,05	0,1	0,5	0,9	0,95	0,975	0,99	0,995
−3,643	−3,298	−2,787	−2,34	−1,83	0	1,82	2,34	2,78	3,29	3,63
1,8947	1,327	0,6	0,082	−0,348	−0,67	−0,58	−0,15	0,43	1,3	2
−2,14	−1,46	−0,69	−0,24	0	0,104	−0,34	−0,4	−0,4	−0,3	0

Comparison with a χ $\chi ^{2}$ table shows n>3 relative error below 0.4% for and n > 10 n>10 Since the χ $\chi ^{2}$ -distribution for large transitions to a normal distribution with standard deviation ${\sqrt {2n}}$ , the parameter from the table, which has been freely adjusted here, at the corresponding probability approximately the size of ${\sqrt {2}}$ times the quantile of the normal distribution ( ${\sqrt {2}}\,\operatorname {Erf}^{{-1}}(2p-1)$ ), where $\operatorname {Erf}^{{-1}}$ denotes the inverse of the error function.

The 95% confidence interval for the variance of the population from the Example section can be obtained, e.g. with the two functions x_p from the lines with $p=0{,}025\to \chi _{a}^{2}$ and $p=0{,}975\to \chi _{b}^{2}$ plotted in a simple way as a function of .

The median is located in the column of the table with $p=0{,}5$ .

Chi-squared distribution

Definition

Density

Distribution function

Properties

Expected value

Variance

Mode

Skew

Kurtosis

Moment generating function

Characteristic function

Entropy

Non-Central Chi-Square Distribution

Density function

Distribution function

Example

Derivation of the distribution of the sample variance

Relationship to other distributions

Relationship to gamma distribution

Relationship to normal distribution

Relationship to exponential distribution

Relationship to Erlang distribution

Relationship to F-Distribution

Relationship to Poisson distribution

Relationship to continuous uniform distribution

Derivation of the density function

Quantile function

Quantile function for small sample size

Approximation of the quantile function for fixed probabilities

Search by letter