Capacitance

This article deals with the physical quantity from electrostatics. For the capacity of a battery, see capacity (galvanic cell).

The electrical capacitance (formula symbol from Latin capacitas 'capacity'; adjective capacitive) is a physical quantity from the field of electrostatics, electronics and electrical engineering.

The electrical capacitance between two electrically conductive bodies insulated from each other is equal to the ratio of the amount of charge stored on these conductors ( one and on the other) and the electric voltage between them. :

$C = \frac Q U$

It is determined by the dielectric constant of the insulating medium and the geometry of the bodies, including the distance. Thus (if the capacitance is constant) and proportional relationship to each other.

In the case of accumulators and batteries, the term "capacity" is used for the maximum charge quantity which can be stored in them. It is given in ampere-hours (Ah). However, this capacity of the electrical charge has nothing to do with the electrical capacity (farad) or the power capacity (watt) shown here.

Capacitance of a capacitor

Capacitance has a technical application in the form of electrical capacitors, which are characterized by the specification of a certain capacitance. The term "capacitance" is also used colloquially as a synonym for the electrical component capacitor itself.

Capacitors represent a conductor arrangement with two electrodes for separate storage of electric charge and In physical terms, the electric flow stems $\Psi$ from the separated electric charges and transported to the electrodes by the external voltage source with voltage , thus:

$Q=C\cdot U$

results. Formally, this relationship takes place via Gauss' law. The electrical capacitance of a capacitor can then be expressed as the ratio of the quantity of charge to the applied voltage

$C = \frac{Q}{U}$ .

Here, usually a constant parameter that is obtained as follows.

A body to which a positive electric charge is given thereby has an electric field which opposes the movement of another positive electric charge towards the body. However, if there is now a body nearby that is negatively charged, the repulsive electric field of the positive body is weakened (the positive charge moving towards the body also feels the force of the attracting negative charge). Thus, less voltage is needed to move the additional positive charge onto the already positively charged body than without the second negatively charged body. So the first body has a higher capacity. Of course, the same is true for the second body. The attenuation of the electric field through one charged body to the other charged body is influenced by their geometry and the permittivity of the insulating medium between the two bodies.

In a simplified analogy, the capacity corresponds to the volume of a compressed air tank with constant temperature. The air pressure is analogous to the voltage and the amount of air is analogous to the amount of charge . Therefore, the amount of charge in the capacitor is proportional to the voltage.

This law also applies to the so-called pseudocapacitance, an electrochemical or faraday storage of electrical energy that is voltage-dependent within narrow limits and is associated with a redox reaction and charge exchange at the electrodes of supercapacitors, although unlike accumulators, no chemical change occurs at the electrodes.

Among others, the Physikalisch-Technische Bundesanstalt (PTB) deals with capacitance standards.

Unit

Electrical capacitance is measured in the derived SI unit farad. A farad (1 F) is the capacitance that stores an amount of charge equal to 1 coulomb (1 C = 1 As) when a voltage of 1 volt is applied:

$[C]=\frac{[Q]}{[U]} = \frac{1\,\mathrm{C}}{1\,\mathrm{V}} = \frac{1\,\mathrm{As}}{1\,\mathrm{V}} = 1\,\mathrm{F}$

A capacitor with a capacity of 1 farad charges to a voltage of 1 volt in 1 second at a constant charging current of 1 ampere. The SI unit Farad, named in honor of the English physicist and chemist Michael Faraday, has now become internationally accepted everywhere.

Obsolete unit

Until the middle of the 20th century, the capacitance of capacitors was often labeled with the unit of capacitance cm. This indication in centimeters is due to the fact that the capacitance is expressed in the length dimension in the Gaussian system of units, which is practically no longer used today. Thus, a metal sphere with a radius of 5 cm has a capacitance of 5 cm compared to a counter electrode located at infinity.

The adjacent figure shows a paper capacitor of the SATOR brand of the former Kremenezky, Mayer & Co company from 1950 with a capacitance of 5000 cm. This corresponds to the capacitance of a metal sphere of 5000 cm radius. Represented in today's SI system of units, this is approx. 5.6 nF.

A capacitance of 1 cm in the Gaussian system of units is equivalent to about 1.1 pF in the SI system of units, and the conversion factor is 4πε0. This conversion comes about because of the definition of the field constant in the Gaussian system of units:

$\varepsilon_0 := \frac {1} {4 \pi}$ in the Gaussian system of units (not in the International System of Units (SI)).

Paper capacitor with the capacity 5000 cm.

Capacitance of certain conductor arrangements

For the capacitance of a series of simple ladder arrangements, there are analytical solutions or convergent series expansions. The following table shows some examples:

Designation	Capacity	Schematic representation
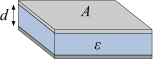
Plate capacitor	$C=\varepsilon \cdot {\frac {A}{d}}$
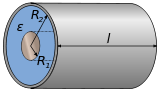
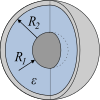
Coaxial cable or cylindrical capacitor	$C=2\pi \varepsilon \, \frac{l}{\ln\!\left(\frac{R_2}{R_1}\right)}$
Spherical capacitor	$C={\frac {4\pi \varepsilon }{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}}}$
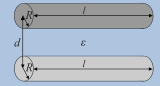
Sphere, counter electrode with $R_{2}$ towards infinity	$C = 4 \pi \varepsilon \cdot R_1$
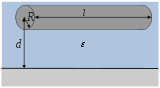
Parallel cylinder (Lecher line)	$C={\frac {\pi \varepsilon l}{\operatorname {arcosh}\left({\frac {d}{2R}}\right)}}$
A conductor in parallel over a flat surface.	$C = \frac{2\pi \varepsilon l}{\operatorname{arcosh}\left( \frac{d}{R}\right) }$	$d>R$
Two spheres with identicalradius	$C = 2\pi \varepsilon a\sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^2-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^2-1}\right) \right) }$ $=2\pi \varepsilon a\left\{1+{\frac {1}{2D}}+{\frac {1}{4D^{2}}}+{\frac {1}{8D^{3}}}+{\frac {1}{8D^{4}}}+{\frac {3}{32D^{5}}}+{\mathcal {O}}\left({\frac {1}{D^{6}}}\right)\right\}$ $=2\pi \varepsilon a\left\{\ln 2+\gamma -{\frac {1}{2}}\ln \left(2D-2\right)+{\mathcal {O}}\left(2D-2\right)\right\}$	: distance between spheres, $d>2a$ : $d/2a>1$ $\gamma$ : Euler-Mascheroni constant
Circular diskagainst infinity	$C=8\varepsilon a$	: radius
Straight wire piece (long cylinder) towards infinity	$C={\frac {2\pi \varepsilon l}{\Lambda }}\left\{1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left[1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right]+{\mathcal {O}}\left({\frac {1}{\Lambda ^{3}}}\right)\right\}$	: length : wire radius $\Lambda$ : $\ln(l/a)$

Here, if necessary, A denotes the area of the electrodes, d their distance, l their length, $R_{1}$ as well as $R_{2}$ their radii and ε $\varepsilon$ the permittivity (dielectric conductivity) of the dielectric. It is ε $\varepsilon = \varepsilon_0 \varepsilon_\mathrm{r}$ , where ε $\varepsilon _{0}$ is the electric field constant and ε $\varepsilon _{\mathrm {r} }$ is the relative permittivity. In the schematic diagram, the conductors are colored light gray and dark gray, respectively, and the dielectric is colored blue.

Capacity calculations

The following general equations for the determination of the capacitance apply to the respective time-dependent quantities current i(t) , voltage u(t) and charge q(t) at a constant electrical capacitance :

$i(t)={\frac {\mathrm {d} q(t)}{\mathrm {d} t}}=C\cdot {\frac {\mathrm {d} u(t)}{\mathrm {d} t}}$

$u(t) = \frac{1}{C} \cdot \int i(t) \, \mathrm dt$

An expression for the capacitance of any electrode array or charge distribution can be derived using Gauss's theorem:

$C = \frac{Q}{U} =\frac{ \oint_{A} \vec D \cdot \mathrm d \vec{A}} {\int_s \vec E \cdot \mathrm d \vec {s}}$

Here, the dielectric shift ${\vec {D}}=\varepsilon _{0}\cdot \varepsilon _{\mathrm {r} }\cdot {\vec {E}}$ , thus:

$C=\varepsilon _{0}\cdot \varepsilon _{\mathrm {r} }\cdot {\frac {\oint _{A}{\vec {E}}\cdot \mathrm {d} {\vec {A}}}{\int _{s}{\vec {E}}\cdot \mathrm {d} {\vec {s}}}}$

For a vacuum, this equation simplifies to because of ε $\varepsilon _{r}=1$

$C = \varepsilon_0 \cdot \frac{ \oint_{A} \vec E \cdot \mathrm d \vec A }{\int_s \vec E \cdot \mathrm d \vec s}$

A calculation of the capacitance requires knowledge of the electric field. For this purpose, the Laplace equation $\nabla^2\varphi=0$ with a constant potential φ $\varphi$ on the conductor surfaces must be solved. In more complicated cases, no closed form of the solution exists.

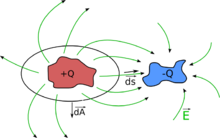
General situation for capacity determination

Measure capacity

The measurement of capacitance is not only used to control the capacitance of a capacitor (component), but is also used, for example, in capacitive distance sensors to determine the distance. Other sensors (pressure, humidity, gases) are also often based on a capacitance measurement.

According to the above relationships, the capacity can be determined as follows:

Charging with constant current and observing the rate of voltage rise
Measuring the resonant frequency of an LC resonant circuit formed with the capacitance.
Applying an AC voltage and measuring the current waveform

In particular, the latter method is used in capacitance measuring devices, where not only the magnitude of the current but also its phase relation to the voltage is recorded. In this way, the impedance and the loss angle or quality factor of the capacitor can also be determined.