Boson
This article has been entered into the Physics Editor's Quality Assurance. If you are familiar with the topic, you are welcome to participate in reviewing and possibly improving the article. The exchange of views on this is currently not on the article discussion page, but on the physics quality assurance page.
The title of this article is ambiguous. For the Swedish handball player see Matilda Boson
Bosons (after the Indian physicist Satyendranath Bose) are all particles that behave according to Bose-Einstein statistics, in which, among other things, several indistinguishable particles can occupy the same state. According to the spin-statistics theorem, they have an integer intrinsic angular momentum (spin) in units of Planck's reduced quantum of action 
. This is how they can be distinguished from fermions with half-integer spin and anyons with arbitrary (even fractional) spin; both types have different statistical properties.
In the Standard Model of particle physics, the exchange particles that mediate the forces between the fermions are elementary bosons with a spin of 1, such as the photon as the transmitter of the electromagnetic force. The hypothetical graviton as the carrier of gravitation is also a boson, but with a spin of 2. Furthermore, with the Higgs boson, a boson with a spin of 0 exists in the Standard Model.
Other bosons are composed of several particles, such as the Cooper pairs of electrons and phonons as charge carriers in the superconductor, atomic nuclei with an even number of nucleons, or the mesons, i.e. subatomic quark-antiquark pairs. Furthermore, also quasiparticles can show bosonic properties, like the already mentioned phonons or the spinons.
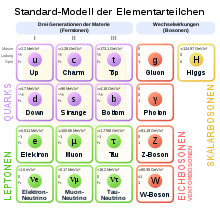
Standard model with the gauge bosons (red) and the scalar bosons (yellow)
Classification according to spin
The elementary bosons are designated differently depending on their spin. The basis of this designation is their transformation behaviour under the "actual orthochronous Lorentz transformations". Elementary particles can have at most a spin of 2, except in a non-local or a string theory, because massless particles are subject to the low-energy theorem, which excludes the coupling of high spins to currents of other spins, as well as a prohibition on self-interactions, and for massive particles the general non-existence was shown in 2017. Bosons with higher spin are therefore physically less relevant, since they only appear as composite particles.
| Spin | Boson type | Representative | |
| elementary | Composite | ||
| 0 | Scalar Boson | Higgs boson | Pions, 4He core |
| 1 | Vector boson | Photon, W-boson, Z-boson, gluon | J/ψ meson, 14N core |
| 2 | Tensor boson | Graviton (hypothetical) | 36Cl core, 60Co core |
| 3 | - – | - – | 10B core |
Macroscopic quantum states
A special property of bosons is that when two identical bosons are swapped, the quantum mechanical wave function does not change (phase factor +1). In contrast, when two identical fermions are interchanged, the sign of the wave function changes. The reason for the invariance of the wave function in the case of boson interchanges is given by the relatively complicated spin statistics theorem. Clearly, after two permutations (i.e. a mirroring or application of the parity operator), the original state is obtained again; a one-time permutation can therefore only produce a factor of the magnitude 1, which squares to 1 - i.e. either 1 or -1 -, where the 1 corresponds to the bosons.
One consequence is that bosons of the same kind can be in the same place at the same time (within the uncertainty principle); this is called a Bose-Einstein condensate. Several bosons then occupy the same quantum state; they form macroscopic quantum states. Examples are:
- superconductivity described by bosonic Cooper pairs,
- the laser in which photons assume the same state,
- the superfluidity, where bosonic 4He or 6Li condense, or bosonic pairs of fermionic 3He.
