Adder (electronics)

A full adder is a switching network that is usually realised as a digital circuit. It consists of three inputs ( , and $c_{\mathrm {in} }$ ) and two outputs ( and $c_{\mathrm {out} }$ ). A full adder can be used to add three one-digit binary numbers. The output (sum) is the lower digit of the result, the output $c_{\mathrm {out} }$ (carry (output)) is the higher digit. The identifiers $c_{\mathrm {in} }$ and $c_{\mathrm {out} }$ suggest a possibility for carry treatment in adder networks.

The following truth table shows how a full adder works:

This results in the following equations by first forming the disjunctive normal form from the truth values of the table and then simplifying:

${\begin{aligned}c_{\mathrm {out} }&=\left({\overline {x}}\wedge y\wedge c_{\mathrm {in} }\right)\vee \left(x\wedge {\overline {y}}\wedge c_{\mathrm {in} }\right)\vee \left(x\wedge y\wedge {\overline {c_{\mathrm {in} }}}\right)\vee \left(x\wedge y\wedge c_{\mathrm {in} }\right)\\&=(c_{\mathrm {in} }\wedge (x\oplus y))\vee \left(x\wedge y\right)\end{aligned}}$

and

$s=x\oplus y\oplus c_{\mathrm {in} }$

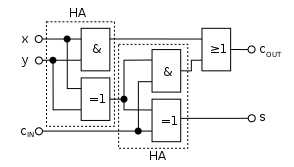
The illustration on the left shows the construction of a full adder using half adders and an Oder gate.

The figure on the right also shows the structure of a full adder, whereby the half adders have each been separated into an AND gate and an exclusive OR gate. Note that in both figures the sum outputs shown at the bottom and the carry outputs of the half adders $c_{\mathrm {out} }$ shown at the top.

Further optimising the expression for the full adder without slowing down the carry path results in further simplifications:

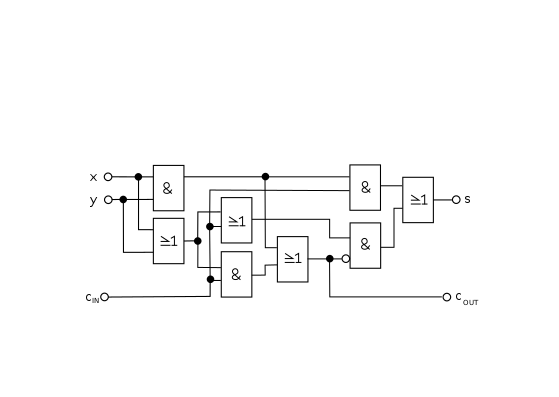
Fulladder without XOR for TTL

${\begin{aligned}I&=x\wedge y\\J&=x\vee y\\c_{out}&=I\vee (x\wedge c_{in})\vee (y\wedge c_{in})\\c_{out}&=I\vee ((x\vee y)\wedge c_{in})\\c_{out}&=I\vee (J\wedge c_{in})\\s&=(x\wedge {\overline {c_{out}}})\vee (y\wedge {\overline {c_{out}}})\vee (c_{in}\wedge {\overline {c_{out}}})\vee (I\wedge c_{in})\\s&=((J\vee c_{in})\wedge {\overline {c_{out}}})\vee (I\wedge c_{in})\end{aligned}}$

The full adder is used to build adders and multipliers, often with a half adder at the beginning of the carry chain.

Circuit symbol of a full adder

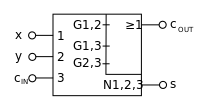
Switching symbol of a full adder according to DIN 40900

Structure of a full adder with two AND, two XOR and one OR gates according to DIN 40900

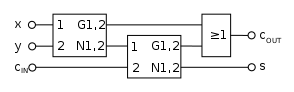
Construction of a full adder by means of two half adders and an Oder gate according to DIN 40900

Adder (electronics)

Search by letter