0

The number zero is the number of elements in an empty collection of objects, mathematically speaking the cardinality of the empty set. In mathematics, zero denotes objects defined in different ways depending on the context, but which can often be identified with each other, i.e. considered as the same object combining different properties compatible with each other. Since cardinal numbers (number of elements of a set) are identified with special ordinal numbers, and zero is just the smallest cardinal number, zero is also chosen as the first ordinal number - contrary to common usage. As a finite cardinal and ordinal number, it is also counted among the natural numbers, depending on the definition. Zero is the neutral element with respect to addition (vividly, the difference of two equal numbers) in many bodies, such as the rational numbers, real numbers, and complex numbers, and a common name for a neutral element in many algebraic structures, even when other elements are not identified with common numbers. As an integer, zero is successor to minus one and predecessor to one. On a number line, zero separates the positive numbers from the negative numbers. Zero is the only real number that is neither positive nor negative. The number zero is even.

Zero is represented by the digit "0", whose introduction made place value systems such as decimal numbers possible in the first place.

The story of the zero

It was not until the invention of a place value system with the gap sign "0" and the consideration of "0" as a digit in its own right, representing something that could be calculated with in the same way as other numbers, that the idea that zero "0" was a number was born. This laid a foundation for the further development of mathematics.

Old World

Babylonia

In the Persian (539-331 BC) and mainly the Seleucid (305-63 BC) periods, there was a misplaced sign in the Babylonian sexagesimal system as a precursor to the number zero, namely in sexagesimal numbers in places of no value. Before that, it was only used in Old Babylonian times (around 1800-around 1500 BC) in some texts to avoid ambiguities like sexagesimal 30.16 (= 30×60 + 16 = 1816) and 20.26 (= 20×60 + 26 = 1226) or 10.36 (= 10×60 + 36 = 636), a place without value was then represented by a gap. In most cases, however, it was necessary to infer the absence of digits from the context, but this was very seldom necessary, for in the extant texts only about a dozen such cases are found among thousands of numerical entries. The sexagesimal numbers of the Babylonians had no fixed order of magnitude; for example, decimal 123 (= 2×60 + 3) was written exactly as 7380 (= 2×60² + 3×60) or 2.05 (= 2 + 3/60). Only in astronomical texts this changed from 200 BC on and the misspelled sign was used there also at the end of numbers.

Already in old-Babylonian time there were differences in algebraic texts for intermediate results, which also became zero. In such cases, however, the texts only stated that minuend and subtrahend were equal, there is neither a name for zero nor was a number zero recognized as a solution to algebraic tasks. The Babylonians therefore did not yet know the number zero.

Egypt, Greece and Roman Empire

In Egypt, in the 2nd century BC, an inscription was placed on the temple of Horus in Edfu, in which the dimensions of temple lands are given. The lands were divided - according to today's interpretation, which is not certain - into quadrilateral and triangular plots, the areas of which were then approximately calculated from the four side lengths according to a general formula for quadrilaterals. In the case of triangles, the fourth side was set to zero and the hieroglyph was used to indicate this ("nothing") is used. The number zero was therefore perhaps already known at this time in Egypt.

The Greeks, on the other hand, did not know the number zero. Only the Hellenistic world took over from the Babylonians with astronomy also their sexagesimal fractions, but these were written with the Ionic number symbols. This was also the case with the Greek astronomer Klaudios Ptolemaios, who worked in the famous library of the Museion in Alexandria in the 2nd century AD. He used the misspelled o in astronomical indications, which probably stands for Greek οὐδέν ouden ("nothing").

Although the Roman emperors promoted the sciences in the former Hellenistic regions of their empire, the Romans had no significant mathematical achievements of their own to show. There was no sign for the zero in Latin.

India and Southeast Asia

Probably influenced by the Babylonian sexagesimal system as well as astronomy and calendar calculation, the decimal place value system with 0 and numeral signs for 1, ..., 9 developed in India between 300 B.C. and 600 A.D., which had apparently originated from own numeral signs that existed for Indian scripts. Since in decimal numbers places with a gap, i.e. the value zero, occur much more frequently than in the Babylonian sexagesimal system, a gap sign for zero became indispensable in the decimal place value system, which must have been conducive to the acceptance of zero as a number. According to radiocarbon dating published in 2017, the oldest material evidence for a written symbol of zero in Indian space is found in the Bakhshali manuscript. According to this, the oldest parts of the manuscript date back to the 3rd or 4th century A.D. The interpretation of the results of the radiocarbon dating that has become widespread among the public in the process has been questioned by other researchers such as Kim Plofker. According to them, the manuscript shows a uniformity in both writing, content and state of preservation that suggests it should be assigned to the latest date of dating.

Since the 7th century AD, a dot or a circle is found in inscriptions as a symbol for the "void" ("śūnya"), as zero was called in India at least since the 5th century AD. In his textbook "Brāhmasphutasiddhānta" written in 628 AD, the mathematician and astronomer Brahmagupta, who taught in Bhinmal (Rajasthan), gave calculation rules for zero as well. An earlier confirmed evidence of zero as a number in India (even earlier in Southeast Asia) is a stone tablet from the village of Gwalior 500 km south of New Delhi with the dates December 27, 786, January 10, 787, and January 17, 787, which is about a garden whose length is 270 (hastas) and received 50 garlands of flowers.

Another early written use of the zero is found in inscription K. 151 from Sambor Prei Kuk in Cambodia, dating from the beginning of the 7th century AD, and reporting the erection of a statue of a god on 14 April 598: The year of the Śaka era used here is 520, with the zero rendered as "airspace" ("kha"). Another record of the use of the numeral "0" also comes from Cambodia, in inscription K. 127, where the Śaka year "605" is mentioned in numerals, corresponding to our year 683/84. A whole series of inscriptions whose date contains "0" and which date from about the same time have been found on Sumatra.

In the original Indian systems, the order of the powers was reversed, the ones were called first, then the tens, etc. The digit zero thus increased the value of the following digit.

China

In ancient China, no number zero was known, because problems never had a number zero as a solution and there was no independent zero with which one could calculate as with other numbers. Numbers, however, were probably interpreted by rods at least since the 1st century AD (early Han dynasty) (Jiu Zhang Suanshu, Chapter 8, Problem 3): The ones vertically, the tens horizontally, the hundreds vertically again, etc., whereby at a place with more than 5 rods, 5 of them were replaced by a rod in the other direction. Thus one had a decimal place value system, in which however - as in the original sexagesimal system of the Babylonians - there was no missing sign for places without value. It is only in the translation of an Indian astronomical text from the time between 713 and 741 A.D. that the earliest known Chinese mention of a missing sign (a dot) is found.

Likewise, a kind of matrix calculation for solving systems of linear equations was probably already known in the 1st century AD (Jiu Zhang Suanshu, chapter 8). Negative values also appeared in the calculations, which were represented with rods - for the first time in history - differently from positive values. For these, addition and subtraction rules were given, in particular also for empty entries corresponding to matrix elements with the value zero. Thus one had a computational precursor to the number zero. The sign rules of multiplication, on the other hand, are not attested in China until 1299 AD.

Europe from the Middle Ages

While large parts of Western Europe suffered from the disintegration of the Roman Empire and other factors, especially in the early Middle Ages, mathematics continued to be practiced at a high level in Byzantium (University of Constantinople) and in the now Islamicized areas by Muslims, Jews and Christians. Indian numerals with their decimal system were first described by the Syrian bishop and scholar Severus Sebokht in the 7th century, and spread over a wide area with the work On Arithmetic with Indian Numerals (c. 825) by al-Chwarizmi, a Khorezmian mathematician. Other arithmetic books, such as those by Ibn Ezra in the 12th century, followed.

Leonardo Fibonacci, a mathematician of the Middle Ages who, as the son of an Italian merchant in Algiers, was familiar with Arabic-Indian numbers, including zero, introduced them to Italy in 1202 with his work Liber abaci, in which he worked on examples from the world of commerce. However, he did not give zero the same status as the other numbers - in his book he calls it a sign instead of a number. The use of zero in practical arithmetic, however, did not become established until much later (in the 17th century). Even Gerolamo Cardano in the 16th century managed without it.

For the digit and the "new number" 0, many European languages have a different name from the German word "null"; for these differences, see below under Origin of the word.

In the following centuries, the zero gained importance in many areas. The zero became the starting point for many scales, for example, temperature or sea level, and so the concepts of "positive" and "negative" grew in people's minds.

Falsely, it is also repeatedly claimed that it was Pope Sylvester II. (with civil name Gerbert of Aurillac) was the one who brought the Arabic-Indian numbers to Europe.

New World

Olmec and Maya

The Olmecs were the first people in Mesoamerica to develop a first form of astronomical calendar. The earliest date in this calendar discovered so far is 7.16.6.16.18 and probably corresponds to a day in September 32 BC (Long Count). The Maya also had such a calendar, from which they developed a pure number representation in the Vigesimal system (place value system to the base 20). Digits with the value zero were symbolized by a shell or a snail shell. The oldest date found so far shows a day in the year 36 BC.

Inca

A decimal place value system has been proven for the Inca people: They used the knot script of the Quipus, which was based on such a system. A place on the thread without a knot served as a misplaced character.

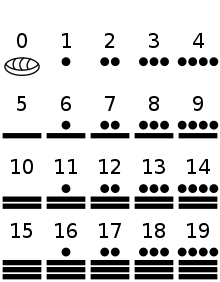
The number symbols of the Maya. The number zero was represented by a sign resembling a shell or a snail shell.

Symbols and notations

The Indian digit 0

If there is a risk of confusion with the capital Latin letter O, the digit 0 is marked with a slash or dot, e.g.: or or .

In mathematics, the symbol "0" often stands for zero elements of structures in general, even if they are distinguished from a number 0.

Other payment fonts

• Chinese zero

The zero in the place value system

A single digit 0 denotes the number zero, otherwise a digit 0 in a position means that the corresponding place value representation of a number does not occur, e.g. "307" for 3-100 + 0-10 + 7-1. If the digit 0 is appended to a sequence of digits, its value is multiplied by the base of the place value system.

Leading zeros are usually omitted or replaced by spaces in formatted output.

For decimal numbers, zeros after the decimal point are usually omitted if they are not followed by another digit. In a formatted output, they are written according to the output format. An exception is the specification of measured values. Here, the zero is often written additionally to illustrate the accuracy of the measurement.

Example: A length is measured with 1.200 m. The two additional zeros here show that the measurement was accurate to three decimal places.

Type specifications are often made with leading zeros, e.g. 001. Also in the case of numbering, such as order numbers, invoice numbers, ID card numbers and so on, whose sequence of digits is fixed to a certain number of digits, unused digits are filled with leading zeros at the beginning.