Work (thermodynamics)

This article deals with closed systems, i.e. in particular a constant amount of substance (subject to chemical reactions); for flowing systems see hydraulics.

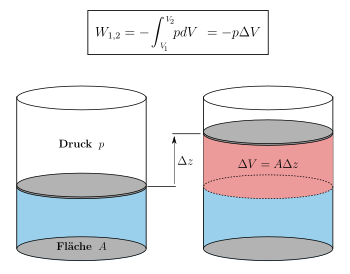
The volume work or volume change work is the work to be done on a closed system to change the volume of the system from the value V_1 to one with the value V_2

when the volume is reduced $(V_{2}<V_{1})$ compression, compression work is done, i.e. supplied to the system (in the figure this is the work done by the piston on the gas contained in the cylinder):
when the volume increases $(V_{2}>V_{1})$ expansion, work - i.e. energy - is released, i.e. given off by the system:

The formula for the volume work is:

$W_{1,2}=-\int \limits _{s}F(s)\cdot \mathrm {d} s$ .

Here F(s) the force acting along a path ; this is counted positively in the direction of expansion (in the figure opposite the compression force F_p ).

The minus sign in the formula is a convention; in this way it is achieved that work supplied to the system is positive as described above, while energy released is given a negative sign. In the compression shown, the distance travelled has a negative sign which $\left({\mathrm {d}}s<0\right),$ is compensated for by the additional minus sign in the formula for the volume work.

When a piston expands by a distance Δ $\Delta z$ against an external pressure , it does the volume work $W_{\rm {1,2}}$ .

Smooth process

The work supplied frictionlessly and quasistatically is in the cylinder shown with cross-section $\left(\Rightarrow {\mathrm {d}}s={\frac {{\mathrm {d}}V}{A}}\right)$

because $F=p\cdot A$ (freedom from friction):

$\Rightarrow W_{\mathrm {1,2} }=\int \limits _{V_{1}}^{V_{2}}\delta W=-\int \limits _{V_{1}}^{V_{2}}p\cdot \mathrm {d} V$

with

$\delta W=-pdV$ the inexact differential of the volume work
: Pressure
$\mathrm {d} V$ : volume change.

In the p-V diagram, this change of state runs from point 1 to point 2, i.e. in the case of the compression shown in the negative volume direction without the minus sign in the formula, the compression work would have a negative sign. $\left({\mathrm {d}}V<0\right);$

The integral value, which corresponds to the area under the state curve, can be calculated if the function p = f(V) is known (see below).

Frictional process

In the real case, if a frictional force acts between the piston and the cylinder, the frictional work must be $W_{R}$ applied in addition to the volume change work during compression. This increases the internal energy of the system and thus the pressure compared to the frictionless process (if it is not dissipated to the outside as heat by cooling):

${p_{2}}'>p_{2}$

In the p-V diagram, the change of state now runs from point 1 to point 2'. This means that the work of change in volume, which corresponds to the area under the curve, also becomes greater, without the friction work itself being included in it:

$\Rightarrow W_{{1,2'}}>W_{{1,2}}$

The work to be done from the outside is therefore the sum of the now greater volume change work and the friction work:

$W_{{{\mathrm {ext}}}}=W_{{1,2'}}+W_{R}$

Calculation example

Assume the isothermal expansion of an ideal gas $\left(T={\text{konst.}}\right).$

Then, by substituting the thermal equation of state of ideal gases:

$p(V)=n\cdot R\cdot T\cdot {\frac {1}{V}}$

with

n is the amount of substance
R is the general gas constant
T the absolute temperature

solve the integral for the volume work:

${\begin{aligned}\Rightarrow W_{{\mathrm {1,2}}}&=-&n\cdot R\cdot T\cdot \ln {\frac {V_{2}}{V_{1}}}\\&=&n\cdot R\cdot T\cdot \ln {\frac {V_{1}}{V_{2}}}\end{aligned}}$

Using this equation, we see that during the expansion of an ideal gas, the volume work is negative, i.e. energy is released; this follows from the logarithm, which is negative for numbers less than one and positive for numbers greater than one:

${\begin{aligned}V_{2}>V_{1}\\\Leftrightarrow {\frac {V_{2}}{V_{1}}}>1\\\Leftrightarrow \ln {\frac {V_{2}}{V_{1}}}>0\\\Rightarrow W_{{\mathrm {1,2}}}<0\end{aligned}}$

Instead of n-R, one can also insert m-Rs above:

$n\cdot R=m\cdot R_{{\mathrm {s}}}$

where

m is the mass of the substance and
_{Rs is} its specific gas constant.

Open system

If the compression is carried out in an open system with the external pressure $p_{0}$ , the actual work to be done is as follows

$W_{1,2}=p_{0}\cdot (V_{2}-V_{1})$

since the external pressure multiplied by the surface area also results in a force. If the external pressure is higher than the internal pressure of the volume to be compressed, energy is gained; if it is lower, work must be done.