Vorticity

The vorticity ω ${\vec {\omega }}$ or η ${\vec {\eta }}$ or ${\vec {\zeta }}$ quantifies a central quantity of fluid mechanics and meteorology by assigning a field of velocities to the vortex and circular or spiral flows. The equivalent term vorticity from Latin vortex = "vortex, whirlpool", English vorticity, is translated as vorticity.

In fluid mechanics, small differences in velocity and direction of gases and liquids are called shear. On the other hand, streamlines are geometric aids for the descriptive description of a flow as a directed movement of particles. Finally, viscosity is the viscosity of fluids, i.e. the resistance of the fluid to shear.

The vorticity corresponds to the tendency of a fluid element to self-rotate about an axis, which results in a circulation of flowing or flowing media in a closed area. Furthermore, the mean of the square vorticity over a certain area is called enstrophy, which describes, for example, the flow behaviour of glass double facades.

Formal notation

The vorticity ω ${\vec {\omega }}$ , ${\vec {\zeta }}$ denoted in meteorology by circulation, is defined as the rotation of velocity ${\vec {u}}$ a vector field:

${\vec {\omega }}:=\operatorname {rot} {\vec {u}}={\vec {\nabla }}\times {\vec {u}}$

It has the SI unit ${\tfrac {1}{\mathrm {s} }}$ and, like any rotation of a vector field, is a pseudovector field.

Because a closed system does not change the conservation variables, the vorticity is equal to the areal circulation rate Γ $\Gamma$ :

$\Gamma :=\oint _{\partial A}{\vec {v}}\cdot \mathrm {d} {\vec {r}}=\int _{A}\;\operatorname {rot} ({\vec {v}})\cdot \mathrm {d} {\vec {A}}$

$\Rightarrow {\vec {\omega }}\cdot {\vec {n}}={\frac {\mathrm {d} \Gamma }{\mathrm {d} A}}$

with normal ${\vec {n}}$ .

In meteorology, except for true three-dimensional vortices such as tornadoes, two-dimensional velocity fields are often present. The corresponding vorticity points in the z-direction and is as follows

${\vec {\zeta }}:=\operatorname {rot} {\vec {u}}_{2D}=\left({\frac {\partial u_{y}}{\partial x}}-{\frac {\partial u_{x}}{\partial y}}\right){\vec {e}}_{z}$ .

Hydrodynamics

In hydrodynamics, vorticity is the rotation of the fluid velocity oriented in the direction of the axis of rotation, or perpendicular to the plane of flow for two-dimensional flows. For fluids with a fixed rotation about an axis (e.g. a rotating cylinder), the vorticity is equal to twice the angular velocity ω0 of the fluid element:

${\vec {\omega }}=2{\vec {\omega }}_{0}$

${\vec {\omega }}={\vec {\nabla }}\times {\vec {u}}={\vec {\nabla }}\times \left({\vec {\omega }}_{0}\times {\vec {r}}\right)={\vec {\omega }}_{0}\left({\vec {\nabla }}\cdot {\vec {r}}\right)-\left({\vec {\omega }}_{0}\cdot {\vec {\nabla }}\right){\vec {r}}=3{\vec {\omega }}_{0}-{\vec {\omega }}_{0}=2{\vec {\omega }}_{0}$

Fluids without vorticity are called rotation- or vortex-free with ω ${\vec {\omega }}=0\;{\text{bzw.}}\;\zeta =0$ . However, the fluid elements of such a rotation-free fluid can also ${\vec {\omega }}_{0}\neq 0$ have an angular velocity ω , i.e. move on curved paths, cf. the following figure, where the letter ω $\omega$ in the text stands for the vorticity and in the figure for the angular velocity:

Consider an infinitesimally small, square region of a fluid. When this region is rotating, the vorticity of the flow is nonzero. The vorticity refers to forced vortices with ω ${\vec {\omega }}=\operatorname {rot} {\vec {u}}\neq 0$ .

Vorticity is a suitable means for fluids with small viscosity. Then the vorticity can be considered equal to zero at almost all locations of the flow. This is obvious for two-dimensional flows where the flow can be represented on the complex plane. Such problems can usually be solved analytically.

For any flow, the governing equations can be related to vorticity instead of velocity by simple substitution. This leads to the vortex density equation, which for incompressible, inviscid fluids is as follows:

${\frac {\mathrm {D} {\vec {\omega }}}{\mathrm {D} t}}=({\vec {\omega }}\cdot {\vec {\nabla }}){\vec {u}}$

Even for real flows (three-dimensional, finite Reynolds number, i.e. non-zero viscosity), the consideration of the flow via the vorticity can be used with restrictions, if one assumes that the vorticity field can be represented as an arrangement of individual vortices. The diffusion of these vortices through the flow is described by the vortex transport equation:

${\frac {\mathrm {D} {\vec {\omega }}}{\mathrm {D} t}}=({\vec {\omega }}\cdot {\vec {\nabla }}){\vec {u}}+{\frac {\eta }{\rho }}\cdot (\nabla ^{2}{\vec {\omega }})$

where $\nabla ^{2}$ denotes the Laplace operator. Here, the vortex density equation has been ${\frac {\eta }{\rho }}\cdot (\nabla ^{2}{\vec {\omega }})$ augmented by the diffusion term η

For highly viscous flows, for example Couette flows, it may be more appropriate to consider directly the velocity field of the fluid instead of the vorticity, since the high viscosity leads to a very strong diffusion of the vortices.

The vortex line is directly related to the vorticity in that vortex lines are tangents to the vorticity. The set of vortex lines passing through an area element is called the vortex filament. Helmholtz's vortex theorems state that the vortex flux $\iint {\vec {\omega }}\cdot \mathrm {d} {\vec {A}}$ is constant in both time and space.

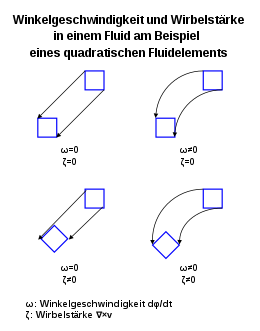
Vorticity and angular velocity

Questions and Answers

Q: What is vorticity?

A: Vorticity is a mathematical concept used in fluid dynamics which relates to the amount of "circulation" or "rotation" (or more strictly, the local angular rate of rotation) in a fluid.

Q: How is vorticity calculated?

A: The average vorticity in a small region of fluid flow is equal to the circulation around the boundary of the small region, divided by the area A of the small region. Mathematically, it can also be defined as the curl of velocity at a point.

Q: Is there any base assumption related to vorticity?

A: Yes, one of the base assumptions of potential flow assumption is that vorticity is zero almost everywhere, except in a boundary layer or stream-surface immediately bounding a boundary layer.

Q: What happens when there are regions with non-zero vorticity?

A: These regions can be modelled with vortices because they are regions with concentrated vorticity.

Q: What does Γ represent?

A: Γ represents circulation around a small region.

Q: What does ω represent?

A: ω represents average vorticity in a small region and also represents vector and curl of velocity at a point.