Voltage

The electric voltage (often simplified as voltage) is a fundamental physical quantity of electrical engineering and electrodynamics. Its formula symbol is the . It is specified in the international system of units in the unit volt (unit symbol: V). To indicate a time dependence, the lower case letter is used for the instantaneous value of the voltage. In Anglo-Saxon, the formula symbol is used.

Put simply - and appropriately in everyday electrical circuits - voltage characterizes the "strength" of a voltage source; it is the cause of the electric current that carries the electric charge. For example, when the two poles of a battery or a power outlet are connected by an electrically conductive component, current flows. The magnitude of the electric current depends on the magnitude of the voltage and on a property of the conductive component called electrical resistance. In the opposite way of looking at it, a voltage occurs across a body through which current flows, which is then called voltage drop. According to the electro-hydraulic analogy, the voltage that drives the electric charge through the conductor can be thought of as the difference in pressure between two points in a pipe that drives the fluid through the pipe.

According to basic physics, voltage expresses the ability to move charges so that a current flows through the connected load and work is performed. The electric voltage between two points is defined as the line integral of the electric field strength along a fixed path from one point to the other. It is also the difference in potential electrical energy that a charge has at the two points, relative to that charge. This is also simplified as "voltage = energy per charge".

In a "natural" way, electrical voltage is generated, for example, by friction, during the formation of thunderstorms, by ion transport through a biomembrane and during chemical redox reactions. For technical use, voltages are mostly generated by electromagnetic induction as well as by processes of electrochemistry.

Electrical voltages exist in a wide range of magnitudes. They can cause life-threatening currents for humans.

Alessandro Volta, physicist and eponym of the unit of tension

Electrical potential

→ Main article: Electrical potential

Formula symbols for the electric potential are and φ $\varphi$ . This potential at a point P in space is ${\vec {A}}$ defined by means of the electric field strength ${\vec {E}}$ and the magnetic vector potential by

$-{\vec {\nabla }}V={\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}$

with the remark: The electric potential is not unique, because any constant scalar quantity can be added to a given potential without changing its gradient.

For uniqueness, a reference point P0 is established which receives zero potential $V_{\mathrm {P_{0}} }=0$ . There are conventions for choosing the reference point in many fields, so it is often not mentioned linguistically. In electrical engineering, the reference point is placed on that part of the conductor that is labeled "ground"; in electric field theory, the reference point is often placed "at infinity".

The integral value with respect to the reference point P0 is called the electric potential.

$V=-\int _{\mathrm {P_{0}} }^{\mathrm {P} }\left({\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}\right)\cdot \mathrm {d} {\vec {s}}$ .

With the potentials $V_{\mathrm {A} }$ and $V_{\mathrm {B} }$ at points A and B, the definition of the voltage gives

$U_{\mathrm {AB} }=\int _{\mathrm {A} }^{\mathrm {B} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}=-(V_{\mathrm {B} }-V_{\mathrm {A} })-\int _{\mathrm {A} }^{\mathrm {B} }{\frac {\partial {\vec {A}}}{\partial t}}\cdot \mathrm {d} {\vec {s}}$ .

In a potential field, ∂ ${\frac {\partial {\vec {A}}}{\partial t}}=0$ . In the following, we will assume only the electric voltage in a potential field. There apply

$V_{A}=-\int _{\mathrm {P_{0}} }^{\mathrm {A} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}=\int _{\mathrm {A} }^{\mathrm {P_{0}} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}\quad ;\qquad V_{B}=\int _{\mathrm {B} }^{\mathrm {P_{0}} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}$

$U_{\mathrm {AB} }=V_{\mathrm {A} }-V_{\mathrm {B} }$ .

The electric voltage between these locations is therefore equal to the difference of the electric potentials at these locations.

The specification of a voltage at one point is only possible in exceptional cases if the second point for the voltage is known from the circumstances; otherwise the voltage can always only be specified between two points. In contrast, the potential depends only on the selected point in space and can therefore be specified as a location-dependent function. It thus represents a scalar field which (except for one constant) can be determined from the electric field and, conversely, uniquely determines the electric field.

Positive charge carriers move - if no further forces act on them - in the direction of the field strength. Because they lose potential energy in the process, the electric potential decreases in this direction. Negatively charged objects, on the other hand, move against the field strength in the absence of other forces, in the direction of increasing potential.

For a shift along an equipotential line, the integral is zero because on this path ${\vec {E}}\perp \mathrm {d} {\vec {s}}$ , so the scalar product is zero.

If a charge is transported from A to B and via any other path back to A, the ring integral over the closed circuit disappears in the potential field:

$\oint {\vec {E}}\cdot \mathrm {d} {\vec {s}}=0$

Electrical voltage measurement

→ Main article: Voltmeter

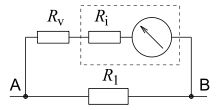
The voltmeter used to measure a voltage is connected in parallel with the object whose voltage is to be measured.

When using a moving-coil movement, which by its physics is a current measuring device, a current divider circuit is created for voltage measurement. The current is measured by the internal resistance $R_{{\text{i}}}$ of the measuring device as a measure of the voltage. Since each measuring device has a limited measuring range, the current must be reduced via a series resistor if the maximum measurable value is exceeded, $R_{\text{v}}$ thus extending the measuring range.

The measurement error caused by the current branching (the feedback error due to the measuring device) is kept small if $R_{\text{i}}+R_{\text{v}}$ is $R_{1}$ large compared to the DUT This is because it is the only way that the total resistance of the measuring circuit remains approximately unchanged, and the measuring circuit has negligible influence on the rest of the circuit. For the comparison, the factor is introduced here

$R_{\text{i}}+R_{\text{v}}=x\cdot R_{1}\ .$

In a parallel circuit, the currents in the parallel branches add up to the total current and the conductances of the branches add up to the total conductance.

${\frac {1}{R_{\mathrm {ges} }}}={\frac {1}{R_{1}}}+{\frac {1}{R_{\text{i}}+R_{\text{v}}}}$

and using this results in

${\frac {1}{R_{\mathrm {ges} }}}={\frac {1}{R_{1}}}+{\frac {1}{x\cdot R_{1}}}\quad \Rightarrow R_{\mathrm {ges} }={\frac {x}{x+1}}\cdot R_{1}\ .$

If the term relative measurement deviation is used

$f={\frac {x_{\text{a}}-x_{\text{r}}}{x_{\text{r}}}}$

with the correct value $x_{\text{r}}$ and the value deviating from it to $x_{\text{a}}$ this circuit, the following results

$f={\frac {R_{\mathrm {ges} }-R_{1}}{R_{1}}}={\frac {x}{x+1}}-1={\frac {-1}{x+1}}\quad \Rightarrow \quad x={\frac {1}{-f}}-1\ .$

For example, if this always negative variance is required to be $|f|<1\;\%=0{,}01$ , then $x>99$ . If $R_{\text{i}}+R_{\text{v}}$ 100 times as large as $R_{1}$ , then is $R_{\mathrm {ges} }$ 1% less than . $R_{1}$

If the current from A to B comes from a constant current source, in this case the voltage is measured with a relative deviation = -1 %. If there is a constant voltage source between A and B, = 0. For any other supply, the measurement deviation is in between.

If the relative deviation that someone is willing to accept is given, the requirement for the resistance in the measurement branch is:

$R_{\text{i}}+R_{\text{v}}\geq \left({\frac {1}{|f|}}-1\right)\cdot R_{1}\ .$

With electronic voltage measuring instruments (digital measuring instrument, oscilloscope or compensation measuring recorder), the measuring range extension with a series resistor is not common; the internal resistance with these measuring instruments is typically 1 to 20 MΩ in all ranges. The series resistor would be of a magnitude that could not be reliably implemented. Instead, if the maximum measurable voltage value is exceeded, $U_{\mathrm {max} }$ a voltage divider must be used. At a tap further to the right in the adjacent circuit, a smaller voltage can be fed to the indicating part, thus increasing the full scale value $U_{\mathrm {MBE} }$ be increased.

The problem that the measuring device is connected in parallel to $R_{1}$ as above, and thus the total resistance of the measuring circuit is changed, is the same as above for the measurement with moving-coil movement. Only the series resistor of different size depending on the measuring range is $R_{\text{v}}$ omitted.

Voltage measurement at $R_{1}$ with moving-coil instrument

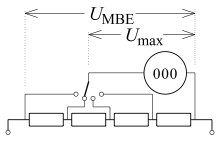
Voltage measurement with digital-electronic measuring device

Questions and Answers

Q: What is voltage?

A: Voltage is an electrical potential difference, the difference in electric potential between two places. It can be thought of as the force that pushes charges to move in a wire or other electrical conductor.

Q: What unit is used to measure voltage?

A: The unit for measuring voltage is the volt. The symbol for this unit is written with an uppercase V (9V).

Q: How does voltage cause current?

A: Voltage can cause charges to move, and since moving charges create a current, voltage can cause a current.

Q: Who was Alessandro Volta and why was the volt named after him?

A: Alessandro Volta was an Italian physicist who invented the first battery in 1800. The volt was named after him as a way of honoring his contribution to science.

Q: Are volts and voltage two different things?

A: Yes, volts are units by which we measure something while voltage refers to what we measure using those units.

Q: What are the two types of voltage?

A: There are two types of voltage - DC (direct current) and AC (alternating current). DC always has the same polarity while AC alternates between positive and negative polarities.

Q: Is it possible for birds to land on high-voltage lines without being harmed?

A:Yes, birds can land on high-voltage lines such as 12kV and 16kV without dying because there must be both voltage and current present in order for power (energy) to transfer through them - if only one element is present then nothing will happen.