Vertex (geometry)
![]()
The title of this article is ambiguous. For other meanings, see Corner (disambiguation).
The corner, also the vertex, is in geometry a particularly distinguished point of the boundary line or surface of an area.
The corners of two-dimensional polygons (polygons) are the points at which the bounding lines, the sides, meet. In the case of three-dimensional polyhedra (polyhedra), the points at which (at least) three of the bounding faces meet are called corners. The vertices of polyhedra are endpoints of the edges, i.e. the connecting lines between two adjacent vertices.
In the case of a convex n-dimensional polytope, a corner is characterized by the fact that it cannot be represented as a true convex combination of two distinct points of the polytope (extremal point).
For three-dimensional polyhedra, there is an equation that describes a relationship between the vertices, edges, and faces of any convex polyhedron, the Eulerian polyhedron theorem.
· 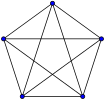
A regular pentagon has 5 corners and 5 sides.
· 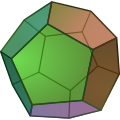
A regular dodecahedron has 12 faces (hence its name), 20 vertices, and 30 edges.
· 
A nonconvex polyhedron.
· 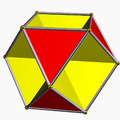
A nonconvex polyhedron with 12 vertices, 36 edges, and 32 faces for which Euler's polyhedron theorem does not hold.
Vertices in Linear Optimization
Corners play an important role in linear optimization, since it can be shown that the optimal function value is always assumed to be in a corner of the restriction set. The simplex algorithm in particular takes advantage of this by systematically running from corner to corner until it finds the optimal function value. The admissible base solutions used here are exactly the corners of the polyhedron.
Differentiation of corners
To distinguish between corners that are usually right-angled, we speak of "inside" and "outside" corners. In a convex polygon, the angles of the corners are always smaller than 180° when viewed from the inside and always larger than 180° when viewed from the outside. A corner is called an "inside corner" if its angle is less than 180°. Otherwise it is an "outside corner". Thus, in rooms, corners that you look into are inside corners and corners that protrude are outside corners. The observation is relative, that is, in relation to the object. The floor of a room lies with its outer corners in the inner corners of the room. These inner corners lie correspondingly at the outer corners of the floor.
Search within the encyclopedia