Velocity

This article explains velocity as a physical term related to a change in location. For other meanings, see Velocity (disambiguation).

Velocity, along with location and acceleration, is one of the fundamental concepts of kinematics, a branch of mechanics. The velocity describes how fast and in which direction a body or a phenomenon (for example a wave crest) changes its location in the course of time. A velocity is specified by its magnitude and the direction of motion; it is therefore a vector quantity. As a formula symbol, ${\vec {v}}$ common after the Latin or English word for speed (Latin velocitas, English velocity).

Often, the word velocity is used to refer only to its magnitude (formula character ), which, in descriptive terms, reflects the instantaneous "speed" of the movement, as displayed by the speedometer in a car, for example. distance covered by a body within a certain period of time if the velocity remains constant for a correspondingly long time. The internationally used unit is meters per second (m/s), but kilometers per hour (km/h) and - especially in maritime and aviation - knots (kn) are also commonly used.

The highest possible speed, with which the effect of a certain cause can spread spatially, is the speed of light . This upper limit is therefore also valid for any information transfer. Bodies, which possess a mass, can move only with lower velocities than

A velocity is always to be understood relative to a reference frame. If a body is at rest in one reference frame, it has the opposite velocity of the same magnitude ${\vec {v}}$ another reference frame which is moving with respect to the first one with the velocity $-{\vec v}$ .

Term history and etymology

The exact version of the everyday concepts of speed and motion was considered problematic since antiquity and throughout the Middle Ages (see, for example, "Achilles and the Tortoise" and the "Arrow Paradox"). The clarification in the physical sense comes from Galileo Galilei and marks the scientific breakthrough to modern physics at the beginning of the 17th century. Until then, only the average velocity along a given finite distance had been precisely defined, and an increase of velocity, as for example in free fall, was imagined as a sequence of small jumps of the velocity magnitude. For Galileo, however, a continuously varying velocity sweeps a continuum of all intermediate values, which he conceived not as the average velocity of a given piece of the path, but as the instantaneous velocity at the respective point of the path. The exact version of this velocity concept with the help of the boundary transition to infinitely small distances was given only at the end of the 17th century by Isaac Newton. Initially, the two aspects of magnitude and direction of velocity were treated separately until they were combined into a single mathematical quantity, the velocity vector, in the 19th century.

The word speed goes back to Middle High German geswinde ('fast, rash, impetuous, bold'), Middle Low German geswint, geswine ('strong', meaning strengthened by the prefix ge-), Middle High German swinde, swint ('mighty, strong, fierce, dexterous, quick, wicked, dangerous'). Old High German occurrence is proved by names like Amalswind, Swindbert, Swinda.

Definition

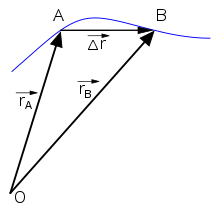
The notion of velocity (symbol ${\vec {v}}$ ) at a given point ( ) on the trajectory curve is approximated by the change in location Δ $\Delta {\vec {r}}$ in the period Δ $\Delta t$ :

${\vec {v}}_{AB}\approx {\frac {\Delta {\vec {r}}}{\Delta t}}$

Where Δ $\Delta {\vec {r}}={\vec {r}}_{B}-{\vec {r}}_{A}$ the chord of the section between points and where the body is located at the beginning and at the end of the period Δ $\Delta t$ respectively. The vector ${\vec {v}}_{AB}$ has the direction of the chord Δ $\Delta {\vec {r}}$ .

From this velocity results the instantaneous velocity at point if the point allowed to come so close to it that the quotient Δ tends towards ${\tfrac {\Delta {\vec {r}}}{\Delta t}}$ a certain value, the limit. At the same time, the time interval to zero, which is $\lim _{\Delta t\rightarrow 0}$ written as This process, called boundary transition, finds a mathematically exact basis in differential calculus. The instantaneous velocity at point is thus (in three equivalent notations):

${\vec {v}}=\lim _{\Delta t\rightarrow 0}{\frac {\Delta {\vec {r}}}{\Delta t}}={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}={\dot {\vec {r}}}$

Since the chord Δ $\Delta {\vec {r}}$ assumes the direction of the tangent to the trajectory curve at the boundary crossing, this is also the direction of the instantaneous velocity.

The magnitude of the instantaneous velocity (the "tempo" or trajectory velocity) is given by the magnitude of the velocity vector

$v=\left|{\vec {v}}\right|=\left|\lim _{\Delta t\rightarrow 0}{\frac {\Delta {\vec {r}}}{\Delta t}}\right|=\left|{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}\right|=\left|{\dot {\vec {r}}}\right|$

where $\left|{\vec {r}}\right|=r$ is the magnitude of the location vector ${\vec r}$ . The orbital velocity is not the same as $\left|{\dot {r}}\right|$ , as can be seen, for example, in circular motion with $r={\text{konst.}},\ v\neq 0,\ {\dot {r}}=0$ .

The magnitude of the instantaneous velocity can also be obtained as a scalar if only the distance (symbol ) along the trajectory is considered instead of the three-dimensional trajectory curve (see Fig.). The limit value of the quotient of the travelled distance Δ $\Delta s$ and the required time Δ $\Delta t$ is calculated:

$v=\lim _{\Delta t\rightarrow 0}{\frac {\Delta s}{\Delta t}}={\frac {\mathrm {d} s}{\mathrm {d} t}}={\dot {s}}$

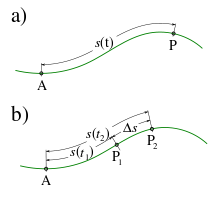
Path distances for a movement with a curved path curve

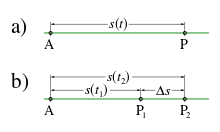
Special case of rectilinear motion

Trajectory (blue), location vectors ( ${\vec {r}}_{A}$ , ${\vec r}_{B}$ ), chord ( $\Delta {\vec {r}}$ ) and path distance (distance from to along the path curve).

Average speed

If you divide the total distance traveled by the total time elapsed to calculate the speed, the result is the average speed. The information about the change over time is lost. For example, if a car travels a distance of 100 km in one hour, it had an average speed of 100 km/h. This is the average speed of the car. It may actually have traveled at a constant speed of 100 km/h or at a speed of 200 km/h for a quarter of an hour and at a speed of 66.7 km/h for three quarters of an hour.

Note that the average speed always represents the average speed over time. If a car first drives for half an hour at a constant speed of 50 km/h and then drives for half an hour at a constant speed of 100 km/h, the average speed will be 75 km/h. However, if the car first drives a distance of 25 km at a constant speed of 50 km/h and then drives a distance of 25 km at a constant speed of 100 km/h, only half the time is required for the second movement segment (a quarter of an hour). Consequently, in this case the average speed is 66.7 km/h, although this may be counter intuitive.

Another example of bodies with variable velocity are celestial bodies whose velocities vary on elliptical orbits around a central body. In the case of Mercury, the average velocity is 47.36 km/s, but it varies between 39 and 59 km/s because of the noticeable eccentricity.

Initial velocity

If the velocity of a body or mass point at the beginning of a certain section of motion is of interest, it is also called initial velocity (formula sign usually $v_{0}$ ).

The initial velocity is one of the initial conditions when solving the equations of motion in classical mechanics, for example for numerical simulations in celestial mechanics. It is an important parameter e.g. for the trajectory in vertical and oblique throwing and for the range of firearms or rockets.

Examples:

When throwing, it is also called the dropping speed.
In external ballistics, it is identified with the muzzle velocity at which a projectile leaves the barrel of the gun.
Initial velocity of the ballistic trajectory of a missile is the firing rate.
The launch velocity of a spacecraft into an orbit or transition orbit determines its shape.
The entry velocity of objects (such as meteoroids) entering the Earth's atmosphere is essential for their further fate.

Final speed

Relationships to other physical quantities

From the temporal course of the velocity, one can infer the distance traveled by integrating over time:

$\Delta s=\int _{t_{1}}^{t_{2}}v(t)\,\mathrm {d} t$

In the simplest case, namely at constant velocity, this becomes Δ $\Delta s=v\cdot \Delta t$ .

The first derivative of velocity with respect to time is acceleration: ${\vec {a}}(t)={\dot {\vec {v}}}(t)={\ddot {\vec {s}}}(t)$ .

The second derivative of velocity with respect to time gives the jerk of a motion: ${\vec {j}}(t)={\ddot {\vec {v}}}(t)={\dot {\vec {a}}}(t)$ .

The momentum - that is, graphically speaking, the "swing" - of a body of mass calculated by ${\vec p}=m\cdot {\vec v}$ , while the kinetic energy is given by $E_{\mathrm {kin} }={\tfrac {1}{2}}mv^{2}={\tfrac {p^{2}}{2m}}$ Strictly speaking, the last two equations are only approximately valid for the so-called non-relativistic case, i.e. for velocities much smaller than the speed of light.

Measurement

→ Main article: Speed measurement

The easiest way to determine the speed is to measure,

what time is needed for a certain distance or
which distance is covered in a given time interval.

In both cases, only an average speed is actually measured. However, if the distance or time interval is chosen short enough or the motion is approximately uniform, satisfactory accuracies can be achieved with both methods. An example for method 1 would be the measurement of the speed of light according to Hippolyte Fizeau. Method 2 is used, among other things, when velocity values are calculated from GPS data.

The speed of a vehicle can be easily determined with a tachometer. This actually measures the speed of the wheel, which is directly proportional to the speed.

However, virtually any other velocity-dependent effect can also be used for a measurement method, such as the Doppler effect in Doppler radar, momentum in the ballistic pendulum, or dynamic pressure in the Prandtl probe.

Units

The SI unit of speed is meters per second (m/s). Another common unit of speed is kilometers per hour (km/h).

In everyday language, the term "kilometer per hour" is also used. Since in physics such a composition of two units (here: "hour" and "kilometer") is understood as a multiplication of these units, the term "kilometer per hour" is normally not used in the natural sciences.

As a non-metric unit, miles per hour (mph) is used primarily in the USA and some other English-speaking countries. In maritime and aviation, the unit knot (kn) is also commonly used. One knot is one nautical mile (sm) per hour. Vertical speeds in powered aviation are often expressed in feet per minute (LFM).

Almost only in aviation is the Mach number used, which does not specify an absolute quantity, but indicates the ratio of the speed to the local speed of sound. The speed of sound is strongly dependent on temperature but not on air pressure. The reason for using this number is that aerodynamic effects depend on it.

Conversion of common speed units:

	Meter per second	Kilometers per hour	Knots (= nautical miles per hour)	Miles per hour	Speed of light
1 m/s	00 1	00 3,6	00 1,944	00 2,237	0 3,336 · 10−9
1 km/h	00 0,2778	00 1	00 0,5400	00 0,6215	0 9,266 · 10−10
1 kn	00 0,5144	00 1,852	00 1	00 1,151	0 1,716 · 10−9
1 mph	00 0,4469	00 1,609	00 0,8688	00 1	0 1,491· 10−9
1	00 299792458	00 1,079 · ¹⁰⁹	00 5,827 · ¹⁰⁸	00 6,707 · ¹⁰⁸	00 1

Note: The conversion factors in bold are exact, all others rounded to four valid digits.

Velocities and reference frame

Depending on the reference system or coordinate system used, different designations have become common:

In the homogeneous gravity field, a Cartesian coordinate system is often used. Velocities directed parallel to the gravitational acceleration ${\vec {g}}$ usually called vertical velocities, those orthogonal to this direction horizontal velocities.

For polar coordinates, the radial velocity ${\vec {v}}_{\mathrm {r} }$ the component of the velocity vector in the direction of the location vector, i.e. along the line connecting the moving object and the coordinate origin. The component perpendicular to it is called the circumferential velocity ${\vec {v}}_{\perp }$ . Thus, ${\vec {v}}={\vec {v}}_{\perp }+{\vec {v}}_{\mathrm {r} }$ . The vector product of the angular velocity and the location vector gives the circumferential velocity: ${\vec {v}}_{\perp }={\vec {\omega }}\times {\vec {r}}$ .

For movements on a circular path around the coordinate origin, but also only in this case, the radial velocity is zero and the circumferential velocity is equal to the tangential velocity, i.e. the path velocity along the tangent to the path curve.

From the change of the distance to the coordinate origin (radius) follows the radial velocity: ${\vec {v}}_{\mathrm {r} }={\dot {r}}\,{\frac {\vec {r}}{|{\vec {r}}|}}$ .

If one assumes that there is a generally valid reference system, the velocities which are measured in this system are called absolute velocities. Speeds which refer to a point which itself moves in this system are called relative speeds. Example: A streetcar is moving at a speed of 50 km/h. A passenger is moving in the streetcar at a speed of 50 km/h. The streetcar is moving at a speed of 50 km/h. In it a passenger moves with a relative velocity (with respect to the streetcar) of 5 km/h. The absolute velocity of the passenger (from the stationary point) is called absolute velocity. His absolute speed (seen from the stationary observer on the street) is therefore 55 km/h or 45 km/h, depending on whether he moves in the direction of travel or against the direction of travel.

However, the principle of relativity states that there is no physical reason why one should single out a particular reference system and favor it over others. All physical laws, which are valid in an inertial system, are also valid in every other. Which movements one regards as "absolute" is therefore completely arbitrary. That is why the term absolute velocity is avoided at least since the special theory of relativity. Instead, all velocities are relative velocities. From this principle of relativity follows, together with the invariance of the speed of light, that velocities may not - as tacitly assumed in the above example - simply be added. Instead, the relativistic addition theorem applies to velocities. However, this becomes noticeable only at very high velocities.

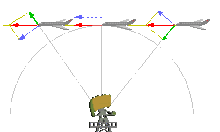
Passing aircraft with velocity (red), radial velocity (green) and tangential velocity (blue).

Velocity of numerous particles

If one considers a system of many particles, it is usually no longer meaningful or even possible to specify a certain velocity for each individual particle. Instead, one works with the velocity distribution, which indicates how often a certain range of velocities occurs in the particle ensemble. For example, in an ideal gas, the Maxwell-Boltzmann distribution applies (see the accompanying figure): most particles have a velocity near the most probable velocity indicated by the maximum of the Maxwell-Boltzmann distribution. Very small and very large velocities also occur, but are assumed by very few particles. The position of the maximum is temperature dependent. The hotter the gas is, the higher is the most probable velocity. More particles then reach high velocities. This shows that the temperature is a measure for the average kinetic energy of the particles. However, very high velocities are not completely excluded even at low temperatures. The velocity distribution can be used to explain many physical transport phenomena, such as diffusion in gases.

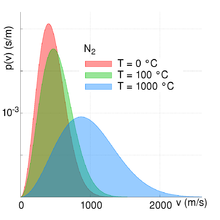
Temperature dependence of the velocity distribution for nitrogen

Flow velocity of a fluid

Shaft velocity

→ Main article: Sound velocity, phase velocity and group velocity

The complex motion of waves makes it necessary to use different speed terms. (In particular, the word propagation velocity can mean different things).

The speed of deflection of mechanical waves is called velocity. The best known example is the speed of vibration of air particles in a sound wave.
The velocity with which a point of certain phase moves forward is called phase velocity. It holds: $v_{\mathrm {p} }={\frac {\lambda }{T}}={\frac {\omega }{k}}$ . Here λ $\lambda$ is the wavelength, is the period, ω $\omega$ angular frequency, and is the angular wavenumber. The speed at which wave crests travel in the ocean is a typical example of a phase velocity.
The velocity at which a whole wave packet travels is called the group velocity: $v_{\mathrm {g} }={\frac {\partial \mathbf {\omega } }{\partial \mathbf {k} }}$ .

Phase and group velocities coincide only in rare cases (e.g. propagation of light in vacuum). As a rule, they differ. An illustrative extreme example is the locomotion of snakes: If we take the snake as a wave, the velocity of its progress is a group velocity. The phase velocity, however, is zero when snaking, because the places where the snake's body curves to the right or left are given by the ground and do not move over the ground.

As a rule, the phase velocity of a physical wave depends on the frequency or the circular wave number. This effect is called dispersion. Among other things, it is responsible for the fact that light of different wavelengths is refracted differently by a prism.

The red point moves with phase velocity and the green points with group velocity

Relativity

→ Main article: Special relativity

From the laws of classical physics follows for velocities among other things:

The measured values for lengths and times are independent of the state of motion (and thus the speed) of the observer. In particular, all observers agree on whether two events occur simultaneously or not.
When the reference system is changed, the Galilean transformation applies. This means that velocities of movements which are superimposed may be added vectorially.
There is no theoretical upper limit for the speed of movements.
Although it is not required by the laws of classical physics, it was generally assumed before Einstein that there was a universal reference frame, the "ether", for all velocities. If this were so, the speed of propagation of electromagnetic waves would have to depend on the state of motion of the receiver.

The latter dependence could not be proved by the Michelson-Morley experiment. Einstein postulated that the principle of relativity, which was already known from classical mechanics, must also be applied to all other phenomena of physics, especially the propagation of light, and that the speed of light is independent of the state of motion of the sender. From this he concluded that the above statements of classical mechanics must be modified. In detail this means:

The measured values for lengths and times depend on the state of motion (and thus the speed) of the observer (see time dilation and length contraction). Also the simultaneity is relative.
When the reference frame is changed, the Lorentz transformation applies. This means that velocities of movements which overlap must not simply be added vectorially.
Movements of bodies can only occur at speeds lower than the speed of light. Information can also not be transmitted faster than the speed of light.
There is no "ether".

However, the effects resulting from special relativity become noticeable only at very high velocities. The Lorentz factor, which is decisive for time dilation and length contraction, results in a deviation of more than one percent only for velocities of $v>4{,}2\cdot 10^{7}\,\mathrm {\tfrac {m}{s}}$ a deviation of more than one percent. Consequently, classical mechanics is an extremely accurate approximation for even the fastest spacecraft built to date.

Questions and Answers

Q: What is velocity?

A: Velocity is a measure of how fast something moves in a particular direction. It requires both magnitude and direction to define it.

Q: What does speed tell us?

A: Speed tells us the rate at which an object moves, but not in which direction.

Q: How can velocity be defined?

A: Depending on the frame of reference, velocity can be defined with many mathematical concepts required for making the correct analysis.

Q: What two components make up velocity?

A: Velocity is made up of speed and direction.

Q: Is speed part of velocity?

A: Yes, speed is one part of velocity; direction is the other part.

Q: Can you give an example of how to calculate velocity?

A: For example, if an object moves east at 9 metres per second (9 m/s), then its velocity would be 9 m/s to the east.