Euclidean vector

The title of this article is ambiguous. For other meanings, see Vector (disambiguation).

In a general sense, in linear algebra, a vector (lat. vector "carrier, driver") is understood to be an element of a vector space, that is, an object that can be added to other vectors and multiplied by numbers called scalars. Vectors in this general sense are discussed in the article Vector Space.

In the narrower sense, in analytic geometry a vector is understood to be a mathematical object that describes a parallel displacement in the plane or in space. A vector can be represented by an arrow that connects an original image point with its image point. Arrows that are of the same length, parallel and oriented in the same way describe the same vector. In Cartesian coordinates, vectors are represented by pairs of numbers (in the plane) or triples (in space), often written one below the other (as "column vectors"). Vectors can be added and multiplied by real numbers (scalars).

Motivated by the coordinate representation of geometric vectors, -tuples of real numbers, i.e. elements of $\mathbb {R} ^{n}$ , are called vectors or coordinate vectors. This is justified by the fact that every -dimensional real vector space is isomorphic to the vector space $\mathbb {R} ^{n}$ . Examples of such use of the vector notion can be found namely in economic mathematics.

This article deals mainly with vectors in the geometric sense and with vectors as elements of the "tuple space" $\mathbb {R} ^{n}$ .

Closely related to geometric vectors are vector quantities in physics. These are physical quantities that have a magnitude and a direction, and are often represented by arrows whose length corresponds to the magnitude of the quantity. Examples are velocity, acceleration, momentum, force, electric and magnetic field strength.

History

Vector calculus was founded by Hermann Günter Graßmann, who published his Ruler Ausdehnungslehre in 1844, a book of over three hundred pages. Among others, René Descartes and August Ferdinand Möbius, a student of Carl Friedrich Gauss, are considered as precursors. Around 1850, the Irish mathematician Matthew O'Brien used the vector calculus to describe mechanical facts, but remained largely ignored. Almost simultaneously, William Rowan Hamilton developed his similar theory of quaternions, which he published in the book Lectures on Quaternions in 1853 and in the work Elements of Quaternions in 1866. In Germany the vector calculus was spread especially by lectures and books of Alfred Bucherer, August Föppl, Carl Runge, Fischer, v. Ignatowsky and Richard Gans.

Spelling and speech

Variables representing vectors are often marked with an arrow ( $\vec a, \vec{v}$ )school mathematics and physics.) Especially in English-speaking countries, they are also written in bold ( $\mathbf {v}$ , $\boldsymbol v$ or v). In manuscripts, this is often represented by underlining ( $\underline v$ ) or similar. In the past, writing with small Fraktur letters ( $\mathfrak{a}, \mathfrak{b}, \mathfrak{v}$ ) was also common in some cases, handwritten in German cursive or Sütterlin script. Frequently chosen letters are $\vec a, \vec b, \vec c$ and $\vec u, \vec v, \vec w$ . The corresponding Latin letter without vector label usually stands for the length (magnitude) of the vector: $v = |\vec{v}|$

Geometry

Definition

In geometry, a vector is an object that describes a parallel displacement in the plane or in space. A displacement can be represented by an arrow connecting an original image point with its image point. Arrows that are parallel, of the same length and direction describe the same displacement and thus represent the same vector. For example, in the image on the right, the arrow from to , the arrow from to and the arrow from to same shift of 7 units to the right and 3 units up. They all represent the same vector ${\vec {v}}={\overrightarrow {AA'}}={\overrightarrow {BB'}}={\overrightarrow {CC'}}$ . Formally, therefore, vectors can be defined as follows:

An arrow is a directed line, that is, a line in which a sequence of endpoints is specified. Two arrows are called equivalent if they are parallel, of the same length and directed in the same way. This defines an equivalence relation on the set of arrows of the plane or space. The equivalence classes are called vectors.

Another way is to identify a vector with the parallel displacement represented by it. "Vector" is then just another way of saying "parallel displacement".

The vector describing a displacement mapping point to point ${\overrightarrow {AB}}$ written as and represented graphically by an arrow pointing from point to point We say, "The vector $\vec{a}=\overrightarrow{AB}$ maps to ," or, "The vector $\vec{a}=\overrightarrow{AB}$ connects and ." In this case, the point called the shaft, starting or starting point and the tip or end point of the vector arrow. The distance between the two points is called the length or magnitude of the vector.

The reverse vector $\overrightarrow{BA}$ that connects to is called the opposite vector to ${\overrightarrow {AB}}$ . The vector $\overrightarrow{AA}$ , which maps a point is called a null vector and is $\vec o$ denoted by $\vec 0$ or the only vector that cannot be represented graphically by an arrow.

Location and direction vectors

→ Main article: Location vector

Vectors can also be used to denote points in space. Thus, the location of the point can be denoted by the vector

$\vec{p}=\overrightarrow{OP}$

can be represented. This vector is called the location vector belonging to the point Thereby denotes the coordinate origin, which is the starting point for all location vectors.

To distinguish them from each other, vectors as described in the previous section are also called direction vectors. Two direction vectors are identical if they have the same magnitude and direction. However, as shown, they can have any point in space as a starting point, while location vectors always start from the coordinate origin.

This distinction is important, among other things, in analytic geometry. There, for example, a straight line is described by the following equation:

$\vec{x}=\vec{p}+r\cdot\vec{v}$

The support vector ${\vec {p}}$ is the location vector of an arbitrarily chosen "support point" of the straight line. The direction vector ${\vec {v}}$ gives the direction of the straight line. Because stands for any real number, is ${\vec {x}}$ the location vector of any point of the straight line.

Representation in coordinates

If, as in the figure above, a rectilinear coordinate system is given, a vector of the plane can be described by an ordered pair of numbers, a vector in space by a triplet of numbers. Usually, these coordinates are written one below the other as so-called column vectors. For the vector in the plane describing the displacement by 7 units to the right (in direction) and 3 units upward (in direction), write $\vec v = \tbinom 7 3$ . The vector $\tbinom 2 {-5}$ describes a displacement of 2 units in the direction and -5 units in the direction, that is, 2 units to the right and 5 units down. Correspondingly, in space the vector describes $\left(\begin{smallmatrix} 3\\-2\\4 \end{smallmatrix}\right)$ a displacement by 3 units in direction, 2 units in negative direction and 4 units in -direction.

The coordinates of a vector can be calculated as the difference of the coordinates of the end and start point. In the example above, and have coordinates A(-6|-1) and A'(1|2) . The coordinates of the connection vector $\vec v = \overrightarrow{AA'}$ then calculated as follows:

$\vec v = \overrightarrow{AA'} = \begin{pmatrix} 1 - (-6) \\ 2 - (-1) \end{pmatrix} = \begin{pmatrix} 7 \\ 3 \end{pmatrix}$

Amount and direction

Unlike scalars, vectors have a direction. A vector is therefore characterized by its magnitude and its direction. The direction is given on the one hand by the axis position, on the other hand by the direction sense. The sense of direction indicates in which of the two directions along the axis the vector points. A change of sign in the magnitude of the vector corresponds to the reversal of the sense of direction.

A vector from start point A to end point B and its length

Displacement of triangle ABC by shifting the points by $\vec {v }$

Arithmetic operations

Addition and subtraction

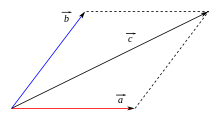
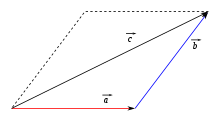
The addition of two geometric vectors corresponds to the back-to-back execution of the associated displacements. If the vector ${\vec {a}}$ represents the displacement mapping the point to and the displacement associated to ${\vec {b}}$ maps the point to then $\vec a + \vec b$ describes the displacement mapping to

${\overrightarrow {PQ}}+{\overrightarrow {QR}}={\overrightarrow {PR}}$

Geometrically, therefore, two vectors ${\vec {a}}$ and be ${\vec {b}}$ added by representing the two vectors by arrows in such a way that the start point of the second arrow coincides with the end point of the first arrow. The sum ${\vec {c}}={\vec {a}}+{\vec {b}}$ is then represented by the arrow from the start point of the first to the end point of the second arrow.

Alternatively, the two vectors are represented by arrows with a common starting point and this figure is completed to a parallelogram. The diagonal arrow from the common starting point to the opposite corner then represents the sum of the two vectors. In physics, this construction is used for the parallelogram of forces.

In coordinates one calculates the sum component-wise: For the sum of the two vectors

$\vec a = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}$ and $\vec b = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}$

applies

$\vec{a}+\vec{b} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix}a_1+b_1 \\ a_2+b_2 \\ a_3+b_3\end{pmatrix}$ .

The associative and commutative laws apply to the addition of vectors.

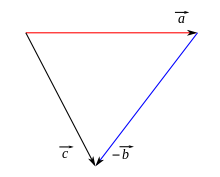
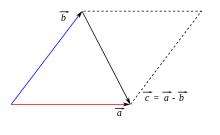
For the difference of two vectors ${\vec {a}}$ and ${\vec {b}}$ holds true

$\vec{a}-\vec{b} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} - \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix}a_1-b_1 \\ a_2-b_2 \\ a_3-b_3\end{pmatrix}$ .

It can be interpreted geometrically in two ways:

As the sum of ${\vec {a}}$ with the counter vector $-{\vec {b}}$ of ${\vec {b}}$ . One places the starting point of an arrow representing the counter vector of ${\vec {b}}$ the end point of the arrow ${\vec {a}}$ representing
As that vector which, when ${\vec {b}}$ added to ${\vec {a}}$ gives even If ${\vec {a}}$ and ${\vec {b}}$ by arrows with the same starting point, is $\vec a - \vec b$ represented by the arrow leading from the endpoint of the second vector to the endpoint of the first vector.

If two vectors are added (subtracted), their amounts add (subtract) only if the vectors are collinear and have the same orientation. In the general case, however, the triangle inequality applies:

$\left|{\vec {a}}+{\vec {b}}\right|\leq \left|{\vec {a}}\right|+\left|{\vec {b}}\right|$

Multiplication with a scalar

Vectors can be multiplied by real numbers (often called scalars to distinguish them from vectors) (scalar multiplication, also called S-multiplication):

$r\vec{a} = r \, \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} = \begin{pmatrix}ra_1 \\ ra_2 \\ ra_3\end{pmatrix}$

The length of the resulting vector is $|r|\cdot|\vec{a}|$ . If the scalar is positive, the resulting vector points in the same direction as the original one, if it is negative, in the opposite direction.

For vector addition and multiplication by a scalar, the distributive law applies:

$r\cdot(\vec a + \vec b) = r\vec a + r\vec b$

The same applies to the addition of two scalars:

$(r+s)\cdot\vec a = r\vec a + s\vec a$

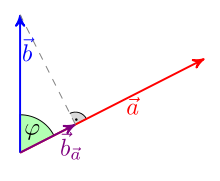
Scalar product

→ Main article: Scalar product

The scalar product (or inner product) of two vectors ${\vec {a}}$ and $\vec b,$ so called because the result is a scalar, is written as ${\vec {a}}\cdot {\vec {b}},\ {\vec {a}}\circ {\vec {b}},\ {\vec {a}}\bullet {\vec {b}}$ or ⟨ $\langle {\vec a,\vec b} \rangle$ is noted and is.

${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\,\cos \varphi ,$

where φ is $\varphi$ the angle enclosed between the two vectors (see also cosine). If the two vectors are perpendicular to each other, then ${\vec {a}}\cdot {\vec {b}}=0$ , since $\cos \varphi = \cos 90^\circ = 0$ holds.

In the Cartesian coordinate system, the scalar product is calculated to be

$\vec{a}\cdot\vec{b} = \begin{pmatrix}a_1 \\ a_2 \\ a_3 \end{pmatrix}\cdot\begin{pmatrix}b_1 \\ b_2 \\ b_3 \end{pmatrix} = a_1b_1+a_2b_2+a_3b_3,$

in particular, the square of a vector is

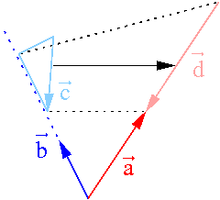
$\vec{a}\cdot\vec{a} = \begin{pmatrix}a_1 \\ a_2 \\ a_3 \end{pmatrix}\cdot\begin{pmatrix}a_1 \\ a_2 \\ a_3 \end{pmatrix} = a_1^2+a_2^2+a_3^2.$

Geometrically, the scalar product can also be understood as follows (see figure): One projects one vector ${\vec {b}}$ perpendicular to the other ${\vec {a}}$ and thus obtains the vector $\vec b_{\vec a}$ . If the angle φ {\displaystyleenclosed by the two vectors is $\varphi$ an acute angle, } $\vec b_{\vec a}$ points in the same direction as ${\vec {a}}$ . In this case, the scalar product is obtained by multiplying the two magnitudes of ${\vec {a}}$ and $\vec b_{\vec a}$ . This number is positive. On the other hand, if the angle is an obtuse angle, the projection is antiparallel to ${\vec {a}}$ and therefore the scalar product has a negative sign. If the two vectors enclose a right angle ( $\varphi = 90^\circ$ ), then the length of the projected vector is zero and so is the scalar product. (Swapping the two vectors in this procedure yields the same value).

This operation is often used in physics, for example, to calculate work when the direction of the force does not coincide with the direction of motion.

For the scalar product the commutative law applies

$\vec a \cdot \vec b = \vec b \cdot \vec a$

and the distributive law

${\vec {a}}\cdot ({\vec {b}}+{\vec {c}})={\vec {a}}\cdot {\vec {b}}+{\vec {a}}\cdot {\vec {c}}.$

Cross product

→ Main article: Cross product

The cross product (also vector product, outer product, or vector product) $\vec a\times\vec b$ (pronounced as "a cross b") of two vectors in three-dimensional Euclidean vector space is a given vector perpendicular to the ${\vec {b}}$ plane spanned by ${\vec {a}}$ and The length $|\vec a\times\vec b|$ this vector is equal to the area of the parallelogram with sides ${\vec {a}}$ and ${\vec {b}}$ , so

$|{\vec {a}}\times {\vec {b}}|=|{\vec {a}}|\cdot |{\vec {b}}|\cdot |{\sin \theta }|,$

where the angle enclosed by the two vectors $\theta$ is denoted here by θ The cross product of two collinear vectors therefore gives the zero vector.

In the three-dimensional Cartesian coordinate system, the cross product can be calculated as follows:

$\vec{a}\times\vec{b} = \begin{pmatrix}a_1 \\ a_2 \\ a_3 \end{pmatrix}\times\begin{pmatrix}b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix}a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{pmatrix}$

The cross product is anticommutative, i.e., it holds

$\vec{a}\times\vec{b} = -(\vec{b}\times\vec{a}).$

Spat product

→ Main article: Spat product

The combination of cross and scalar product in the form

$({\vec {a}},{\vec {b}},{\vec {c}})=({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}$

is called a spar product. The result is a scalar. Its magnitude is the volume of the spar spanned by the three vectors. If the three vectors form a right system, then is $({\vec a},{\vec b},{\vec c})$ positive. If they form a link system, then is $({\vec a},{\vec b},{\vec c})$ negative. If the vectors are linearly dependent, then $({\vec {a}},{\vec {b}},{\vec {c}})=0$ .

Length/amount of a vector

In Cartesian coordinates, the length of vectors can be calculated according to the Pythagorean theorem:

$a=|{\vec {a}}|={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}}}$

This corresponds to the so-called Euclidean norm. The length can also be given in an alternative notation as the root of the scalar product:

$a=|{\vec {a}}|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}$

Vectors of length 1 are called unit vectors. If a vector has the length 0, it is the zero vector.

For vector quantities in physics, one speaks of the magnitude of a vector instead of the length. One can consider a vectorial physical quantity ${\vec {v}}$ as a pair $(\vec{e}_v, |\vec{v}|)$ of direction of the quantity as unit vector $\vec{e}_v$ and magnitude of the quantity along this direction. The unit of the magnitude is equal to the unit of the physical quantity. For example, the velocity

${\vec {v}}={\begin{pmatrix}3\\-4\\0\end{pmatrix}}\,\mathrm {\frac {m}{s}}$

of a helicopter flying at a constant altitude in a southeasterly direction through

${\vec {e}}_{v}={\frac {1}{|{\vec {v}}|}}{\vec {v}}={\begin{pmatrix}{\tfrac {3}{5}}\\-{\tfrac {4}{5}}\\0\end{pmatrix}}$

and

$|{\vec {v}}|={\sqrt {3^{2}+(-4)^{2}+0^{2}}}\,\mathrm {\frac {m}{s}} =5\,\mathrm {\frac {m}{s}}$

represent. The magnitude of the path velocity v(t) during horizontal throw (starting velocity in -direction $v_{x}$ , current velocity in -direction $v_{y}(t)$ ) can be expressed as

$v(t)={|{\vec {v(t)}}|}={\sqrt {v_{\mathrm {x} }^{2}+v_{\mathrm {y} }^{2}}}.$

Dyadic product

→ Main article: Dyadic product

The dyadic or tensorial product ${\vec {a}}\otimes {\vec {b}}$ or ${\vec {a}}{\vec {b}}$ (spoken as "a dyadic b") of two vectors forms a dyad. Dyads allow one vector to be mapped linearly onto another vector, see figure. The portion of a vector $\vec c$ in the direction of vector ${\vec {b}}$ is thereby ${\vec {a}}$ brought into the direction of vector and thereby stretched or compressed. The mapping is done with the above scalar product:

$({\vec {a}}\otimes {\vec {b}})\cdot {\vec {c}}:=({\vec {b}}\cdot {\vec {c}}){\vec {a}}$

In the three-dimensional Cartesian coordinate system, the dyadic product can be calculated as follows:

${\vec {a}}\otimes {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\otimes {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}b_{1}&a_{1}b_{2}&a_{1}b_{3}\\a_{2}b_{1}&a_{2}b_{2}&a_{2}b_{3}\\a_{3}b_{1}&a_{3}b_{2}&a_{3}b_{3}\end{pmatrix}}$

The dyadic product is not commutative, i.e., in general

${\vec {a}}\otimes {\vec {b}}\neq {\vec {b}}\otimes {\vec {a}},$

but distributive with vector addition:

${\begin{aligned}({\vec {a}}+{\vec {b}})\otimes {\vec {c}}={\vec {a}}\otimes {\vec {c}}+{\vec {b}}\otimes {\vec {c}}\\{\vec {a}}\otimes ({\vec {b}}+{\vec {c}})={\vec {a}}\otimes {\vec {b}}+{\vec {a}}\otimes {\vec {c}}\end{aligned}}$

It is also compatible with scalar multiplication:

$\lambda ({\vec {a}}\otimes {\vec {b}})=(\lambda {\vec {a}})\otimes {\vec {b}}={\vec {a}}\otimes (\lambda {\vec {b}})=\lambda {\vec {a}}\otimes {\vec {b}}$

The dyadic product gives rise to a new class of linear algebra objects, the matrices and linear mappings, depending on whether we are computing in coordinate space or vector space. By linking several dyads (as in ${\vec {a}}\otimes {\vec {b}}\otimes {\vec {c}}\dotsm$ ) give rise to higher level dyads. Dyads form a special case of tensors. Tensors play an important role in continuum mechanics, Maxwell's equations of electromagnetism, and general relativity. An overview of the tensor algebra is given in the collection of formulas Tensoralgebra.

Vector addition ${\vec {c}}={\vec {a}}+{\vec {b}}\,$ by parallelogram construction.

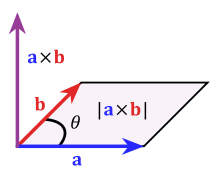
Illustration of the cross product

Mapping a vector $\vec c$ to vector ${\vec {d}}=({\vec {a}}\otimes {\vec {b}})\cdot {\vec {c}}$

Vector subtraction ${\vec {c}}={\vec {a}}+(-{\vec {b}})={\vec {a}}-{\vec {b}}$ by arrow string with countervector

Vector subtraction ${\vec {c}}={\vec {a}}-{\vec {b}}$ by construction with arrows with the same starting point

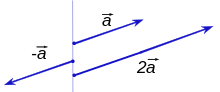
Scalar multiplication

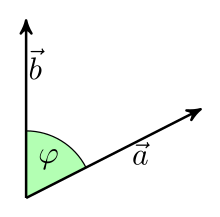
The scalar product of two vectors depends on the length of the vectors and the included angle

Orthogonal projection $\vec b_{\vec a}$ vector ${\vec {b}}$ onto the ${\vec {a}}$ direction determined by

Vector addition ${\vec {c}}={\vec {a}}+{\vec {b}}\,$ by arrow stringing.

Component notation

As an alternative to the notation presented here as column vectors, vectors can also be represented in component notation. Here $a_{i}$ usually stands for the individual components of the vector ${\vec {a}}$ with respect to the standard basis. Thus, the arithmetic operations with respect to the standard basis can be written as follows:

	Column vectors	Component notation
Addition/Subtraction	${\vec {c}}={\vec {a}}\pm {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\pm {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}\pm b_{1}\\a_{2}\pm b_{2}\\a_{3}\pm b_{3}\end{pmatrix}}$	$c_{i}=a_{i}\pm b_{i}$
Scalar product	$c={\vec {a}}\cdot {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\cdot {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$	$c=\sum _{i}a_{i}b_{i}$ respectively: $c=a_{i}b_{i}$
Amount	$a=\|{\vec {a}}\|={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}}}$	$a={\sqrt {\sum _{i}a_{i}^{2}}}$ respectively: $a={\sqrt {a_{i}a_{i}}}$
Cross product	${\vec {c}}={\vec {a}}\times {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\times {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{pmatrix}}$	$c_{i}=\sum _{jk}\varepsilon _{ijk}a_{j}b_{k}$ respectively: $c_{i}=\varepsilon _{ijk}a_{j}b_{k}$

↑ ^{a b c} Using Einstein's summation convention.
↑ ε $\varepsilon_{ijk}$ is the Levi-Civita symbol and is +1 for even permutations of (1, 2, 3), -1 for odd permutations, and 0 otherwise.

See also the section Coordinates and components of a vector below.

n-tuples and column vectors

In generalization of the coordinate representation of geometric vectors, elements of $\mathbb {R} ^{n}$ , i.e., -tuples of real numbers, are called vectors if the arithmetic operations typical for vectors, addition and scalar multiplication, are performed with them. As a rule, the are written as so-called column vectors, i.e. their entries are one below the other.

Addition and scalar multiplication

The addition of two vectors $\vec x, \vec y \in \R^n$ and the scalar multiplication of a vector by a number $r\in \mathbb {R}$ are defined component-wise:

${\vec {x}}+{\vec {y}}={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}+{\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}={\begin{pmatrix}x_{1}+y_{1}\\\vdots \\x_{n}+y_{n}\end{pmatrix}},\quad r{\vec {x}}=r{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}={\begin{pmatrix}rx_{1}\\\vdots \\rx_{n}\end{pmatrix}}$

The set $\mathbb {R} ^{n}$ with these links forms a vector space over the body $\mathbb {R}$ . This so-called coordinate space is the standard example of an -dimensional $\mathbb {R}$ -vector space.

Standard scalar product

→ Main article: Standard scalar product

The standard scalar product is defined by

$\vec x \cdot \vec y = \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \cdot \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix} = x_1 y_1 + \dotsb + x_n y_n$ .

With this scalar product, the $\mathbb {R} ^{n}$ is a Euclidean vector space.

Multiplication with a matrix

→ Main article: Matrix vector product

If $A\in \mathbb {R} ^{m\times n}$ is a ( $m\times n$ )-matrix and $\vec x \in \R^n$ a column vector, then can be ${\vec {x}}$ written as a one-column matrix in $\R^{n \times 1}$ and $A \, \vec x$ form the matrix vector product The result is a column vector in $\mathbb {R} ^{m}$ :

$A\,{\vec {x}}={\begin{pmatrix}a_{11}&\dots &a_{1n}\\\vdots &\ddots &\vdots \\a_{m1}&\dots &a_{mn}\end{pmatrix}}\,{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}={\begin{pmatrix}a_{11}x_{1}+\dotsb +a_{1n}x_{n}\\\vdots \\a_{m1}x_{1}+\dotsb +a_{mn}x_{n}\end{pmatrix}}$

Multiplication by a ( $m\times n$ )-matrix is a linear mapping from $\mathbb {R} ^{n}$ to $\mathbb {R} ^{m}$ . Any linear mapping can be represented as a multiplication by a matrix.

Length or standard

→ Main article: Euclidean norm

The length or norm of a vector is given by the square root of the scalar product with itself:

$|\vec x| = \sqrt{\vec x \cdot \vec x} = \sqrt{x_1^2 + \dotsb + x_n^2}$

Besides this Euclidean norm, other norms are also used, see p-norm.

Row and column vectors

If we consider vectors as matrices, an $n \times 1$ matrix is a column vector

${\vec {x}}={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}},$

for which there is a $1 \times n$ matrix

${\vec {x}}^{\top }=(x_{1}\ \dotsc \ x_{n})$

as the associated row vector, where is ${\vec {x}}^{\top }$ the transpose of ${\vec {x}}$ In this notation, the standard scalar product is nothing but the matrix product of a $1 \times n$ with an $n \times 1$ matrix:

${\vec {x}}\cdot {\vec {y}}={\vec {x}}^{\top }{\vec {y}}=(x_{1}\ \dotsc \ x_{n})\ {\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}=x_{1}y_{1}+\dotsb +x_{n}y_{n}$

The dyadic product represents itself as the matrix product of an $n \times 1$ with a $1 \times n$ , and then yields an $n\times n$ matrix:

${\vec {x}}\otimes {\vec {y}}={\vec {x}}\,{\vec {y}}^{\top }={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}\ (y_{1}\ \dotsc \ y_{n})={\begin{pmatrix}x_{1}y_{1}&\ldots &x_{1}y_{n}\\\vdots &\ddots &\vdots \\x_{n}y_{1}&\ldots &x_{n}y_{n}\end{pmatrix}}$

Vector properties

Linear dependence

Vectors ${\vec {a}}_{1},{\vec {a}}_{2},\dotsc ,{\vec {a}}_{m}$ ( $m\ge 1$ ) are called linearly dependent if there is a solution for the following equation where not r_i=0 hold for all coefficients:

$r_{1}\cdot {\vec {a}}_{1}+r_{2}\cdot {\vec {a}}_{2}+\dotsb +r_{m}\cdot {\vec {a}}_{m}={\vec {0}}{\text{ mit }}r_{i}\in \mathbb {R}$

However, if no coefficients $r_{i}$ found that satisfy this condition, then the vectors are called linearly independent.

In the case m=1 holds: The zero vector is linearly dependent, every other vector is linearly independent.

For in the case of linear dependence, at least one of the vectors m>1 represented as a linear combination of the others.

To define a coordinate system for an -dimensional space, one needs exactly linearly independent basis vectors. Then one can write each vector of this space uniquely as a linear combination of the basis vectors. More than vectors in the -dimensional space are always linearly dependent.

Collinearity of two vectors

Two linearly dependent vectors ${\vec {a}}$ and ${\vec {b}}$ also called collinear. In three-dimensional space it holds

$\vec{a} \times \vec{b} = \vec{0}.$

Every vector is collinear with the zero vector. But if there are two vectors different from the zero vector, they are collinear exactly if

$\vec{a} = r \cdot \vec{b}$

for an $r\in \mathbb {R} \setminus \{0\}$ is satisfied. They are parallel if positive and antiparallel if is negative.

Orthogonality

Two vectors ${\vec {a}}$ and $\vec{b}$ are orthogonal if their scalar product is equal to 0:

$\vec{a} \cdot \vec{b} = 0$

For geometric vectors with positive length this means that they enclose a right angle, see scalar product. The zero vector is orthogonal to any vector.

Standardization

A vector ${\hat {a}}$ (read "a roof") is called a unit vector or normalized if it has length 1. One normalizes a vector $\vec{a}\neq \vec{0}$ , by dividing it by its length, i.e., multiplying it by the reciprocal of its length:

$\hat a = \frac{\vec{a}} {|\vec{a}|}$

The vector ${\hat {a}}$ has the same direction as ${\vec {a}}$ , but length 1. Other notations for ${\hat {a}}$ are $\vec e_a$ , $\vec a_0$ or $\vec a{}^\circ$ .

Unit vectors are important in the representation of coordinate systems.

Coordinates and components of a vector

→ Main article: Vector space basis

For example, the most widely used coordinate system, the Cartesian, is an orthonormal system because it is derived from the three mutually orthogonal unit vectors $\hat e_1$ , $\hat e_2$ and $\hat e_3$ of the standard basis. The coordinates of a vector are then the scalar products of the vector with the basis vectors:

$a_i = \vec a \cdot \hat e_i$

Thus, any vector can be represented as a linear combination of the basis vectors by writing it as the sum of its components with respect to the basis:

${\vec {a}}=\sum _{i=1}^{3}\left({\vec {a}}\cdot {\hat {e}}_{i}\right){\hat {e}}_{i}=\left({\vec {a}}\cdot {\hat {e}}_{1}\right){\hat {e}}_{1}+\left({\vec {a}}\cdot {\hat {e}}_{2}\right){\hat {e}}_{2}+\left({\vec {a}}\cdot {\hat {e}}_{3}\right){\hat {e}}_{3}$

By changing to another orthonormal basis ${\hat {g}}_{1,2,3}$ the vector gets other coordinates $a_{i}^{\prime }={\vec {a}}\cdot {\hat {g}}_{i}$ and other components:

${\vec {a}}=\sum _{i=1}^{3}\left({\vec {a}}\cdot {\hat {g}}_{i}\right){\hat {g}}_{i}=\left({\vec {a}}\cdot {\hat {g}}_{1}\right){\hat {g}}_{1}+\left({\vec {a}}\cdot {\hat {g}}_{2}\right){\hat {g}}_{2}+\left({\vec {a}}\cdot {\hat {g}}_{3}\right){\hat {g}}_{3}$

More generally, any three but linearly independent vectors can be used as a vector space basis.

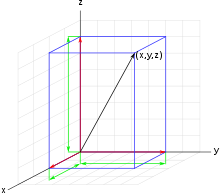
Vector (black) with components (red) and coordinates (green) with respect to a coordinate system (gray)

Generalizations

The definition of a vector in linear algebra as an element of a vector space is a much broader one, including a wide variety of mathematical objects (numbers, sequences, functions, and transformations) in addition to conventional, geometric vectors.

On the other hand, vectors are just one-step tensors, i.e. tensors with only one index.

Questions and Answers

Q: What is a vector?

A: A vector is a mathematical object that has a size, called the magnitude, and a direction. It is often represented by boldface letters or as a line segment from one point to another.

Q: How do we usually draw vectors?

A: We usually draw vectors as arrows. The length of the arrow is proportional to the vector's magnitude and the direction in which the arrow points to is the vector's direction.

Q: What does it mean when someone asks for directions?

A: When asking for directions, if one says "Walk one kilometer towards the North", that would be a vector, but if they say "Walk one kilometer", without showing a direction, then that would be a scalar.

Q: What are some examples of how vectors can be used?

A: Vectors can be used to show the distance and direction something moved in. They can also be used when asking for directions or navigating an area.

Q: How are vectors represented mathematically?

A: Vectors are often represented by boldface letters (such as u, v, w) or as a line segment from one point to another (as in A→B).

Q: What does it mean when something is referred to as scalar?

A: When something is referred to as scalar it means that there isn't any directional information associated with it; only numerical values such as distance or speed.