Vector space

A vector space or linear space is an algebraic structure used in many subfields of mathematics. Vector spaces form the central object of study in linear algebra. The elements of a vector space are called vectors. They can be added or multiplied by scalars (numbers), the result is again a vector of the same vector space. The term was developed by abstracting these properties from vectors of Euclidean space, so that they can then be transferred to more abstract objects such as functions or matrices.

The scalars with which one can multiply a vector originate from a body. Therefore, a vector space is always a vector space over a certain body. Very often, this is the body $\mathbb {R}$ of the real numbers or the body $\mathbb {C}$ of the complex numbers. We then speak of a real vector space and a complex vector space, respectively.

A basis of a vector space is a set of vectors that allows each vector to be represented by unique coordinates. The number of basis vectors in a basis is called the dimension of the vector space. It is independent of the choice of basis and may be infinite. The structural properties of a vector space are uniquely determined by the body over which it is defined and its dimension.

A basis makes it possible to perform calculations with vectors using their coordinates instead of the vectors themselves, which makes some applications easier.

Vector addition and multiplication with scalars: A vector v (blue) is added to another vector w (red, below). Above, w is stretched by a factor of 2, the result is the sum v + 2-w.

First properties

For all α $\alpha \in K$ and the following statements hold $v,w\in V$

$(-\alpha) \cdot v = - (\alpha \cdot v) = \alpha \cdot (-v)$ .
$\alpha \cdot v = 0_V \quad\Leftrightarrow\quad \alpha =0_K \text{ oder } v =0_V$ .
The equation is $v,w\in V$ uniquely solvable for all ; the solution is .

Examples

Euclidean plane

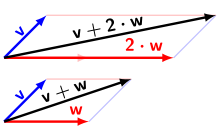
An illustrative vector space is the two-dimensional Euclidean plane $\mathbb R^2$ (in rectangular Cartesian coordinate systems) with the arrow classes (displacements or translations) as vectors and the real numbers as scalars.

$\vec v = ( 2 , 3 )$ is the shift of 2 units to the right and 3 units up,

$\vec w = ( 3 ,-5 )$ the shift by 3 units to the right and 5 units down.

The sum of two shifts is again a shift, and it is the shift obtained by performing the two shifts one after the other:

$\vec v + \vec w = ( 5 ,-2 )$ , i.e., shifting 5 units to the right and 2 units down.

The zero vector $\vec 0 = ( 0 , 0 )$ corresponds to the shift that leaves all points in place, i.e., the identical mapping.

Stretching the displacement ${\vec {v}}$ with a scalar a = 3 from the set of real numbers, we obtain three times the displacement:

$a \cdot \vec v = 3 \cdot ( 2 , 3 ) = ( 6 , 9 )$ .

Everything said about this example is also valid in the real affine plane.

Coordinate space

→ Main article: Coordinate space

If is a body and is a natural number, then the -fold Cartesian product forms

$K^{n}=\{(v_{1},\dots ,v_{n})\mid v_{1},\dots ,v_{n}\in K\},$

the set of all -tuples with entries in , a vector space over . Addition and scalar multiplication are defined component-wise; for $u=(u_{1},u_{2},\dots ,u_{n}),v=(v_{1},v_{2},\dots ,v_{n})\in K^{n}$ , α $\alpha \in K$ one sets:

$u + v = (u_1, u_2, \dots, u_n) + (v_1, v_2, \dots, v_n) = (u_1 + v_1, u_2 + v_2, \dots, u_n + v_n)$

and

$\alpha \cdot v=\alpha \cdot (v_{1},v_{2},\dots ,v_{n})=(\alpha \,v_{1},\alpha \,v_{2},\dots ,\alpha \,v_{n}).$

Often the -tuples are also notated as column vectors, that is, their entries are written one below the other. The vector spaces $K^{n}$ form, in a sense, the standard examples of finite-dimensional vector spaces. Every -dimensional -vector space is isomorphic to the vector space $K^{n}$ . Using a basis, each element of a vector space can be uniquely represented by an element of the $K^{n}$ coordinate tuple.

Function spaces

Principles and definition

→ Main article: Function space

If is a body, is a -vector space, and is an arbitrary set, then on the set F(A,V) of all functions $f \colon A \to V$ , addition and scalar multiplication can be defined pointwise: For $f, g \in F(A,V)$ and α $\alpha \in K$ , the functions $f + g \in F(A,V)$ and α are $\alpha \cdot f \in F(A,V)$ defined by.

(f + g) (x) = f(x) + g(x) for all $x\in A$ and

$(\alpha \cdot f) (x) = \alpha \cdot f(x)$ for all $x\in A$ .

With this addition and scalar multiplication, is F(A,V) a -vector space. In particular, this holds for F(A,K) , so if the target space is chosen to be the body itself. Further examples of vector spaces are obtained as subvector spaces of these function spaces.

In many applications, $K = \R$ , the body of real numbers, or $K=\mathbb {C}$ , the body of complex numbers, and is a subset of $\mathbb {R}$ , $\mathbb {R} ^{n}$ , $\mathbb {C}$ or $\mathbb {C} ^{n}$ . Examples include the vector space of all functions from $\mathbb {R}$ to $\mathbb {R}$ and the subspaces $C^0(\R,\R)$ of all continuous functions and $C^k(\R,\R)$ of all -times continuously differentiable functions from $\mathbb {R}$ to $\mathbb {R}$ .

Space of linear functions

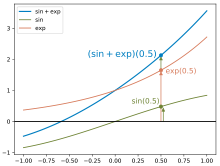
A simple example of a function space is the two-dimensional space of real linear functions, that is, functions of the form

$f\colon\R\to\R,\;x\mapsto a x + b$

with real numbers and . These are those functions whose graph is a straight line. The set of these functions is a subvector space of the space of all real functions, because the sum of two linear functions is again linear, and a multiple of a linear function is also a linear function.

For example, the sum of the two linear functions and with

f(x) = 2x + 3 , g(x) = 3x - 5 ,

the function f + g with

(f + g)(x) = f(x) + g(x) = 2x + 3 + 3x - 5 = (2+3)x + (3-5) = 5x - 2 .

The 3-fold of the linear function is the linear function with

$(3f)(x) = 3 \cdot f(x) = 3 \cdot (2x + 3) = (3 \cdot 2)x + (3 \cdot 3) = 6x + 9$ .

Polynomial Spaces

The set K[X] of polynomials with coefficients from a body forms, with the usual addition and the usual multiplication by a body element, an infinite-dimensional vector space. The set of monomials $\{1,\ x,\ x^2,\ x^3,\ x^4, \dots \}$ is a basis of this vector space. The set of polynomials whose degree is bounded by an $n\in \mathbb {N}$ is upper bounded, forms a subvector space of dimension n+1 . For example, the set of all polynomials of degree less than or equal to 4, that is, all polynomials of the form

ax^4 + b x^3 + c x^2 + d x + e ,

a 5-dimensional vector space with basis $\{1,\ x,\ x^2,\ x^3,\ x^4\}$ .

For infinite bodies one can identify the (abstract) polynomials with the associated polynomial functions. In this approach, the polynomial spaces correspond to subspaces of the space of all functions from to . For example, the space of all real polynomials of degree ≤ $\le 1$ corresponds to the space of linear functions.

Body enlargements

If is a superbody of then with its addition and the restricted multiplication $K\times L\rightarrow L$ as scalar multiplication is a -vector space. The rules to be proved for this follow directly from the body axioms for . This observation plays an important role in the theory of bodies.

For example, $\mathbb {C}$ in this way is a two-dimensional $\mathbb {R}$ -vector space; a basis is $\{1, \mathrm i\}$ . Similarly, $\mathbb {R}$ is an infinite-dimensional $\mathbb {Q}$ -vector space, but where a basis cannot be concretely specified.

Example of addition in functions: The sum of the sine function and the exponential function is $\sin +\exp :\mathbb {R} \to \mathbb {R}$ with $(\sin +\exp )(x)=\sin(x)+\exp(x)$