Transpose

In mathematics, a matrix (plural matrices) is a rectangular arrangement (table) of elements (usually mathematical objects, such as numbers). These objects can then be calculated in a certain way by adding or multiplying matrices together.

Matrices are a key concept in linear algebra and appear in almost all areas of mathematics. They clearly represent relationships in which linear combinations play a role and thus facilitate calculation and thought processes. In particular, they are used to represent linear mappings and to describe and solve systems of linear equations. The term matrix was introduced in 1850 by James Joseph Sylvester.

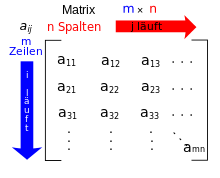
An arrangement, as in the adjacent figure, of $m \cdot n$ elements $a_{ij}\,$ is in rows and columns. The generalization to more than two indices is also called a hypermatrix.

Designations

Scheme for a general $m\times n$ matrix

Terms and first properties

Notation

As notation, the arrangement of the elements in rows and columns between two large opening and closing brackets has become established. As a rule, round brackets are used, but square brackets are also used. For example

${\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{pmatrix}}$ and ${\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{bmatrix}}$

Matrices with two rows and three columns. Matrices are usually denoted by capital letters (sometimes bolded or, handwritten, single or double underlined), preferably , denoted. A matrix with rows and columns:

$A={\boldsymbol {A}}={\underline {A}}={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &&\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}=(a_{ij})_{i=1,\dotsc ,m;\ j=1,\dotsc ,n}$ .

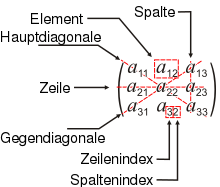
Elements of the matrix

The elements of the matrix are also called entries or components of the matrix. They originate from a set usually a body or a ring. One speaks of a matrix over . If one chooses for the set of real numbers, one speaks of a real matrix, for complex numbers of a complex matrix.

A given element is described by two indices, usually the element in the first row and the first column is described by $a_{11}$ . Generally, $a_{ij}$ denotes the element in the -th row and the -th column. When indexing, the row index is always named first and the column index second. Rule of thumb: row first, column later. If there is a danger of confusion, the two indices are separated by a comma. For example, the matrix element in the first row and the eleventh column is named . $a_{1,11}$

Individual rows and columns are often referred to as column or row vectors. Example:

$A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix},$ here $\begin{pmatrix} a_{11} \\ a_{21} \end{pmatrix}$ and $\begin{pmatrix} a_{12} \\ a_{22} \end{pmatrix}$ the columns or column vectors and $\begin{pmatrix} a_{11} & a_{12} \end{pmatrix}$ and $\begin{pmatrix} a_{21} & a_{22} \end{pmatrix}$ the rows or row vectors.

For singly standing row and column vectors of a matrix, the invariant index is occasionally omitted. Sometimes column vectors are written as transposed row vectors for more compact representation, thus:

$\begin{pmatrix} a_{11} \\ a_{21} \end{pmatrix}$ or ${\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}$ as ${\begin{pmatrix}a_{11}&a_{21}\end{pmatrix}}^{T}$ or ${\begin{pmatrix}a_{1}&a_{2}\end{pmatrix}}^{T}$

Type

The type of a matrix is determined by the number of its rows and columns. A matrix with rows and columns is called an $m\times n$ matrix (speak: m-by-n or m-cross-n matrix). If the number of rows and columns match, it is called a square matrix.

A matrix consisting of only one column or only one row is usually considered a vector. A vector with elements can be represented as a single-column $n \times 1$ matrix or a single-line $1 \times n$ matrix, depending on the context. In addition to the terms column vector and row vector, the terms column matrix and row matrix are common for this. A $1\times 1$ matrix is both a column and row matrix and is considered a scalar.

Formal representation

A matrix is a doubly indexed family. Formally this is a function

$A\colon \{1,\dotsc ,m\}\times \{1,\dotsc ,n\}\to K,\quad (i,j)\mapsto a_{ij},$

which assigns to each index pair (i,j) as function value the entry $a_{ij}$ . For example, the index pair (1,2) is assigned as a function value the entry $a_{12}$ . Thus, the function value $a_{ij}$ is the entry in the -th row and the -th column. The variables and correspond to the number of rows and columns, respectively. Not to be confused with this formal definition of a matrix as a function is that matrices themselves describe linear mappings.

The set $\operatorname {Abb} \left(\{1,\dotsc ,m\}\times \{1,\dotsc ,n\},K\right)$ of all $m\times n$ -matrices over the set is also called in usual mathematical notation $K^{\{1,\dotsc ,m\}\times \{1,\dotsc ,n\}}$ ; for this, the shorthand notation $K^{m\times n}$ common. Sometimes the notations $K^{m,n},$ $M(m \times n, K)$ or more rarely ${}^{m}K^{n}$ used.

Addition and multiplication

Elementary arithmetic operations are defined on the space of matrices.

Matrix addition

→ Main article: Matrix addition

Two matrices can be added if they are of the same type, that is, if they have the same number of rows and the same number of columns. The sum of two $m\times n$ matrices is defined componentwise:

$A+B:=(a_{ij}+b_{ij})_{i=1,\dotsc ,m;\ j=1,\dotsc ,n}$

Calculation example:

${\begin{pmatrix}1&-3&2\\1&2&7\end{pmatrix}}+{\begin{pmatrix}0&3&5\\2&1&-1\end{pmatrix}}={\begin{pmatrix}1+0&-3+3&2+5\\1+2&2+1&7+(-1)\end{pmatrix}}={\begin{pmatrix}1&0&7\\3&3&6\end{pmatrix}}$

In linear algebra, the entries of the matrices are usually elements of a body, such as the real or complex numbers. In this case, the matrix addition is associative, commutative, and has a neutral element in the form of the zero matrix. In general, however, the matrix addition has these properties only if the entries are elements of an algebraic structure that has these properties.

Scalar multiplication

→ Main article: Scalar multiplication

A matrix is multiplied by a scalar by multiplying each entry of the matrix by the scalar:

$\lambda \cdot A:=(\lambda \cdot a_{ij})_{i=1,\dotsc ,m;\ j=1,\dotsc ,n}$

Calculation example:

$5\cdot {\begin{pmatrix}1&-3&2\\1&2&7\end{pmatrix}}={\begin{pmatrix}5\cdot 1&5\cdot (-3)&5\cdot 2\\5\cdot 1&5\cdot 2&5\cdot 7\end{pmatrix}}={\begin{pmatrix}5&-15&10\\5&10&35\end{pmatrix}}$

Scalar multiplication must not be confused with scalar product. To be allowed to perform scalar multiplication, the scalar λ $\lambda$ (lambda) and the entries of the matrix must $(K,+,\cdot,0)$ come from the same ring The set of $m\times n$ -matrices in this case is a (left) module over

Matrix multiplication

→ Main article: Matrix multiplication

Two matrices can be multiplied if the number of columns of the left matrix is equal to the number of rows of the right matrix. The product of a $l \times m$ matrix $A=(a_{ij})_{i=1,\dotsc ,l,\;j=1,\dotsc ,m}$ and an $m\times n$ matrix $B=(b_{ij})_{i=1,\dotsc ,m,\;j=1,\dotsc ,n}$ is an $l \times n$ matrix $C=(c_{ij})_{i=1,\dotsc ,l,\;j=1,\dotsc ,n},$ whose entries are computed by applying the product sum formula, similar to the scalar product, to pairs of a row vector of the first matrix and a column vector of the second matrix:

$c_{ij}=\sum _{k=1}^{m}a_{ik}\cdot b_{kj}$

Matrix multiplication is not commutative, i.e., in general $B \cdot A \neq A \cdot B$ . However, matrix multiplication is associative, i.e., it always holds:

$(A \cdot B) \cdot C = A \cdot (B \cdot C)$

Therefore, a chain of matrix multiplications can be parenthesized in different ways. The problem of finding a bracketing that leads to a computation with the minimum number of elementary arithmetic operations is an optimization problem. Moreover, matrix addition and matrix multiplication satisfy both distributive laws:

$(A + B) \cdot C = A \cdot C + B \cdot C$

for all $l \times m$ -matrices A,B and $m\times n$ -matrices as well as

$A \cdot (B + C) = A \cdot B + A \cdot C$

for all $l \times m$ matrices and $m\times n$ matrices B, C.

Quadratic matrices $A\in K^{n\times n}$ can be multiplied by themselves, analogous to the power in real numbers one introduces abbreviatively the matrix power $A^2=A\cdot A$ or $A^3=A\cdot A\cdot A$ . Thus it is also useful to insert square matrices as elements in polynomials. For further discussion on this, see Characteristic Polynomial. For simpler computation, the Jordan normal form can be used here. Quadratic matrices over $\mathbb {R}$ or $\mathbb {C}$ can even be used in power series, cf. matrix exponential. A special role with respect to matrix multiplication is played by the square matrices over a ring , that is, $R^{n\times n}$ . These themselves, with matrix addition and multiplication, in turn form a ring called a matrix ring.