Transitive relation

This article or subsequent section is not sufficiently supported by evidence (e.g. itemised). Information without sufficient evidence may be removed in the near future. Please help Wikipedia by researching the information and adding good supporting evidence.

A transitive relation in mathematics is a two-digit relation on a set that has the property that for three elements , this set yRz always xRz follows from xRy and . Examples of transitive relations are the equal and the less relations on the real numbers, because for three real numbers , and with x=y and always also $y=z$ holds. $x=z$ and from x < y < z $y<z$ {\displaystyle x<z}

A non-transitive relation is called intransitive (not to be confused with negative transitivity). Transitivity is one of the prerequisites for an equivalence relation or an order relation.

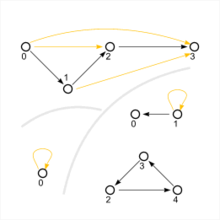
Two transitive and one non-transitive relation (bottom right), shown as directed graphs

Formal definition

If a set and $R\subseteq M\times M$ two-digit relation on then is called transitive if (using infix notation) holds:

$\forall x,y,z\in M:xRy\land yRz\Rightarrow xRz.$

Representation as a directed graph

Any relation on a set can be understood as a directed graph (see example above). The nodes of the graph are the elements of . A directed edge (an arrow $a\longrightarrow b$ ) is drawn from node to node aRb holds.

The transitivity of can now be characterised in the graph in this way: Whenever two arrows follow each other ( $a\longrightarrow b\longrightarrow c$ ), there is also an arrow that directly connects the initial and final nodes ( $a\longrightarrow c$ ) (so also in the Hasse diagram).

Properties

The transitivity of a relation also allows inferences across several steps (as is easily shown by complete induction):

$a\,R\,b_{1}\,R\,b_{2}\,R\,\dots \,R\,b_{n}\,R\,c\implies a\,R\,c$

With the help of the concatenation $\circ$ of relations, transitivity can also be characterised by the following condition:

$R\circ R\subseteq R$

If the relation transitive, then this is also true for the converse relation $R^{-1}$ . Examples: the relation that is converse to ≤ {\displaystyle $\leq$ ≥ $\geq$ which is converse $<\$ to is > {\displaystyle
If the relations and are transitive, then this is also true for their intersection $R\cap S$ . This statement can be generalised from two relations to the average $\cap _{{i\in I}}R_{i}$ any family of transitive relations.
For any relation is a smallest transitive relation which contains , the so-called transitive hull of .
Example: Let be the antecedent relation on the set of natural numbers, so let $a\,R\,b:\Longleftrightarrow a=b-1$ . The relation itself is not transitive. As a transitive envelope of the smaller relation results.

Examples

Order of the real numbers

The lessor relation $<\$ real numbers is transitive, because from x < y x<y y<z a strict total order.

Likewise, the relations $>\$ , ≤ $\leq \$ and ≥ $\geq \$ transitive.

Equality of the real numbers

The ordinary equality $=\$ on the real numbers is transitive, because from x=y and y=z follows x=z . Furthermore, it is an equivalence relation.

The inequality relation $\neq$ on the real numbers, on the other hand, is not transitive: $3\neq 5$ and $5\neq 3$ but $3\neq 3$ does not apply, of course.

Divisibility of the integers

The divisibility relation for integers is transitive, because from a|b and b|c follows a|c . Moreover, it is a quasi-order. When restricting to the set of natural numbers, one obtains a half-order.

For example, the divisor strangeness is not transitive. Thus and are alien to the divisor, as are and but and have the common divisor .

Subset

The subset relation $\subseteq$ between sets is transitive, because from $A\subseteq B$ and $B\subseteq C$ follows $A\subseteq C$ . Furthermore, $\subseteq$ a half-order.

For example, the disjointness of sets is not transitive. Thus the sets $\lbrace 1,2\rbrace$ and are $\lbrace 3\rbrace$ disjoint, as are $\lbrace 3\rbrace$ and $\lbrace 1,4\rbrace$ , but not $\lbrace 1,2\rbrace$ and $\lbrace 1,4\rbrace$ (since they have element 1 in common).

Parallel straight lines

In geometry, the parallelism of lines is transitive: if both the lines $g_{1}$ and $g_{2}$ parallel and the lines $g_{2}$ and $g_{3}$ then $g_{1}$ and $g_{3}$ are also parallel. Furthermore, parallelism is an equivalence relation.

Implication in logic

In logic, transitivity applies with regard to implication, although in predicate logic this is also known as modus barbara:

From $A \Rightarrow B$ and $B\Rightarrow C$ follows $A\Rightarrow C$ (compare also: cutting rule).

The implication defines a quasi-order on the formulae of the logic under consideration.

From a > b and b > c follows a > c