Geometric transformation

In a coordinate transformation, the coordinates of a point in one coordinate system are used to calculate its coordinates in another coordinate system. Formally, this is the transformation (transformation) of the original coordinates {\displaystyle (x_{1},x_{2},\dotsc ,x_{n})}into the new coordinates {\displaystyle (x'_{1},x'_{2},\dotsc ,x'_{n})}. The most common applications are in geometry, geodesy, image measurement, and engineering tasks, but also in such popular areas as computer animation or computer games, where the depicted "reality" must be continuously recomputed from the player's point of view (as a moving coordinate system).

Typical coordinate transformations occur through rotation, scaling, shearing and translation of the coordinate system, which can also be combined.

In general, the new coordinates can be x'_iarbitrary functions of the old coordinates x_{i}. Usually one uses special transformations where these functions are subject to certain constraints - e.g. differentiability, linearity or shape fidelity. Coordinate transformations can be used when a problem can be solved more easily in a different coordinate system, for example, when transforming Cartesian coordinates to spherical coordinates or vice versa.

A special case of the coordinate transformation is the base change in a vector space.

The transformations considered here, in which the coordinate systems are changed and thus only the coordinates of the points change, while the points themselves remain unchanged, are also called passive or alias transformations, while transformations in which conversely the position of the points changes with respect to a fixed coordinate system are also called active or alibi transformations (see Fig.).

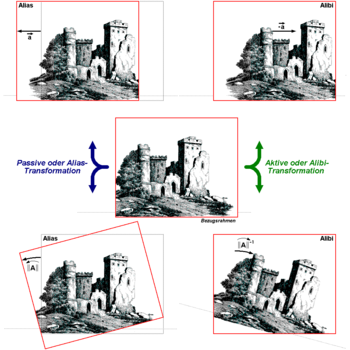
Coordinate transformation with object assumed to be at rest (left) or coordinate system assumed to be at rest (right)Zoom
Coordinate transformation with object assumed to be at rest (left) or coordinate system assumed to be at rest (right)

Linear transformations

See also: Linear mapping

In linear transformations, the new coordinates are linear functions of the original ones, i.e.

x'_1 = a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n

x'_2 = a_{21} x_1 + a_{22} x_2 + \dots + a_{2n} x_n

\ldots

{\displaystyle x'_{n}=a_{n1}x_{1}+a_{n2}x_{2}+\dots +a_{nn}x_{n}}.

This can be compactly represented as a matrix multiplication of the old coordinate vector \vec{x} = (x_1, \dots, x_n)with the matrix Aa_{ij}containing the coefficients

{\displaystyle {\vec {x}}'=A{\vec {x}}}.

The origin of the new coordinate system coincides with that of the original coordinate system.

Rotation

An important type of linear coordinate transformations are those in which the new coordinate system is rotated around the origin of the coordinates (the so-called "alias transformation" in the adjacent graphic). In two dimensions, the only parameter is the angle of rotation; in three dimensions, on the other hand, an axis of rotation that is not changed by the rotation must also be defined. The rotation is described in both cases by a rotation matrix.

Example

Consider two three-dimensional Cartesian coordinate systems Sand S'with a common z-axis and common origin. Let the coordinate system S'be rotated clockwise about the z-axis\varphi with respect to Sby an angleA point P that {\displaystyle {\vec {x}}=(x,y,z)}has coordinates the coordinate system S then has coordinates the coordinate system S' {\displaystyle {\vec {x}}'=(x',y',z')}with:

{\displaystyle x'=+x\cos \varphi -y\sin \varphi ,}

{\displaystyle y'=+x\sin \varphi +y\cos \varphi ,}

z'=z.

In matrix notation, the inverse rotation matrix for this rotation of the coordinate system gives:

{\displaystyle {\vec {x}}'={\begin{pmatrix}\cos \varphi &-\sin \varphi &0\\\sin \varphi &\cos \varphi &0\\0&0&1\end{pmatrix}}{\vec {x}}.}

Scaling

Scaling changes the "units" of the axes. That is, the numerical values of the coordinates x_{i}are \lambda _{i}multiplied ("scaled") by constant factors λ

x_i'=\lambda_i\cdot x_i.

The parameters of this transformation are the NNumbers λ \lambda _{i} . A special case is the "scale transformation" where all factors have the same value

\lambda_i=\lambda.

The matrix Ain this case is λ \lambda times the unit matrix.

Shear

During shear, the angle between the coordinate axes changes. Therefore, in two dimensions there is one parameter, and in three-dimensional space - three parameters.

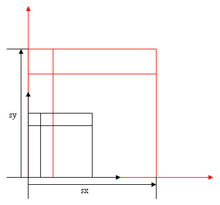
ScalingZoom
Scaling

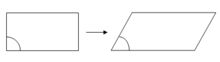
ShearZoom
Shear

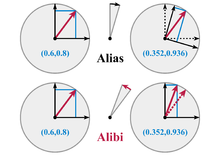
Rotation of a coordinate system with respect to a vector considered to be at rest and of a vector with respect to a coordinate system considered to be at restZoom
Rotation of a coordinate system with respect to a vector considered to be at rest and of a vector with respect to a coordinate system considered to be at rest

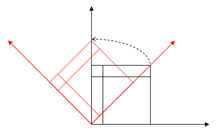
Counterclockwise rotation of the coordinate systemZoom
Counterclockwise rotation of the coordinate system

Affine transformations

See also: Affine mapping

Affine transformations consist of a linear transformation and a translation.

If both coordinate systems involved are linear, (i.e. in principle given by a coordinate origin and uniformly subdivided coordinate axes), then an affine transformation is present. Here the new coordinates are affine functions of the original ones, thus

x'_1 = a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n + b_1

x'_2 = a_{21} x_1 + a_{22} x_2 + \dots + a_{2n} x_n + b_2

\ldots

{\displaystyle x'_{n}=a_{n1}x_{1}+a_{n2}x_{2}+\dots +a_{nn}x_{n}+b_{n}}

This can be compactly written as matrix multiplication of the old coordinate vector \vec{x} = (x_1, \dots, x_n)with the matrix A, containing the coefficients a_{ij}, and adding a vector {\displaystyle \vec{b}containing the b_{i}

\vec{x}\,'=A \vec{x} + \vec{b}

The translation is a special case of an affine transformation where A is the unit matrix.

Displacement (Translation)

Two coordinate systems Sand are consideredS'. The system S'is \vec{b}shifted with respect to Sby the vector A point which P{\vec {x}}has coordinates Sin the coordinate system , then has coordinates the coordinate system S'{\displaystyle {\vec {x}}'={\vec {x}}-{\vec {b}}}.

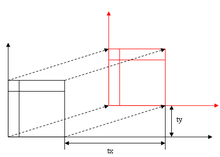
PostponementZoom
Postponement


AlegsaOnline.com - 2020 / 2023 - License CC3