Torus

The title of this article is ambiguous. For other meanings, see Torus (disambiguation).

A torus (plural tori, from Latin torus) is a mathematical object from geometry and topology. It is a bead-like shaped surface with a hole, so it has the shape of a tennis ring, also life ring, hoop or donut.

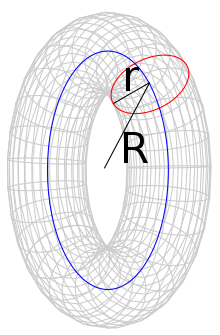
Examples of tori embedded in three-dimensional space are the rotation tori. Rotation tori are surfaces of rotation that are obtained by rotating a circle around an axis that lies in the plane of the circle and does not intersect the circle. If you rotate not only the circle line, but the whole circle surface, you get a full torus.

In other words, a rotation torus is formed from that set of points which fixed distance with from a circular line of radius R r<R

A torus can also be constructed by identifying the sides of a parallelogram. In this case, the right edge of the parallelogram is connected to its left edge and the top edge is connected to the bottom edge. This topology is also used by many computer games: If a game object leaves the playing field on one side, it reappears on the opposite side.

Both constructions are special cases of the general mathematical definition, which defines a torus as the topological product of two circles. This notion plays a role in numerous areas of mathematics, besides topology and differential geometry, it is important in Fourier analysis, the theory of dynamical systems (invariant tori in celestial mechanics), the theory of functions and the theory of elliptic curves, among others.

Rotation tori provide a concrete rotationally symmetric realization of this surface in three-dimensional Euclidean space. Significant for many applications in theoretical mathematics and physics is another embedding as a flat torus in four-dimensional space. This has the curvature zero and the maximum possible symmetry.

The torus is a two-dimensional surface. More generally, in mathematics one also considers the , a -dimensional manifold generalizing the two-dimensional torus. Deviating from this, in the German-language literature occasionally also the terms Doppeltorus, Tripeltorus etc. are used for surfaces with two, three and more holes.

Torus

The torus is obtained by gluing opposite sides of a parallelogram together

The set of points with distance from the circle line with radius form a rotation torus.

Volume

The volume of the torus can be calculated as a volume integral over the Jacobi determinant (the determinant of the functional matrix). The Jacobi matrix for the parametrization of the torus can be given as follows:

$J_{f}={\frac {\partial \left(x,y,z\right)}{\partial \left(r,t,p\right)}}={\begin{pmatrix}\partial _{r}x&\partial _{t}x&\partial _{p}x\\\partial _{r}y&\partial _{t}y&\partial _{p}y\\\partial _{r}z&\partial _{t}z&\partial _{p}z\\\end{pmatrix}}={\begin{pmatrix}\cos(t)\cos(p)&-R\sin(t)-r\sin(t)\cos(p)&-r\cos(t)\sin(p)\\\sin(t)\cos(p)&R\cos(t)+r\cos(t)\cos(p)&-r\sin(t)\sin(p)\\\sin(p)&0&r\cos(p)\end{pmatrix}}$

It follows:

$\det(J_{f})=r\cdot \left(r\cos(p)+R\right)$

Thus, the functional determinant here is equal to the norm of the surface normal vector.

$V=\int _{V}\mathrm {d} V=\int _{\Gamma }\det(J_{f})\ \mathrm {d} \Gamma =\int _{0}^{2\pi }\int _{0}^{2\pi }\int _{0}^{r}\left(Rr+r^{2}\cos(p)\right)\ \mathrm {d} r\ \mathrm {d} p\ \mathrm {d} t=2\pi ^{2}r^{2}R$

Thus, we obtain for the volume of the solid torus $V=2\pi ^{2}r^{2}R$ .

The formula for the volume can be interpreted as $U_{R}=2\pi R$ multiplying the circular area $A_{r}=\pi r^{2}$ by the circumference (see Second Guldin's Rule). This can be put in analogy to the cylinder volume $V_{\text{zyl}}=\pi r^{2}l$ understanding. It is the same with the surface area, here the perimeters $U_{r}=2\pi r$ and $U_{R}=2\pi R$ multiplied together (see First Guldin's Rule). This is also analogous to the cylinder surface $O_{\text{zyl}}=2\pi rl$ .

Considering only the inner part of the torus, which has a distance from the axis is less than or equal to , we get the volume

$\int _{0}^{2\pi }\int _{\tfrac {\pi }{2}}^{\tfrac {3\pi }{2}}\int _{0}^{r}\left(Rr+r^{2}\cos(p)\right)\ \mathrm {d} r\ \mathrm {d} p\ \mathrm {d} t=\pi r^{2}\left(\pi R-{\tfrac {4r}{3}}\right)$

The outer part of the torus, which has a distance from the axis has a distance greater than or equal to , has the volume

$\int _{0}^{2\pi }\int _{\tfrac {3\pi }{2}}^{\tfrac {\pi }{2}}\int _{0}^{r}\left(Rr+r^{2}\cos(p)\right)\ \mathrm {d} r\ \mathrm {d} p\ \mathrm {d} t=\pi r^{2}\left(\pi R+{\tfrac {4r}{3}}\right)$

Surface

The surface of the torus with the above parameter representation is

$A_{O}=4\pi ^{2}rR$

This formula can be derived either with Guldin's First Rule from

$A_{O}=2\pi r\cdot 2\pi R$

or with the help of the surface integral

$A_{O}=\iint \mathrm {d} A=\int _{t=0}^{2\pi }\int _{p=0}^{2\pi }r(R+r\cos(p))\ \mathrm {d} p\ \mathrm {d} t$

calculate. Here $\mathrm {d} A=r(R+r\cos(p))\ \mathrm {d} p\ \mathrm {d} t$ the surface element of the torus in the parameter representation above.

The torus bounds a 3-dimensional solid torus. The volume of the solid torus is $V=2\pi ^{2}r^{2}R$ (see Second Guldin's Rule).

Considering only the inner part of the torus, which has a distance from the axis is less than or equal to , we get the surface

$\int _{t=0}^{2\pi }\int _{p={\tfrac {\pi }{2}}}^{\tfrac {3\pi }{2}}r(R+r\cos(p))\ \mathrm {d} p\ \mathrm {d} t=2\pi r\left(\pi R-2r\right)$

The outer part of the torus, which has a distance from the axis has a distance greater than or equal to , has the surface

$\int _{t=0}^{2\pi }\int _{p={\tfrac {3\pi }{2}}}^{\tfrac {\pi }{2}}r(R+r\cos(p))\ \mathrm {d} p\ \mathrm {d} t=2\pi r\left(\pi R+2r\right)$

Torus as surface of revolution

A rotation torus is a surface of revolution created by rotating a circle about an axis of rotation lying in the plane of the circle and not intersecting the circle. A rotation torus can be described as the set of points that are a fixed distance from a circular line of radius , where In Cartesian coordinates x,y,z , with the z-axis as the axis of rotation and the centers of the rotating circle in the x-y plane, it is given by Eq.

$\left({\sqrt {x^{2}+y^{2}}}-R\right)^{2}+z^{2}=r^{2}$

is described. Eliminating the root yields the 4th degree equation

$\left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y^{2}\right).$

One can introduce in the torus surface a toroidal coordinate and a poloidal coordinate perpendicular to it. The torus is thought of as being created by a circle rotated about an axis lying in the plane of the circle. We call the radius of the original circle , this circle also simultaneously forms a coordinate line of . The distance of the center of the circle from the axis we call , the coordinate lines of are circles around the axis of rotation. Both coordinates are angles and run from $0$ to $2\pi$ .

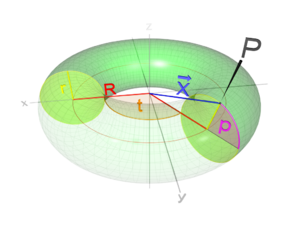
Parameterization

The conversion of torus coordinates into Cartesian coordinates is

${\begin{pmatrix}x\\y\\z\end{pmatrix}}=R\cdot {\begin{pmatrix}\cos(t)\\\sin(t)\\0\end{pmatrix}}+r\cdot {\begin{pmatrix}\cos(t)\cdot \cos(p)\\\sin(t)\cdot \cos(p)\\\sin(p)\end{pmatrix}}={\begin{pmatrix}(R+r\cdot \cos(p))\cos(t)\\(R+r\cdot \cos(p))\sin(t)\\r\cdot \sin(p)\end{pmatrix}}$

Torus coordinates are important in nuclear fusion technology, see nuclear fusion reactor.

Plane cuts

Intersections with planes containing the axis of rotation are pairs of circles.
Intersections with planes perpendicular to the axis of rotation are pairs of circles or a circle or empty.
A plane parallel to the axis of rotation cuts out a spiral curve from a torus. In special cases this can be a Cassinian curve.
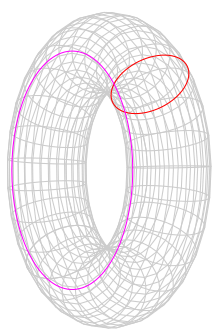
An inclined plane touching two generating circles cuts out Villarceau circles.

Tori in descriptive geometry

In descriptive geometry, parts of a torus are used to construct transition surfaces between cylinders. The representation of a torus by its outline is found in outline constructions.

A radial ...

... and diagonally sliced torus in 3D

General definition

Let $\mathbb {S} ^{1}$ is the circle (the 1-sphere). The -torus is then defined by

$\mathbb {T} ^{n}:=\underbrace {\mathbb {S} ^{1}\times \cdots \times \mathbb {S} ^{1}} _{n\ {\text{mal}}}$ ,

where $\times$ is the product of topological spaces. The surface of revolution described in the previous section is a 2-torus. The 2-torus is usually simply called a torus.

The 2-dimensional torus as a product of two circles.

Topological properties

Structure of a manifold

The -torus is a topological manifold. This follows from the fact that the -torus is the topological product of 1-spheres and the 1-sphere itself is a topological manifold. In addition, the 1-sphere is also a differentiable manifold and, since the product of differentiable manifolds again gives a differentiable manifold, the -torus is also a differentiable manifold. The dimension of $\mathbb {T} ^{n}$ is equal to .

Topological properties

It also follows directly from the definition that the -torus is compact. Moreover, it is path coherent. Unlike the -sphere, the for n>1 simply connected.

The mapping $q\colon \mathbb {R} ^{n}\to \mathbb {T} ^{n}$ , defined by $(x_{j})_{j}:=(\exp(2\pi \mathrm {i} x_{j}))_{j}$ , is the universal superposition of the -torus.

Lie Group

The 1-sphere, conceived as a circle group, is also a Lie group. Since the product of several Lie groups with the componentwise multiplication is again a Lie group, the -torus is also a Lie group.

Embedded tori

Flat tori

Since the circle line $\mathbb {S} ^{1}$ obviously can be embedded in the $\mathbb {R} ^{2}$ embedded, the -torus $\mathbb {T} ^{n}:=\mathbb {S} ^{1}\times \cdots \times \mathbb {S} ^{1}\subset \mathbb {R} ^{2n}$ as a subset of the Euclidean space $\mathbb {R} ^{2n}$ can be conceived. One considers on $\mathbb {T} ^{n}$ the Riemannian metric , which is given by the Euclidean metric of the space $\mathbb {R} ^{2n}$ on the -torus is induced. This metric is flat, that is, the is locally isometric to a neighborhood of the $\mathbb {R} ^{n}$ . In particular, therefore, its sectional curvature is everywhere constant zero. Since the -torus is compact and hence complete, it is a flat manifold. Therefore it is also called a flat -torus.

There are other flat metrics on the torus besides the one described above. Flat 2-tori can be described by a parallelogram whose opposite sides are glued together. Equivalently, flat tori can be described as topological factor groups $\mathbb {R} ^{2}/(\mathbb {Z} \cdot v+\mathbb {Z} \cdot w)$ for two linearly independent vectors $v,w\in \mathbb {R} ^{2}$ can be described. In the special case v=(1,0) and w=(0,1) we obtain the quotient $\mathbb {R} ^{2}/\mathbb {Z} ^{2}\cong (\mathbb {R} /\mathbb {Z} )^{2}$ .

Elliptic curves over the complex numbers can be represented by Weierstrass parametrization as $\mathbb {C} /L$ for a lattice $L\subset \mathbb {C}$ and are thus (with a translation invariant metric) examples of flat tori. The moduli space of elliptic curves or equivalently of flat 2-tori is the so-called moduli curve.

Flat tori in three-dimensional space

A 2-times differentiable embedding of the torus into the three-dimensional space cannot be flat, because the local extrema must be points of positive curvature. However, according to Nash's embedding theorem, there are fractal (only 1 times differentiable) embeddings of the flat torus into the three-dimensional space. These can also be constructed numerically.

Rotation tori in three-dimensional space

A rotation torus is a 2-torus embedded in $\mathbb {R} ^{3}$ embedded 2-torus, which can be described as the set of points that have fixed distance from a circular line of radius , where

Clifford-Tori

A Clifford torus is a special torus embedded in $S^{3}\subset \mathbb {R} ^{4}$ embedded torus. After identifying $\mathbb {R} ^{4}=\mathbb {C} ^{2}$ and $S^{3}=\left\{(z,w)\in \mathbb {C} ^{2}\colon |z|^{2}+|w|^{2}=1\right\}$ , the standard Clifford torus can be described as.

$T:=\left\{(z,w)\in \mathbb {C} ^{2}\colon |z|=|w|={\frac {1}{\sqrt {2}}}\right\}\subset S^{3}$ .

Furthermore, the images of under isometries of the standard metric $A\in O(3)=\operatorname {Isom} (S^{3})$ called Clifford-Tori.

Using stereographic projection, Clifford tori can also be thought of as tori embedded in the $\mathbb {R} ^{3}$ embedded tori.

A Clifford torus is a minimal surface with respect to the standard metric on the $S^{3}$ . The Lawson conjecture proved by Brendle states that any $S^{3}$ torus embedded as a minimal surface in the is a Clifford torus.

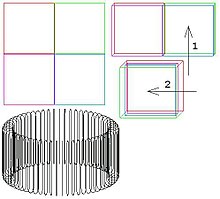
Model of a flat torus: The paper only needs to be bent, not stretched.

Construction from a square or cube

Construction of two-dimensional tori from a square or parallelogram

Unlike the surface of a sphere, the torus can be mapped onto a flat rectangular surface without singularities.

Here, the right edge of the rectangle or square is stitched to its left edge, and its bottom edge is stitched to its top edge. This construction also works with any parallelogram. Many computer games, for example Asteroids or Pac-Man, also have this topology: If a game object leaves the playing field on one side, it reappears on the opposite side.

Construction of higher dimensional tori from a cube or parallelepiped

The three-dimensional torus or 3-torus is a parallelepiped or cube whose six opposite faces are interlocked in pairs.

The four-dimensional torus or 4-torus is a tesseract whose eight opposing cubes are interlocked in pairs.

In general, the -dimensional torus is an -dimensional cube $[0,1]^{n}$ , whose opposite (n-1) -hypercubes are pairwise identified with each other. It can also be written as $\mathbb {R} ^{n}/\mathbb {Z} ^{n}$ .

Again, instead of an -dimensional cube, one can use any -dimensional parallelepiped to construct an torus by identifying the sides.

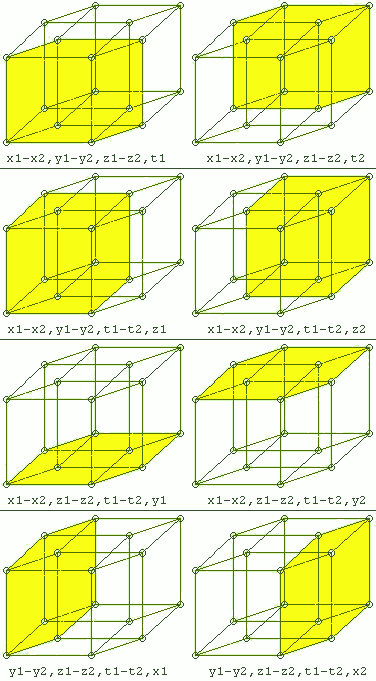
Features of the 3-Torus

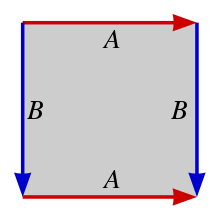
The torus is obtained from a square by gluing opposite sides.

Seven-color set

The seven-color theorem for the torus states that 7 colors are always sufficient to color any map on the surface of a torus so that no two adjacent countries get the same color.

This means that any graph that can be embedded in the torus has a chromatic number of at most 7 (see node coloring). Because the complete graph $K_{7}$ can be embedded in the torus, the chromatic number is equal to 7.

In the plane or on a spherical surface, fewer colors are sufficient. The four-color theorem states that four colors are always sufficient to color any map in the Euclidean plane in such a way that no two adjacent countries get the same color.

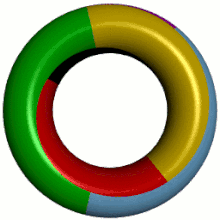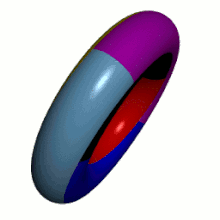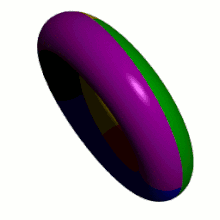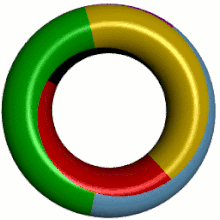
Animation of a torus. The surface is divided into 7 areas with different colors.

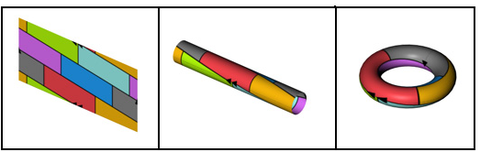
The surface of a torus can be divided into 7 areas in such a way that two areas touch each other. Therefore, in order to color this map so that no two adjacent areas get the same color, 7 colors are needed.

Algebraic torus

In the theory of algebraic groups torus is used in a different sense. There it means a group which is isomorphic to a finite product of copies of the multiplicative group of a body. To distinguish it, one then speaks of an algebraic torus in contrast to a topological torus.

For example, in toric geometry, the study of toric varieties, a torus is usually an algebraic torus.

Application examples

A life ring with outer diameter 76 centimeters and inner diameter 44 centimeters has the shape of a torus. It therefore has a fixed distance $r=(76\ \mathrm {cm} -44\ \mathrm {cm} )/4=8\ \mathrm {cm}$ from a circular line with radius $R=(76\ \mathrm {cm} +44\ \mathrm {cm} )/4=30\ \mathrm {cm}$ .

This results in the volume and the surface area:

Volume: $V=2\cdot \pi ^{2}\cdot r^{2}\cdot R=2\cdot \pi ^{2}\cdot (8\ \mathrm {cm} )^{2}\cdot 30\ \mathrm {cm} \approx 37899\ \mathrm {cm^{3}} =0{,}037899\ \mathrm {m^{3}}$

Surface: $A_{O}=4\cdot \pi ^{2}\cdot r\cdot R=4\cdot \pi ^{2}\cdot 8\ \mathrm {cm} \cdot 30\ \mathrm {cm} \approx 9475\ \mathrm {cm^{2}} =0{,}9475\ \mathrm {m^{2}}$

A life ring has the shape of a torus.

Torus

Volume

Surface

Torus as surface of revolution

Parameterization

Plane cuts

Tori in descriptive geometry

General definition

Topological properties

Structure of a manifold

Topological properties

Lie Group

Embedded tori

Flat tori

Flat tori in three-dimensional space

Rotation tori in three-dimensional space

Clifford-Tori

Construction from a square or cube

Construction of two-dimensional tori from a square or parallelogram

Construction of higher dimensional tori from a cube or parallelepiped

Seven-color set

Algebraic torus

Application examples

See also

Search by letter