Torsion (mechanics)

Torsion describes the twisting of a body caused by the action of a torsional moment. If you try to twist a rod with a lever perpendicular to the longitudinal axis, a torsional moment acts on it (in addition to any transverse force).

The torsional moment results from the force on the lever multiplied by the length of the lever used for this purpose:

$T = F \cdot r$

The resulting twist (twist angle θ $\theta_t$ ) of the rod is given as:

${\begin{aligned}\theta _{t}&={\frac {T}{D}}\\&={\frac {T\cdot L}{G\cdot I_{T}}}\end{aligned}}$

with

Experimental setup for the determination of the torsion laws (wood engraving 1897)

Torsion of an angle iron (L-profile)

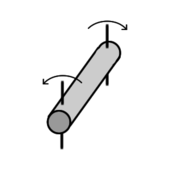
Illustration of the torsion

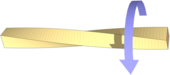
Torsion of a bar with a square cross section

Torsional moment of inertia

Exclusively for circular and for closed circular ring cross sections, the torsional moment of inertia is equal to the polar area moment of inertia I_p :

$I_{T}=I_{p}={\frac {r^{4}\cdot \pi }{2}}$

For other cross-sections, the calculation of the torsional moment of inertia is only possible in closed form in special cases.

In addition, when determining the torsional moment of inertia, it is often important to know whether the cross-sections are warp-free or not, and whether the warping is impeded or not.

Torsion without warping

For closed sections whose products of wall thickness and distance from the axis of rotation are constant laterally ( $r_{1}t_{1}=r_{2}t_{2}=\cdots =r_{m}t_{m}$ ), shear stresses are produced in the case of torsion, but no normal stresses in the longitudinal direction and thus no warping of the cross-section. These conditions are met, for example, by a cylindrical tube of constant wall thickness. This case of torsion is called Neuber's shell.

However, it should be noted that the linear elasticity theory applies, i.e. only small distortions and deformations are permitted, but no plastic deformations. In addition, the load should be applied in the form of the torsional moment on the longitudinal axis.

The shear stress τ ${\tau }_{t}$ in the member is given by the torsional moment divided by the polar section modulus $W_{p}$ :

$\tau_t = \frac{T}{W_p}$

The maximum shear stress occurs at the edge or at the maximum radius of the cross-section under consideration. When dimensioning, care must be taken to ensure that this shear stress does not exceed the maximum permissible shear stress τ $\tau_\mathrm{zul}$ of the material to be used:

$\tau \le \tau_\mathrm{zul}$

Otherwise, the deformation of a shaft, for example, passes from the elastic range into the plastic range and finally leads to fracture.

Questions and Answers

Q: What is torsion?

A: Torsion is the twisting of an object that results from an applied torque.

Q: How is shearing stress related to torsion?

A: In circular sections, the resultant shearing stress is perpendicular to the radius.

Q: What equation can be used to calculate shear stress at a point on a shaft?

A: The equation for calculating shear stress at a point on a shaft is τθz = Tr/J, where T is the applied torque, r is the distance from the center of rotation, and J is the polar moment of inertia.

Q: What equation can be used to find angle of twist?

A: The equation for finding angle of twist is θ = TL/JG, where L represents length and G represents modulus of rigidity.

Q: What does "T" represent in the equations for shear stress and angle of twist?

A: In both equations, "T" represents applied torque.

Q: What does "r" represent in the equation for shear stress?

A: In the equation for shear stress, "r" represents distance from center of rotation.

Q: What does "J" represent in both equations?

A:"J" represents polar moment of inertia in both equations.